Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T02:05:29.760Z Has data issue: false hasContentIssue false
  • English
  • Français

COMMON FIXED POINTS FOR SEMIGROUPS OF POINTWISE LIPSCHITZIAN MAPPINGS IN BANACH SPACES

Part of: Nonlinear operators and their properties

Published online by Cambridge University Press:  26 September 2011

W. M. KOZLOWSKI
W. M. KOZLOWSKI*
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, NSW 2052, Australia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

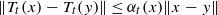Let C be a bounded, closed, convex subset of a uniformly convex Banach space X. We investigate the existence of common fixed points for pointwise Lipschitzian semigroups of nonlinear mappings Tt:C→C, where each Tt is pointwise Lipschitzian. The latter means that there exists a family of functions αt:C→[0,∞) such that for x,y∈C. We also demonstrate how the asymptotic aspect of the pointwise Lipschitzian semigroups can be expressed in terms of the respective Fréchet derivatives.

Keywords

fixed pointcommon fixed pointLipschitzian mappingpointwise Lipschitzian mappingpointwise contractionssemigroup of mappingsasymptotic pointwise nonexpansive mappinguniformly convex Banach spacestochastic dynamical systems

MSC classification

Secondary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 84 , Issue 3 , December 2011 , pp. 353 - 361
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

References

[1]Belluce, L. P. and Kirk, W. A., ‘Fixed-point theorems for families of contraction mappings’, Pacific J. Math. 18 (1966), 213–217.CrossRefGoogle Scholar
[2]Belluce, L. P. and Kirk, W. A., ‘Nonexpansive mappings and fixed-points in Banach spaces’, Illinois J. Math. 11 (1967), 474–479.CrossRefGoogle Scholar
[3]Browder, F. E., ‘Nonexpansive nonlinear operators in a Banach space’, Proc. Natl. Acad. Sci. USA 54 (1965), 1041–1044.CrossRefGoogle Scholar
[4]Bruck, R. E., ‘A common fixed point theorem for a commuting family of nonexpansive mappings’, Pacific J. Math. 53 (1974), 59–71.CrossRefGoogle Scholar
[5]Bruck, R. E., ‘A simple proof of the mean ergodic theorem for nonlinear contractions in Banach spaces’, Israel J. Math. 32 (1979), 107–116.CrossRefGoogle Scholar
[6]DeMarr, R. E., ‘Common fixed-points for commuting contraction mappings’, Pacific J. Math. 13 (1963), 1139–1141.CrossRefGoogle Scholar
[7]Hussain, N. and Khamsi, M. A., ‘On asymptotic pointwise contractions in metric spaces’, Nonlinear Anal. 71(10) (2009), 4423–4429.CrossRefGoogle Scholar
[8]Khamsi, M. A. and Kozlowski, W. K., ‘On asymptotic pointwise contractions in modular function spaces’, Nonlinear Anal. 73 (2010), 2957–2967.CrossRefGoogle Scholar
[9]Khamsi, M. A. and Kozlowski, W. K., ‘On asymptotic pointwise nonexpansive mappings in modular function spaces’, J. Math. Anal. Appl. 380 (2011), 697–708.CrossRefGoogle Scholar
[10]Kirk, W. A., ‘Mappings of generalized contractive type’, J. Math. Anal. Appl. 32 (1974), 567–572.CrossRefGoogle Scholar
[11]Kirk, W. A. and Xu, H. K., ‘Asymptotic pointwise contractions’, Nonlinear Anal. 69 (2008), 4706–4712.CrossRefGoogle Scholar
[12]Kozlowski, W. M., ‘Fixed point iteration processes for asymptotic pointwise nonexpansive mappings in Banach spaces’, J. Math. Anal. Appl. 377 (2011), 43–52.CrossRefGoogle Scholar
[13]Kozlowski, W. M., ‘On the existence of common fixed points for semigroups of nonlinear mappings in modular function spaces’, Comment. Math. 51(1) (2011), 81–98.Google Scholar
[14]Lim, T. C., ‘A fixed point theorem for families of nonexpansive mappings’, Pacific J. Math. 53 (1974), 487–493.CrossRefGoogle Scholar
[15]Tan, K.-K. and Xu, H.-K., ‘An ergodic theorem for nonlinear semigroups of Lipschitzian mappings in Banach spaces’, Nonlinear Anal. 19(9) (1992), 805–813.CrossRefGoogle Scholar
[16]Xu, H.-K., ‘Inequalities in Banach spaces with applications’, Nonlinear Anal. 16 (1991), 1127–1138.CrossRefGoogle Scholar