Article contents
Collections of sequences having the Ramsey property only for few colours
Published online by Cambridge University Press: 17 April 2009
Abstract
A family 𝑐 of sequences has the r-Ramsey property if for every positive integer k, there exists a least positive integer g(r)(k) such that for every r-colouring of {1, 2, …, g(r)(k)} there is a monochromatic k-term member of 𝑐. For fixed integers m > 1 and 0 ≤ a < m, define a k-term a (mod m)-sequence to be an increasing sequence of positive integers {x1, …, xk} such that xi − xi−1 ≡ a (mod m) for i = 2, …, k. Define an m-a.p. to be an arithmetic progression where the difference between successive terms is m. Let 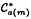 be the collection of sequences that are either a(mod m)-sequences or m-a.p.'s. Landman and Long showed that for all m ≥ 2 and 1 ≤ a < m,
be the collection of sequences that are either a(mod m)-sequences or m-a.p.'s. Landman and Long showed that for all m ≥ 2 and 1 ≤ a < m, 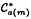 has the 2-Ramsey property, and that the 2-Ramsey function
has the 2-Ramsey property, and that the 2-Ramsey function 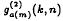 , corresponding to k-term a(mod m)-sequences or n-term m-a.p.'s, has order of magnitude mkn. We show that
, corresponding to k-term a(mod m)-sequences or n-term m-a.p.'s, has order of magnitude mkn. We show that 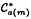 does not have the 4-Ramsey property and that, unless m/a = 2, it does not have the 3-Ramsey property. In the case where m/a = 2, we give an exact formula for
does not have the 4-Ramsey property and that, unless m/a = 2, it does not have the 3-Ramsey property. In the case where m/a = 2, we give an exact formula for 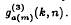 . We show that if a ≠ 0, there exist 4-colourings or 6-colourings (depending on m and a) of the positive integers which avoid 2-term monochromatic members of
. We show that if a ≠ 0, there exist 4-colourings or 6-colourings (depending on m and a) of the positive integers which avoid 2-term monochromatic members of 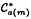 , but that there never exist such 3-colourings. We also give an exact formula for
, but that there never exist such 3-colourings. We also give an exact formula for 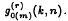 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1997
References
- 1
- Cited by


