Article contents
A class of modules over a locally finite group III
Published online by Cambridge University Press: 17 April 2009
Extract
Let G be a locally finite group, k a field of characteristic p ≥ 0 and V a right kG-module. We say that V is an 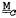 -module over kG, if each p′-subgroup H of G contains a finite subgroup F with the same fixed points as H in V. (By convention, 0′ is taken as the set of all primes.) Such modules arise as elementary abelian section of
-module over kG, if each p′-subgroup H of G contains a finite subgroup F with the same fixed points as H in V. (By convention, 0′ is taken as the set of all primes.) Such modules arise as elementary abelian section of 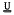 -groups, a class of locally finite groups similar in many ways to the class of finite soluble groups.
-groups, a class of locally finite groups similar in many ways to the class of finite soluble groups.
The main theorem is that if V is an 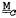 -module over kG with trivial Frattini submodule, and G is almost abelian, then every composition factor of V is complemented. This is a crucial ingredient in Tomkinson's theory of prefrattini subgroups in a certain subclass of
-module over kG with trivial Frattini submodule, and G is almost abelian, then every composition factor of V is complemented. This is a crucial ingredient in Tomkinson's theory of prefrattini subgroups in a certain subclass of 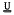 . An example is given to show that the theorem breaks down for metabelian G. This leads to an example of a
. An example is given to show that the theorem breaks down for metabelian G. This leads to an example of a 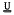 -group in which there are no analogues of prefrattini subgroups - the first situation where one of the standard conjugacy classes of subgroups of finite soluble groups has no decent analogue in the whole class
-group in which there are no analogues of prefrattini subgroups - the first situation where one of the standard conjugacy classes of subgroups of finite soluble groups has no decent analogue in the whole class 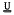
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 14 , Issue 1 , February 1976 , pp. 95 - 110
- Copyright
- Copyright © Australian Mathematical Society 1976
References
- 3
- Cited by


