Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T03:39:38.562Z Has data issue: false hasContentIssue false
  • English
  • Français

A CHARACTER-THEORETIC CRITERION FOR THE SOLVABILITY OF FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  20 January 2016

YAN-JUN LIU  and
YANG LIU
YAN-JUN LIU*
Affiliation:
College of Mathematics and Information Science, Jiangxi Normal University, Nanchang, PR China email [email protected]
YANG LIU
Affiliation:
Beijing International Center for Mathematical Research, Peking University, Beijing 100871, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 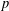$p$ be an odd prime. In this note, we show that a finite group 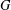$G$ is solvable if all degrees of irreducible complex characters of 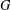$G$ not divisible by 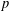$p$ are either 1 or a prime.

Keywords

finite groupirreducible charactersolvabilitycharacter degree

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20D05: Finite simple groups and their classification
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 30 - 35
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Berkovich, Y. G., ‘Degrees of irreducible characters and normal p-complements’, Proc. Amer. Math. Soc. 106 (1989), 33–34.Google Scholar
Bessenrodt, C., Balog, A., Olsson, J. B. and Ono, K., ‘Prime power degree representations of the symmetric and alternating groups’, J. Lond. Math. Soc. (2) 64 (2001), 344–356.Google Scholar
Bessenrodt, C. and Olsson, J. B., ‘Prime power degree representations of the double covers of the symmetric and alternating groups’, J. Lond. Math. Soc. (2) 66 (2002), 313–324.CrossRefGoogle Scholar
Bianchi, M., Chillag, D., Lewis, M. L. and Pacifici, E., ‘Character degree graphs that are complete graphs’, Proc. Amer. Math. Soc. 135 (2007), 671–676.CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of Finite Groups (Oxford University Press, Oxford, 1984).Google Scholar
Digne, F. and Michel, J., Representations of Finite Groups of Lie Type, London Mathematical Society Student Texts, 21 (Cambridge University Press, Cambridge, 1991).Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Isaacs, I. M. and Knutson, G., ‘Irreducible character degrees and normal subgroups’, J. Algebra 199 (1998), 302–326.Google Scholar
Kazarin, L. and Berkovich, Y., ‘On Thompson’s theorem’, J. Algebra 220 (1999), 574–590.CrossRefGoogle Scholar
Lewis, M. L. and White, D. L., ‘Connectedness of degree graphs of nonsolvable groups’, J. Algebra 266 (2003), 51–76.Google Scholar
Liu, Y. J. and Liu, Y., ‘Finite groups with exactly one composite character degree’, J. Algebra Appl. 15 (2016), 1650132, 8 pages.CrossRefGoogle Scholar
Lusztig, G., ‘On the representations of reductive groups with disconnected centre’, Astérisque 168 (1988), 157–166; Orbites unipotentes et représentations, I.Google Scholar
Malle, G. and Zalesskii, A. E., ‘Prime power degree representations of quasi-simple groups’, Arch. Math. 77 (2001), 461–468.Google Scholar
Michler, G. O., ‘Brauer’s conjectures and the classification of finite simple groups’, in: Representation Theory II, Groups and Orders, Lecture Notes in Mathematics (Springer, Heidelberg, 1986), 129–142.Google Scholar
Navarro, G., ‘The set of character degrees of a finite group does not determine its solvability’, Proc. Amer. Math. Soc. 143 (2015), 989–990.CrossRefGoogle Scholar
Navarro, G. and Tiep, P. H., ‘Characters of relative p-degree over normal subgroups’, Ann. of Math. (2) 178 (2013), 1135–1171.CrossRefGoogle Scholar
Schmidt, P., ‘Rational matrix groups of a special type’, Linear Algebra Appl. 71 (1985), 289–293.CrossRefGoogle Scholar
Schmidt, P., ‘Extending the Steinberg representation’, J. Algebra 150 (1992), 254–256.Google Scholar
White, D. L., ‘Character degrees of extensions of PSL2(q)’, J. Group Theory 16 (2013), 1–33.Google Scholar