Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T17:38:37.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterising complete boolean algebras in terms of pure essentialness

Published online by Cambridge University Press:  17 April 2009

Kiran R. Bhutani
Kiran R. Bhutani
Affiliation:
Department of Mathematics, The Catholic University of America, Washington D.C. 20064, United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We discuss purity and pure essentialness of abelian groups in a topos 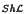of sheaves on a locale 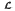and show that purity is not a local property. We prove that 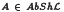is divisible if and only if it is pure in every extension, and give an example of a category in winch absolutely pure does not imply divisible. We discuss uniform abelian groups and show that each AU uniform in Ab does not imply that A is uniform in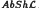

Banaschewski showed that the pure subgroups of 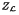are exactly of the type 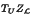for the different 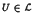. We show that 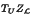is essential in 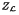if and only if U is dense in 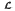, Finally, we characterise as complete boolean algebras the locales for which the only pure and essential subgroup of 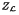is .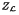

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 38 , Issue 1 , August 1988 , pp. 23 - 30
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Banaschewski, B., ‘When are divisible abelian groups injective?’, Quaestiones Math. 4 (1981), 285–307.CrossRefGoogle Scholar
[2]Banaschewski, B., Recovering a space from its abelian sheaves: Seminar talks (McMaster University, 1980).Google Scholar
[3]Bhutani, K.R., Abelian groups in a topos of sheaves on a locale: Doctoral dissertation (McMaster University, 1983).Google Scholar
[4]Bhutani, K.R., ‘Injectivity and injective hulls of abelian groups in a localic topos’, Bull. Austral. Math. Soc. 37 (1988), 43–59.Google Scholar
[5]Ebrahimi, M., Algebra in a topos of sheaves: Doctoral dissertation (McMaster University, 1980).Google Scholar
[6]Fuchs, L., Infinite Abelian Groups 1 (Academic Press, New York, 1970).Google Scholar
[7]Freyd, P., Abelian Categories (Harper and Row, New York, 1964).Google Scholar
[8]Godement, R., Theorie des Faisceaux (Hermann, Paris, 1958).Google Scholar
[9]Johnstone, P.T., Stone space: Cambridge Stud. Adv. Math. 3 (Cambridge University Press, 1982).Google Scholar
[10]Johnstone, P.T., Topos theory (Academic Press, New York, 1977).Google Scholar
[11]MacLane, S., Categories for the working mathematician: Graduate Texts in Math. 5 (Springer-Verlag, Berlin, 1971).Google Scholar