No CrossRef data available.
Published online by Cambridge University Press: 08 August 2022
We prove that a ring R is an
 $n \times n$
matrix ring (that is,
$n \times n$
matrix ring (that is,
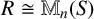 $R \cong \mathbb {M}_n(S)$
for some ring S) if and only if there exists a (von Neumann) regular element x in R such that
$R \cong \mathbb {M}_n(S)$
for some ring S) if and only if there exists a (von Neumann) regular element x in R such that
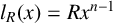 $l_R(x) = R{x^{n-1}}$
. As applications, we prove some new results, strengthen some known results and provide easier proofs of other results. For instance, we prove that if a ring R has elements x and y such that
$l_R(x) = R{x^{n-1}}$
. As applications, we prove some new results, strengthen some known results and provide easier proofs of other results. For instance, we prove that if a ring R has elements x and y such that
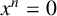 $x^n = 0$
,
$x^n = 0$
,
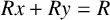 $Rx+Ry = R$
and
$Rx+Ry = R$
and
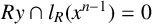 $Ry \cap l_{R}(x^{n-1}) = 0$
, then R is an
$Ry \cap l_{R}(x^{n-1}) = 0$
, then R is an
 $n \times n$
matrix ring. This improves a result of Fuchs [‘A characterisation result for matrix rings’, Bull. Aust. Math. Soc. 43 (1991), 265–267] where it is proved assuming further that the element y is nilpotent of index two and
$n \times n$
matrix ring. This improves a result of Fuchs [‘A characterisation result for matrix rings’, Bull. Aust. Math. Soc. 43 (1991), 265–267] where it is proved assuming further that the element y is nilpotent of index two and
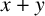 $x+y$
is a unit. For an ideal I of a ring R, we prove that the ring
$x+y$
is a unit. For an ideal I of a ring R, we prove that the ring
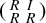 $(\begin {smallmatrix} R & I \\ R & R \end {smallmatrix})$
is a
$(\begin {smallmatrix} R & I \\ R & R \end {smallmatrix})$
is a
 $2 \times 2$
matrix ring if and only if
$2 \times 2$
matrix ring if and only if
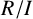 $R/I$
is so.
$R/I$
is so.
The work of the first author is supported by a UGC grant and will form a part of her Ph.D. dissertation under the supervision of the second author.