No CrossRef data available.
Article contents
A characterisation of cyclic subnormal separated A-groups of nilpotent length three
Published online by Cambridge University Press: 17 April 2009
Abstract
The paper gives a detailed description of all those finite A-groups of nilpotent length three that satisfy the cyclic subnormal separation condition. It is shown that every monolithic group under discussion is an extension of its Fitting subgroup P, which is a homocyclic p-group, by a p′ metabelian subgroup H, where p is a prime. The centraliser of P in H is trivial while the monolith W is equal to ω1(P) and the action of H on W is faithful and irreducible. H is further shown to have non trivial centre and is an extension of its derived subgroup M by a subgroup L such that
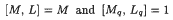
for all primes q where Mq and Lq are the respective Sylow q-subgroups of M and L. The Fitting subgroup of F of H is shown to be M × Z(H), while Z(H) = F ∩ L and every element of L of prime order is in Z(H). Finally it is shown that if ql(q) is the exponent of Mq then every element of order dividing ql(q) in L belongs to Z(H).
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 56 , Issue 2 , October 1997 , pp. 243 - 251
- Copyright
- Copyright © Australian Mathematical Society 1997


