No CrossRef data available.
Article contents
Certain locally nilpotent varieties of groups
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let c ≥ 0, d ≥ 2 be integers and 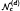 be the variety of groups in which every d-generator subgroup is nilpotent of class at most c. N.D. Gupta asked for what values of c and d is it true that
be the variety of groups in which every d-generator subgroup is nilpotent of class at most c. N.D. Gupta asked for what values of c and d is it true that 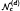 is locally nilpotent? We prove that if c ≤ 2d + 2d−1 − 3 then the variety
is locally nilpotent? We prove that if c ≤ 2d + 2d−1 − 3 then the variety 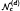 is locally nilpotent and we reduce the question of Gupta about the periodic groups in
is locally nilpotent and we reduce the question of Gupta about the periodic groups in 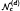 to the prime power exponent groups in this variety.
to the prime power exponent groups in this variety.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 67 , Issue 1 , February 2003 , pp. 115 - 119
- Copyright
- Copyright © Australian Mathematical Society 2003
References
REFERENCES
[1]Endimioni, G., ‘Groups in which every d-generator subgroup is nilpotent of bounded class’, Quart. J. Math. Oxford (2) 46 (1995), 433–435.Google Scholar
[2]Gupta, N.D., ‘Certain locally metanilpotent varieties of groups’, Arch. Math. 20 (1969), 481–484.Google Scholar
[3]Heineken, H., ‘Engelsche Elemente der Länge drei’, Illinois J. Math. 5 (1961), 681–707.Google Scholar
[4]Lubotzky, A. and Mann, A., ‘Powerful p-groups. I. Finite groups’, J. Algebra 105 (1987), 484–505.CrossRefGoogle Scholar
[5]Newell, M.L., ‘On right-Engel elements of length three’, Proc. Roy. Irish Acad. Sect. A 96 (1996), 17–24.Google Scholar
[6]Plotkin, B.I., ‘On the nil-radical of a group’, Dokl. Akad. Nauk SSSR 98 (1954), 341–343.Google Scholar
[7]Robinson, D.J.S., A first course in the group theory, Graduate Texts in Mathematics 80, (Second edition) (Springer-Verlag, New York, 1996).Google Scholar
[8]Shalev, A., ‘Characterization of p-adic analytic groups in terms of wreath products’, J. Algebra 145 (1992), 204–208.Google Scholar
[10]Vaughan-Lee, M., ‘Engel-4 groups of exponent 5’, Proc. London Math. Soc. (3) 74 (1997), 306–334.Google Scholar


