Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T20:53:56.043Z Has data issue: false hasContentIssue false
  • English
  • Français

CATEGORY AND TOPOLOGICAL COMPLEXITY OF THE CONFIGURATION SPACE 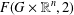$F(G\times \mathbb{R}^{n},2)$

Part of: Fiber spaces and bundles Homotopy theory Classical Topics in Algebraic Topology

Published online by Cambridge University Press:  24 May 2019

CESAR A. IPANAQUE ZAPATA Open the ORCID record for CESAR A. IPANAQUE ZAPATA [Opens in a new window]
CESAR A. IPANAQUE ZAPATA*
Affiliation:
Departamento de Matemática, Universidade de São Paulo, Instituto de Ciências Matemáticas e de Computação - USP, Avenida Trabalhador São-carlense, 400 - Centro CEP: 13566-590, São Carlos - SP, Brasil email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Lusternik–Schnirelmann category cat and topological complexity TC are related homotopy invariants. The topological complexity TC has applications to the robot motion planning problem. We calculate the Lusternik–Schnirelmann category and topological complexity of the ordered configuration space of two distinct points in the product 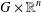$G\times \mathbb{R}^{n}$ and apply the results to the planar and spatial motion of two rigid bodies in 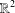$\mathbb{R}^{2}$ and 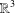$\mathbb{R}^{3}$ respectively.

Keywords

configuration spacescup-lengthzero-divisor cup-lengthtopological complexityLusternik–Schnirelmann category

MSC classification

Primary: 55R80: Discriminantal varieties, configuration spaces
Secondary: 55M30: Ljusternik-Schnirelman (Lyusternik-Shnirel'man) category of a space 55P10: Homotopy equivalences
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 507 - 517
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The author wishes to acknowledge support for this research from grant no. 2016/18714-8, São Paulo Research Foundation (FAPESP).

References

Cohen, D. C., ‘Topological complexity of classical configuration spaces and related objects’, in: Topological Complexity and Related Topics, Contemporary Mathematics, 702 (eds. Grant, M., Lupton, G. and Vandembroucq, L.) (American Mathematical Society, Providence, RI, 2018), 41–60.Google Scholar
Cohen, D. C. and Farber, M., ‘Topological complexity of collision-free motion planning on surfaces’, Compos. Math. 147(2) (2011), 649–660.Google Scholar
Cornea, O., Lupton, G., Oprea, J. and Tanré, D., Lusternik-Schnirelmann Category, Mathematical Surveys and Monographs, 103 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Dranishnikov, A., ‘Topological complexity of wedges and covering maps’, Proc. Amer. Math. Soc. 142(12) (2014), 4365–4376.Google Scholar
Dranishnikov, A. and Sadykov, R., ‘The topological complexity of the free product’. Math. Z., to appear.Google Scholar
Fadell, E. and Neuwirth, L., ‘Configuration spaces’, Math. Scand. 10(4) (1962), 111–118.Google Scholar
Farber, M., ‘Topological complexity of motion planning’, Discrete Comput. Geom. 29(2) (2003), 211–221.Google Scholar
Farber, M., ‘Instabilities of robot motion’, Topol. Appl. 140(2–3) (2004), 245–266.Google Scholar
Farber, M., Invitation to Topological Robotics (European Mathematical Society, Zurich, 2008).Google Scholar
Farber, M., ‘Configuration spaces and robot motion planning algorithms’, in: Combinatorial and Toric Homotopy: Introductory Lectures (eds. Darby, A., Grbić, J. and Wu, J.) (World Scientific, Singapore, 2017), 263–303.Google Scholar
Farber, M. and Grant, M., ‘Topological complexity of configuration spaces’, Proc. Amer. Math. Soc. 137(5) (2009), 1841–1847.Google Scholar
Farber, M., Grant, M. and Yuzvinsky, S., ‘Topological complexity of collision free motion planning algorithms in the presence of multiple moving obstacles’, in: Topology Robotics, Contemporary Mathematics, 438 (eds. Farber, M., Ghrist, R., Burger, M. and Koditschek, D.) (American Mathematical Society, Providence, RI, 2007), 75–84.Google Scholar
Farber, M. and Yuzvinsky, S., ‘Topological robotics: subspace arrangements and collision free motion planning’, in: Geometry, Topology, and Mathematical Physics, American Mathematical Society Translations Series 2, 212 (American Mathematical Society, Providence, RI, 2004), 145–156.Google Scholar
González, J. and Grant, M., ‘Sequential motion planning of noncolliding particles in Euclidean spaces’, Proc. Amer. Math. Soc. 143(10) (2015), 4503–4512.Google Scholar
Iwase, N. and Sakai, M., ‘Topological complexity is a fibrewise L–S category’, Topol. Appl. 157(1) (2010), 10–21.Google Scholar
Iwase, N., Mimura, M. and Nishimoto, T., ‘Lusternik–Schnirelmann category of non-simply connected compact simple Lie groups’, Topol. Appl. 150(1–3) (2005), 111–123.Google Scholar
Iwase, N. and Miyauchi, T., ‘On Lusternik–Schnirelmann category of SO(10)’, Fund. Math. 234(3) (2016), 201–227.Google Scholar
James, I. M., ‘On category, in the sense of Lusternik–Schnirelmann’, Topology 17(4) (1978), 331–348.Google Scholar
Latombe, J.-C., Robot Motion Planning (Springer, New York, 1991).Google Scholar
LaValle, S. M., Planning Algorithms (Cambridge University Press, Cambridge, 2006).Google Scholar
Roth, F., ‘On the category of Euclidean configuration spaces and associated fibrations’, Geom. Topol. Monogr. 13 (2008), 447–461.Google Scholar
Zapata, C. A. I., ‘Collision-free motion planning on manifolds with boundary’, Preprint, 2017, arXiv:1710.00293.Google Scholar
Zapata, C. A. I., ‘Lusternik–Schnirelmann category of the configuration space of complex projective space’, Topol. Proc. 54 (2018), 103–108.Google Scholar
Zapata, C. A. I., ‘Non-contractible configuration spaces’, MORFISMOS 22 (2018), 27–39.Google Scholar