Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T18:02:28.522Z Has data issue: false hasContentIssue false
  • English
  • Français

CARDINALITY OF INVERSE LIMITS WITH UPPER SEMICONTINUOUS BONDING FUNCTIONS

Part of: Fairly general properties Maps and general types of spaces defined by maps Basic constructions

Published online by Cambridge University Press:  23 September 2014

MATEJ ROŠKARIČ  and
NIKO TRATNIK
MATEJ ROŠKARIČ
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška 160, Maribor 2000, Slovenia email [email protected]
NIKO TRATNIK*
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Maribor, Koroška 160, Maribor 2000, Slovenia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We explore the cardinality of generalised inverse limits. Among other things, we show that, for any 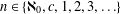$n\in \{ℵ_{0},c,1,2,3,\dots \}$, there is an upper semicontinuous function with the inverse limit having exactly $n$ points. We also prove that if 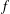$f$ is an upper semicontinuous function whose graph is a continuum, then the cardinality of the corresponding inverse limit is either 1, 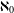$ℵ_{0}$ or $c$. This generalises the recent result of I. Banič and J. Kennedy, which claims that the same is true in the case where the graph is an arc.

Keywords

continualimitsinverse limitscardinalityupper semicontinuous set-valued functions

MSC classification

Primary: 54C60: Set-valued maps
Secondary: 54B10: Product spaces 54D80: Special constructions of spaces (spaces of ultrafilters, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 167 - 174
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Banič, I., Črepnjak, M., Merhar, M. and Milutinović, U., ‘Towards the complete classification of tent maps inverse limits’, Topology Appl. 160 (2013), 63–73.Google Scholar
Banič, I. and Kennedy, J., ‘Inverse limits with bonding functions whose graphs are arcs’, Preprint.Google Scholar
Ingram, W. T., An Introduction to Inverse Limits with Set-Valued Functions (Springer, New York, 2012).Google Scholar
Ingram, W. T. and Mahavier, W. S., ‘Inverse limits of upper semi-continuous set valued functions’, Houston J. Math. 32 (2006), 119–130.Google Scholar
Mahavier, W. S., ‘Inverse limits with subsets of [0, 1] × [0, 1]’, Topology Appl. 141 (2004), 225–231.Google Scholar
Nadler, S. B., Continuum Theory: An Introduction, Monographs and Textbooks in Pure and Applied Mathematics 158 (Marcel Dekker, New York, 1992).Google Scholar