Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T16:34:36.209Z Has data issue: false hasContentIssue false
  • English
  • Français

A BIJECTION OF INVARIANT MEANS ON AN AMENABLE GROUP WITH THOSE ON A LATTICE SUBGROUP

Part of: Noncompact transformation groups Abstract harmonic analysis

Published online by Cambridge University Press:  18 January 2021

JOHN HOPFENSPERGER Open the ORCID record for JOHN HOPFENSPERGER [Opens in a new window]
JOHN HOPFENSPERGER*
Affiliation:
Department of Mathematics, University at Buffalo, Buffalo, NY14260-2900, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

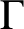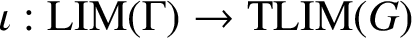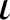Suppose G is an amenable locally compact group with lattice subgroup $\Gamma $ . Grosvenor [‘A relation between invariant means on Lie groups and invariant means on their discrete subgroups’, Trans. Amer. Math. Soc.288(2) (1985), 813–825] showed that there is a natural affine injection $\iota : {\text {LIM}}(\Gamma )\to {\text {TLIM}}(G)$ and that $\iota $ is a surjection essentially in the case 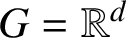$G={\mathbb R}^d$ , 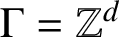$\Gamma ={\mathbb Z}^d$ . In the present paper it is shown that 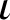$\iota $ is a surjection if and only if 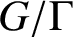$G/\Gamma $ is compact.

Keywords

amenable groupsFølner netsinvariant meanslattices

MSC classification

Primary: 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 22F30: Homogeneous spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 302 - 307
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bader, U., Caprace, P.-E., Gelander, T. and Mozes, S., ‘Lattices in amenable groups’, Fundamenta Math. 246(3) (2019), 217–255.CrossRefGoogle Scholar
Greenleaf, F. P., Invariant Means on Topological Groups and Their Applications (Van Nostrand, New York, 1969).Google Scholar
Grosvenor, J. R., ‘A relation between invariant means on Lie groups and invariant means on their discrete subgroups’, Trans. Amer. Math. Soc. 288(2) (1985), 813–825.CrossRefGoogle Scholar
Hopfensperger, J., ‘When is an invariant mean the limit of a Følner net?’, Preprint, 2020, arXiv:2003.00251 [math.FA].CrossRefGoogle Scholar
Paterson, A. L. T., Amenability (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Raughunathan, M. S., Discrete Subgroups of Lie Groups (Springer-Verlag, Berlin, 1972).CrossRefGoogle Scholar
Weil, A., L’Intégration dans les Groupes Topologiques et ses Applications (Hermann, Paris, 1953).Google Scholar