Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T20:06:58.887Z Has data issue: false hasContentIssue false
  • English
  • Français

AVERAGES OF EXPONENTIAL TWISTS OF THE VON MANGOLDT FUNCTION

Part of: Zeta and $L$-functions: analytic theory Exponential sums and character sums

Published online by Cambridge University Press:  25 April 2022

XIUMIN REN  and
WEI ZHANG Open the ORCID record for WEI ZHANG [Opens in a new window]
XIUMIN REN
Affiliation:
School of Mathematics, Shandong University, Jinan, Shandong 250100, PR China e-mail: [email protected]
WEI ZHANG*
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng, Henan 475004, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain some improved results for the exponential sum 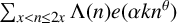$\sum _{x<n\leq 2x}\Lambda (n)e(\alpha k n^{\theta })$ with 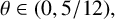$\theta \in (0,5/12),$ where 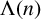$\Lambda (n)$ is the von Mangoldt function. Such exponential sums have relations with the so-called quasi-Riemann hypothesis and were considered by Murty and Srinivas [‘On the uniform distribution of certain sequences’, Ramanujan J. 7 (2003), 185–192].

Keywords

exponential sums over primeszero-density estimates

MSC classification

Primary: 11L20: Sums over primes
Secondary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 425 - 430
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by National Natural Science Foundation of China (Grant No. 11871307).

References

Huxley, M. N., ‘On the difference between consecutive primes’, Invent. Math. 15 (1972), 164–170.CrossRefGoogle Scholar
Ingham, A. E., ‘On the estimation of $N\left(\sigma, T\right)$ ’, Q. J. Math. 15 (1940), 291–292.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H., Luo, W. Z. and Sarnak, P., ‘Low lying zeros of families of $L$ -functions’, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.CrossRefGoogle Scholar
Murty, M. R. and Srinivas, K., ‘On the uniform distribution of certain sequences’, Ramanujan J. 7 (2003), 185–192.CrossRefGoogle Scholar
Ren, X. M., ‘Vinogradov’s exponential sum over primes’, Acta Arith. 124 (2006), 269–285.CrossRefGoogle Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (Oxford University Press, Oxford, 1986).Google Scholar
Vinogradov, I. M., Special Variants of the Method of Trigonometric Sums (Nauka, Moscow, 1976) (in Russian); English translation I. M. Vinogradov, Selected Works (Springer, Berlin, 1985).Google Scholar