Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-15T18:21:09.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Average distances in compact connected spaces

Published online by Cambridge University Press:  17 April 2009

David Yost
David Yost
Affiliation:
Department of Pure Mathematics, La Trobe University, Bundoora, Victoria 3083, Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a simple proof of the fact that compact, connected topological spaces have the “average distance property”. For a metric space (X, d), this asserts the existence of a unique number a = a(X) such that, given finitely many points x1, …, xn ∈ X, then there is some y ∈ X with

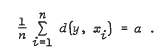
We examine the possible values of a(X) , for subsets of finite dimensional normed spaces. For example, if diam(X) denotes the diameter of some compact, convex set in a euclidean space, then a(X) ≤ diam(X)/√2 . On the other hand, a(X)/diam(X) can be arbitrarily close to 1 , for non-convex sets in euclidean spaces of sufficiently large dimension.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 26 , Issue 3 , December 1982 , pp. 331 - 342
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Gross, O., “The rendezvous value of a metric space”, Advances in game theory, 49–53 (Annals of Mathematics Studies, 52. Princeton University Press, Princeton, New Jersey, 1964).Google Scholar
[2]Hausdorff, Felix, Set theory, 2nd edition (Chelsea, New York, 1962).Google Scholar
[3]Helly, Ed., “Über Mengen knovexer Körper mit gemeinschaftlichen Punkten”, Deutsche Math.-Ver. 32 (1923), 175–176.Google Scholar
[4]Holmes, Richard B., Geometric functional analysis and its applications (Graduate Texts in Mathematics, 24. Springer-Verlag, New York, Heidelberg, Berlin, 1975).CrossRefGoogle Scholar
[5]Morris, Sidney A. and Nickolas, Peter, “On the average distance property of compact connected metric spaces”, Arch. Math. (to appear).Google Scholar
[6]Nikaidô, Hukukane, “On von Neumann's minimax theorem”, Pacific J. Math. 4 (1954), 65–72.CrossRefGoogle Scholar
[7]Stadje, Wolfgang, “A property of compact connected spaces”, Arch. Math. (Basel) 36 (1981), 275–280.CrossRefGoogle Scholar
[8]Strantzen, John, “An average distance result in Euclidean n-space”, Bull. Austral. Math. Soc. 26 (1982), 321–330.CrossRefGoogle Scholar
[9]Szekeres, E. and Szekeres, G., “The average distance theorem for compact convex regions”, Bull. Austral. Math. Soc. (to appear).Google Scholar
[10]Wilson, D.J., “A game with squared distance as payoff”, Bull. Austral, Math. Soc. (to appear).Google Scholar