Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:54:22.681Z Has data issue: false hasContentIssue false
  • English
  • Français

AUTOMORPHISM GROUPS OF SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS

Part of: Graph theory Permutation groups

Published online by Cambridge University Press:  11 November 2015

ZHAOHONG HUANG ,
JIANGMIN PAN ,
SUYUN DING  and
ZHE LIU
ZHAOHONG HUANG
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunming, PR China
JIANGMIN PAN*
Affiliation:
School of Statistics and Mathematics, Yunnan University of Finance and Economics, Kunming, PR China email [email protected]
SUYUN DING
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunming, PR China
ZHE LIU
Affiliation:
College of Science, Zhejiang University of Agriculture and Forestry, Hangzhou, PR China
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Li et al. [‘On finite self-complementary metacirculants’, J. Algebraic Combin.40 (2014), 1135–1144] proved that the automorphism group of a self-complementary metacirculant is either soluble or has 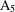$\text{A}_{5}$ as the only insoluble composition factor, and gave a construction of such graphs with insoluble automorphism groups (which are the first examples of self-complementary graphs with this property). In this paper, we will prove that each simple group is a subgroup (so is a section) of the automorphism groups of infinitely many self-complementary vertex-transitive graphs. The proof involves a construction of such graphs. We will also determine all simple sections of the automorphism groups of self-complementary vertex-transitive graphs of 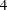$4$-power-free order.

Keywords

self-complementary graphautomorphism groupsimple section

MSC classification

Primary: 20B15: Primitive groups
Secondary: 20B30: Symmetric groups 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 238 - 247
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Alspach, B., Morris, J. and Vilfred, V., ‘Self-complementay circulant graphs’, Ars Combin. 53 (1999), 187–191.Google Scholar
Beezer, R. A., ‘Sylow subgraphs in self-complementary vertex transitive graphs’, Expo. Math. 24(2) (2006), 185–194.CrossRefGoogle Scholar
Biggs, N., Algebraic Graph Theory, 2nd edn (Cambridge University Press, New York, 1992).Google Scholar
Chvátal, V., Erdös, P. and Hedrlín, Z., ‘Ramsey’s theorem and self-complementary graphs’, Discrete Math. 3 (1972), 301–304.Google Scholar
Clapham, C. R. J., ‘A class of self-complementary graphs and lower bounds of some Ramsey numbers’, J. Graph Theory 3(3) (1979), 287–289.CrossRefGoogle Scholar
Dobson, E., ‘On self-complementary vertex-transitive graphs of order a product of distinct primes’, Ars Combin. 71 (2004), 249–256.Google Scholar
Figueroa, D. and Giudici, R. E., ‘Group generation of self-complementary graphs’, in: Combinatorics and Graph Theory (Hefei, 1992) (World Scientific, River Edge, NJ, 1993), 131–140.Google Scholar
Flannery, D. L. and O’Brien, E. A., ‘Linear groups of small degree over finite fields’, Internat. J. Algebra Comput. 15 (2005), 467–502.Google Scholar
Godsil, C. D., ‘On the full automorphism group of a graph’, Combinatorica 1 (1981), 243–256.CrossRefGoogle Scholar
Guldan, F. and Tomasta, P., ‘New lower bounds of some diagonal Ramsey numbers’, J. Graph Theory 7(1) (1983), 149–151.Google Scholar
Guralnick, R. M., Li, C. H., Praeger, C. E. and Saxl, J., ‘On orbital partitions and exceptionality of primitive permutation groups’, Trans. Amer. Math. Soc. 356(12) (2004), 4857–4872.CrossRefGoogle Scholar
Li, C. H. and Praeger, C. E., ‘On partitioning the orbitals of a transitive permutation group’, Trans. Amer. Math. Soc. 355(2) (2003), 637–653.CrossRefGoogle Scholar
Li, C. H. and Qiao, S. H., ‘Finite groups of fourth-free order’, J. Group Theory 16(2) (2013), 275–298.Google Scholar
Li, C. H. and Rao, G., ‘Self-complementary vertex-transitive graphs of order a product of two primes’, Bull. Aust. Math. Soc. 89 (2014), 322–330.Google Scholar
Li, C. H., Rao, G. and Song, S. J., ‘On finite self-complementary metacirculants’, J. Algebraic Combin. 40 (2014), 1135–1144.Google Scholar
Mathon, R., ‘On self-complementary strongly regular graphs’, Discrete Math. 69 (1988), 263–281.Google Scholar
Muzychuk, M., ‘On Sylow subgraphs of vertex-transitive self-complementary graphs’, Bull. Lond. Math. Soc. 31(5) (1999), 531–533.CrossRefGoogle Scholar
Robinson, D. J. S., A Course in the Theory of Groups (Springer, New York, 1982).Google Scholar
Rödl, V. and Šiňajová, E., ‘Note on Ramsey numbers and self-complementary graphs’, Math. Slovaca 45(3) (1995), 243–249.Google Scholar
Suprunenko, D. A., ‘Selfcomplementary graphs’, Cybernetics 21 (1985), 559–567.CrossRefGoogle Scholar
Zelinka, B., ‘Self-complementary vertex-transitive undirected graphs’, Math. Slovaca 29 (1979), 91–95.Google Scholar