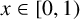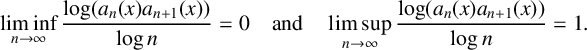1. Introduction
Every
![]() $x\in \mathbb {I}:=[0,1)\backslash \mathbb {Q}$
admits a unique continued fraction expansion of the form
$x\in \mathbb {I}:=[0,1)\backslash \mathbb {Q}$
admits a unique continued fraction expansion of the form
 $$ \begin{align*} x = \dfrac{1}{a_1(x) +\dfrac{1}{a_2(x) + \dfrac{1}{a_3(x)+ \dfrac{1}{\ddots}}}}=:[a_1(x),a_2(x),a_3(x),\ldots], \end{align*} $$
$$ \begin{align*} x = \dfrac{1}{a_1(x) +\dfrac{1}{a_2(x) + \dfrac{1}{a_3(x)+ \dfrac{1}{\ddots}}}}=:[a_1(x),a_2(x),a_3(x),\ldots], \end{align*} $$
where
![]() $a_1(x),a_2(x),a_3(x),\ldots $
are positive integers, called the partial quotients of x. Set
$a_1(x),a_2(x),a_3(x),\ldots $
are positive integers, called the partial quotients of x. Set
![]() $p_n(x)/q_n(x):=[a_1(x),a_2(x),\ldots , a_n(x)]$
, the nth convergent of x.
$p_n(x)/q_n(x):=[a_1(x),a_2(x),\ldots , a_n(x)]$
, the nth convergent of x.
Continued fractions are closely connected with the theory of Diophantine approximation (see [Reference Cassels7, Reference Schmidt22]). For example, Dirichlet’s theorem (see [Reference Schmidt22, Theorem I.1A]) states that, for any
![]() $x\in [0,1)$
and
$x\in [0,1)$
and
![]() $Q>1$
, there exist integers
$Q>1$
, there exist integers
![]() $p,q$
such that
$p,q$
such that
![]() $1\leq q<Q$
and
$1\leq q<Q$
and
A natural question to ask is what happens if the right-hand side of (1.1) is replaced by a faster decreasing function of Q. More precisely, for a nonincreasing function
![]() $\psi : \mathbb {N} \to \mathbb {R}_+$
, let
$\psi : \mathbb {N} \to \mathbb {R}_+$
, let
![]() $D(\psi )$
be the set of
$D(\psi )$
be the set of
![]() $x\in [0,1)$
for which the system
$x\in [0,1)$
for which the system
![]() $1\leq q<Q$
and
$1\leq q<Q$
and
![]() $|qx-p|< \psi (Q)$
has a nontrivial integer solution for all sufficiently large Q. Recently, under the assumption that
$|qx-p|< \psi (Q)$
has a nontrivial integer solution for all sufficiently large Q. Recently, under the assumption that
![]() $q\psi (q) <1$
for all large q, Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] characterised the elements of the complement of
$q\psi (q) <1$
for all large q, Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] characterised the elements of the complement of
![]() $D(\psi )$
, denoted by
$D(\psi )$
, denoted by
![]() $D^{c}(\psi )$
, in terms of continued fractions: that is,
$D^{c}(\psi )$
, in terms of continued fractions: that is,
 $$ \begin{align*} \{x\in \mathbb{I} & \,: a_{n}(x)a_{n+1}(x)\geq \Phi(q_n(x)) \text{ for infinitely many } n \in \mathbb{N}\}\subseteq D^{c}(\psi)\\ &\subseteq \{x\in\mathbb{I}: a_{n}(x)a_{n+1}(x)\geq 4^{-1}\Phi(q_n(x)) \text{ for infinitely many } n \in \mathbb{N}\}, \end{align*} $$
$$ \begin{align*} \{x\in \mathbb{I} & \,: a_{n}(x)a_{n+1}(x)\geq \Phi(q_n(x)) \text{ for infinitely many } n \in \mathbb{N}\}\subseteq D^{c}(\psi)\\ &\subseteq \{x\in\mathbb{I}: a_{n}(x)a_{n+1}(x)\geq 4^{-1}\Phi(q_n(x)) \text{ for infinitely many } n \in \mathbb{N}\}, \end{align*} $$
where
 $$ \begin{align*} \Phi(q) := \frac{q\psi(q)}{1-q\psi(q)}. \end{align*} $$
$$ \begin{align*} \Phi(q) := \frac{q\psi(q)}{1-q\psi(q)}. \end{align*} $$
This leads to the relative growth rate of the product of two consecutive partial quotients
![]() $\{a_n(x)a_{n+1}(x)\}_{n \geq 1}$
compared with
$\{a_n(x)a_{n+1}(x)\}_{n \geq 1}$
compared with
![]() $\{q_n(x)\}_{n\geq 1}$
. Much attention has been paid to the set of points
$\{q_n(x)\}_{n\geq 1}$
. Much attention has been paid to the set of points
![]() $x\in \mathbb {I}$
such that
$x\in \mathbb {I}$
such that
![]() $a_{n}(x)a_{n+1}(x)\geq \Phi (q_n(x))$
for infinitely many
$a_{n}(x)a_{n+1}(x)\geq \Phi (q_n(x))$
for infinitely many
![]() $n \in \mathbb {N}$
. For example, Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] obtained a zero-one law for the Lebesgue measure of this set. Hussain et al. [Reference Hussain, Kleinbock, Wadleigh and Wang14] and Bos et al. [Reference Bos, Hussain and Simmons5] studied its Hausdorff measure. As a consequence of their results, we see that the set of
$n \in \mathbb {N}$
. For example, Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] obtained a zero-one law for the Lebesgue measure of this set. Hussain et al. [Reference Hussain, Kleinbock, Wadleigh and Wang14] and Bos et al. [Reference Bos, Hussain and Simmons5] studied its Hausdorff measure. As a consequence of their results, we see that the set of
![]() $x\in \mathbb I$
for which
$x\in \mathbb I$
for which
 $$ \begin{align} \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log q_n(x)} =\tau \end{align} $$
$$ \begin{align} \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log q_n(x)} =\tau \end{align} $$
has Hausdorff dimension
![]() ${2}/{(2+\tau )}$
for any
${2}/{(2+\tau )}$
for any
![]() $\tau \geq 0$
. Huang and Wu [Reference Huang and Wu12] calculated the Hausdorff dimension of the analogous set where the limsup in (1.2) is replaced by a limit. Feng and Xu [Reference Feng and Xu11] determined the Hausdorff dimension of the subtle set in which the limsup and liminf behaviours of the sequence in (1.2) are considered together. For more results on the relative growth rate of the product of consecutive partial quotients, we refer the reader to [Reference Bakhtawar1, Reference Bakhtawar, Bos and Hussain3, Reference Li, Wang and Xu18] and the references therein.
$\tau \geq 0$
. Huang and Wu [Reference Huang and Wu12] calculated the Hausdorff dimension of the analogous set where the limsup in (1.2) is replaced by a limit. Feng and Xu [Reference Feng and Xu11] determined the Hausdorff dimension of the subtle set in which the limsup and liminf behaviours of the sequence in (1.2) are considered together. For more results on the relative growth rate of the product of consecutive partial quotients, we refer the reader to [Reference Bakhtawar1, Reference Bakhtawar, Bos and Hussain3, Reference Li, Wang and Xu18] and the references therein.
In this paper, we are concerned with the asymptotic behaviour of the product of consecutive partial quotients itself. In this direction, there are many results related to the limsup behaviour (see [Reference Bakhtawar, Bos and Hussain2, Reference Fang, Ma, Song and Yang10, Reference Huang, Wu and Xu13, Reference Hussain, Li and Shulga15]). However, few results address the liminf behaviour. We provide the exact liminf and limsup behaviours of
![]() $\log (a_n(x)a_{n+1}(x))$
. Combining Theorem 3.6 of [Reference Kleinbock and Wadleigh17] and some basic facts of continued fractions gives the following theorem.
$\log (a_n(x)a_{n+1}(x))$
. Combining Theorem 3.6 of [Reference Kleinbock and Wadleigh17] and some basic facts of continued fractions gives the following theorem.
Theorem 1.1. For Lebesgue almost all
![]() $x\in \mathbb {I}$
,
$x\in \mathbb {I}$
,
 $$ \begin{align} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0 \quad \text{and} \quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align} $$
$$ \begin{align} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0 \quad \text{and} \quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align} $$
Theorem 1.1 shows that, for almost all
![]() $x\in \mathbb {I}$
, the liminf and the limsup in (1.3) have different values. In other words, the set of points for which the liminf and the limsup are the same or have other different values is of Lebesgue measure zero. So it is natural to ask how large or small the sizes of such null sets are.
$x\in \mathbb {I}$
, the liminf and the limsup in (1.3) have different values. In other words, the set of points for which the liminf and the limsup are the same or have other different values is of Lebesgue measure zero. So it is natural to ask how large or small the sizes of such null sets are.
For any
![]() $\alpha ,\beta \in [0,\infty ]$
with
$\alpha ,\beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
, let
$\alpha \leq \beta $
, let
 $$ \begin{align*} E(\alpha,\beta):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\alpha,\ \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}=\beta\bigg\}. \end{align*} $$
$$ \begin{align*} E(\alpha,\beta):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\alpha,\ \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}=\beta\bigg\}. \end{align*} $$
Baire category and Hausdorff dimension are two common ways beyond the Lebesgue measure to determine large and small sets, and they have been widely used to study the ‘size’ of various sets in continued fractions (see [Reference Chang, Dong, Liu and Shang8, Reference Olsen20, Reference Shang and Wu23]). We investigate the Baire category and the Hausdorff dimension of
![]() $E(\alpha ,\beta )$
. Recall that a set is said to be of first category if it can be represented as a countable union of nowhere dense sets, and a set is residual if its complement is of first category. In a certain sense, a set of first category is considered small, whereas a residual set is large. We will see that
$E(\alpha ,\beta )$
. Recall that a set is said to be of first category if it can be represented as a countable union of nowhere dense sets, and a set is residual if its complement is of first category. In a certain sense, a set of first category is considered small, whereas a residual set is large. We will see that
![]() $E(\alpha ,\beta )$
is residual for the extreme case where
$E(\alpha ,\beta )$
is residual for the extreme case where
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\beta =\infty $
; otherwise it is of first category.
$\beta =\infty $
; otherwise it is of first category.
Theorem 1.2. The set
![]() $E(\alpha ,\beta )$
is residual if and only if
$E(\alpha ,\beta )$
is residual if and only if
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\beta =\infty $
.
$\beta =\infty $
.
Theorems 1.1 and 1.2 imply that
![]() $E(0,1)$
is large in the sense of Lebesgue measure, whereas it is small from a Baire category point of view. On the contrary,
$E(0,1)$
is large in the sense of Lebesgue measure, whereas it is small from a Baire category point of view. On the contrary,
![]() $E(0,\infty )$
is small in the sense of Lebesgue measure, but large from a Baire category point of view. Moreover, the set of points for which the liminf and the limsup in (1.3) share the same values is small in both senses. The following theorem shows that
$E(0,\infty )$
is small in the sense of Lebesgue measure, but large from a Baire category point of view. Moreover, the set of points for which the liminf and the limsup in (1.3) share the same values is small in both senses. The following theorem shows that
![]() $E(\alpha ,\beta )$
is not that small for all
$E(\alpha ,\beta )$
is not that small for all
![]() $\alpha ,\beta \in [0,\infty ]$
with
$\alpha ,\beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
in the sense of Hausdorff dimension.
$\alpha \leq \beta $
in the sense of Hausdorff dimension.
Theorem 1.3. For
![]() $\alpha , \beta \in [0,\infty ]$
with
$\alpha , \beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
,
$\alpha \leq \beta $
,
 $$ \begin{align*} \dim_{\mathrm{H}} E(\alpha,\beta) = \left\{\!\! \begin{array}{ll} 1 & \text{for } \alpha=0, \\ \frac{1}{2} &\text{for } \alpha>0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}} E(\alpha,\beta) = \left\{\!\! \begin{array}{ll} 1 & \text{for } \alpha=0, \\ \frac{1}{2} &\text{for } \alpha>0. \end{array} \right. \end{align*} $$
The rest of the paper is organised as follows. In Section 2, we give the proof of Theorem 1.1, the ingredients of which include the Fatou lemma in analysis and a zero-one law for the product of consecutive partial quotients in [Reference Kleinbock and Wadleigh17]. Section 3 is devoted to the proof of Theorem 1.2. We remark that the method in this section can be applied to study the Baire category of the sets considered in [Reference Feng and Xu11, Reference Huang and Wu12] (see Remark 3.3). In Section 4, we give the proof of the Hausdorff dimension of
![]() $E(\alpha ,\beta )$
. Finally, we do some similar analysis for the weighted product of consecutive partial quotients.
$E(\alpha ,\beta )$
. Finally, we do some similar analysis for the weighted product of consecutive partial quotients.
2. Proof of Theorem 1.1
To prove Theorem 1.1, it suffices to show that the values given for the liminf and limsup hold for Lebesgue almost all
![]() $x\in \mathbb {I}$
. We first consider the liminf.
$x\in \mathbb {I}$
. We first consider the liminf.
Lemma 2.1. For any
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
Then
![]() $\mathcal {L}(A_k) =1$
, where
$\mathcal {L}(A_k) =1$
, where
![]() $\mathcal {L}$
denotes the Lebesgue measure.
$\mathcal {L}$
denotes the Lebesgue measure.
Proof. Fix
![]() $k \in \mathbb {N}$
. We denote by
$k \in \mathbb {N}$
. We denote by
![]() $B_k$
the complement of
$B_k$
the complement of
![]() $A_k$
, namely,
$A_k$
, namely,
 $$ \begin{align*} B_k = \{ x \in \mathbb{I}:a_n(x)a_{n+1}(x)\ge n^{1/k} \text{ for sufficiently large } n\in{\mathbb N}\} = \bigcup^{\infty}_{N=1}\bigcap^{\infty}_{n=N} B_{k,n}, \end{align*} $$
$$ \begin{align*} B_k = \{ x \in \mathbb{I}:a_n(x)a_{n+1}(x)\ge n^{1/k} \text{ for sufficiently large } n\in{\mathbb N}\} = \bigcup^{\infty}_{N=1}\bigcap^{\infty}_{n=N} B_{k,n}, \end{align*} $$
where
![]() $B_{k,n}:=\{ x \in \mathbb {I}:a_n(x)a_{n+1}(x)\ge n^{1/k}\}$
. Then
$B_{k,n}:=\{ x \in \mathbb {I}:a_n(x)a_{n+1}(x)\ge n^{1/k}\}$
. Then
![]() $\mathcal {L}(A_k)=1-\mathcal {L}(B_k)$
. It follows from the Fatou lemma that
$\mathcal {L}(A_k)=1-\mathcal {L}(B_k)$
. It follows from the Fatou lemma that
which leads to an estimate for the Lebesgue measure of
![]() $B_{k,n}$
. Note that
$B_{k,n}$
. Note that
![]() $B_{k,n}$
is a subset of the set
$B_{k,n}$
is a subset of the set
Combining this with (2.1) and the fact that, for any
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
we deduce that
 $$ \begin{align*} \mathcal{L}(A_k) &\geq 1-\liminf_{n \to \infty}\mathcal{L}(B_{k,n}) \\ &\geq 1- \liminf_{n \to \infty} (\mathcal{L}\{ x \in \mathbb{I}:a_n(x)\ge n^{1/{(2k)}}\} + \mathcal{L}\{ x \in \mathbb{I}:a_{n+1}(x)\ge n^{1/{(2k)}}\})\\ &\geq 1- \liminf_{n \to \infty} \frac{4}{n^{1/(2k)}}=1. \end{align*} $$
$$ \begin{align*} \mathcal{L}(A_k) &\geq 1-\liminf_{n \to \infty}\mathcal{L}(B_{k,n}) \\ &\geq 1- \liminf_{n \to \infty} (\mathcal{L}\{ x \in \mathbb{I}:a_n(x)\ge n^{1/{(2k)}}\} + \mathcal{L}\{ x \in \mathbb{I}:a_{n+1}(x)\ge n^{1/{(2k)}}\})\\ &\geq 1- \liminf_{n \to \infty} \frac{4}{n^{1/(2k)}}=1. \end{align*} $$
So
![]() $\mathcal {L}(A_k) =1$
.
$\mathcal {L}(A_k) =1$
.
Let
![]() $A=\bigcap ^\infty _{k=1}A_k$
. Then
$A=\bigcap ^\infty _{k=1}A_k$
. Then
![]() $\mathcal {L}(A) =1$
. For
$\mathcal {L}(A) =1$
. For
![]() $x\in A$
, we see that, for any k,
$x\in A$
, we see that, for any k,
![]() $a_n(x)a_{n+1}(x) <n^{1/k}$
for infinitely many n, which implies that
$a_n(x)a_{n+1}(x) <n^{1/k}$
for infinitely many n, which implies that
 $$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq \frac{1}{k}. \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq \frac{1}{k}. \end{align*} $$
Letting
![]() $k \to \infty $
shows that the liminf is equal to zero.
$k \to \infty $
shows that the liminf is equal to zero.
For the limsup, we need the following lemma established by Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17]; see Huang et al. [Reference Huang, Wu and Xu13] for a general result.
Lemma 2.2 [Reference Kleinbock and Wadleigh17, Theorem 3.6].
Let
![]() $\psi : \mathbb {N} \to (1,\infty )$
be a positive function with
$\psi : \mathbb {N} \to (1,\infty )$
be a positive function with
![]() ${\psi (n) \to \infty} $
as
${\psi (n) \to \infty} $
as
![]() $n \to \infty $
. Write
$n \to \infty $
. Write
Then
 $$ \begin{align*} \mathcal{L}(E_\psi) = \begin{cases} 0 & \displaystyle\text{if } \sum^\infty_{n=1}{\log\psi(n)}/{\psi(n)} <\infty, \\ 1 & \displaystyle\text{if } \sum^\infty_{n=1}{\log\psi(n)}/{\psi(n)} =\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{L}(E_\psi) = \begin{cases} 0 & \displaystyle\text{if } \sum^\infty_{n=1}{\log\psi(n)}/{\psi(n)} <\infty, \\ 1 & \displaystyle\text{if } \sum^\infty_{n=1}{\log\psi(n)}/{\psi(n)} =\infty. \end{cases} \end{align*} $$
For any
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
and
Taking
![]() $\psi (n) = n^{1+1/k}$
and
$\psi (n) = n^{1+1/k}$
and
![]() $\psi (n) = n^{1-1/k}$
in Lemma 2.2, we deduce that the complement of
$\psi (n) = n^{1-1/k}$
in Lemma 2.2, we deduce that the complement of
![]() $C_k$
has null Lebesgue measure (that is,
$C_k$
has null Lebesgue measure (that is,
![]() $\mathcal {L}(C_k)=1$
) and
$\mathcal {L}(C_k)=1$
) and
![]() $D_k$
is of Lebesgue measure one. Let
$D_k$
is of Lebesgue measure one. Let
![]() $B= \bigcap ^\infty _{k=1} (C_k \cap D_k)$
. Then
$B= \bigcap ^\infty _{k=1} (C_k \cap D_k)$
. Then
![]() $\mathcal {L}(B)=1$
. For
$\mathcal {L}(B)=1$
. For
![]() $x\in B$
, we see that, for any large k,
$x\in B$
, we see that, for any large k,
 $$ \begin{align*} 1-\frac{1}{k} \leq \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq 1+\frac{1}{k}. \end{align*} $$
$$ \begin{align*} 1-\frac{1}{k} \leq \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq 1+\frac{1}{k}. \end{align*} $$
Letting
![]() $k \to \infty $
shows that the limsup equals one.
$k \to \infty $
shows that the limsup equals one.
For the proof of Theorem 1.1, let
![]() $C=A\cap B$
. Then
$C=A\cap B$
. Then
![]() $\mathcal {L}(C)=1$
. Moreover, for any
$\mathcal {L}(C)=1$
. Moreover, for any
![]() $x\in C$
,
$x\in C$
,
 $$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0\quad\text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = 0\quad\text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=1. \end{align*} $$
3. Proof of Theorem 1.2
In this section, the underlying topological space is
![]() $\mathbb {I}$
with the induced topology. Since
$\mathbb {I}$
with the induced topology. Since
![]() $\mathbb {I}$
is a Baire space, to prove that a set is residual, it is sufficient to show that it contains a dense
$\mathbb {I}$
is a Baire space, to prove that a set is residual, it is sufficient to show that it contains a dense
![]() $G_\delta $
subset (see [Reference Oxtoby21, Theorem 9.2]). To this end, for
$G_\delta $
subset (see [Reference Oxtoby21, Theorem 9.2]). To this end, for
![]() $\gamma \in (0,\infty )$
, let
$\gamma \in (0,\infty )$
, let
 $$ \begin{align*} E(\gamma):=\bigg\{x\in \mathbb{I}: \lim_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\gamma\bigg\}. \end{align*} $$
$$ \begin{align*} E(\gamma):=\bigg\{x\in \mathbb{I}: \lim_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\gamma\bigg\}. \end{align*} $$
Lemma 3.1. For any
![]() $\gamma \in (0,\infty )$
,
$\gamma \in (0,\infty )$
,
![]() $E(\gamma )$
is dense in
$E(\gamma )$
is dense in
![]() $\mathbb {I}$
.
$\mathbb {I}$
.
Proof. For
![]() $\gamma \in (0,\infty )$
, let
$\gamma \in (0,\infty )$
, let
![]() $\sigma _n:=\lceil n^{1/\gamma }\rceil $
for all n. Then the sequence
$\sigma _n:=\lceil n^{1/\gamma }\rceil $
for all n. Then the sequence
![]() $\{\sigma _n\}$
corresponds to a unique irrational number
$\{\sigma _n\}$
corresponds to a unique irrational number
![]() $x_0 \in [0,1]$
such that
$x_0 \in [0,1]$
such that
![]() $a_n(x_0) =\sigma _n$
for all
$a_n(x_0) =\sigma _n$
for all
![]() $n \geq 1$
. Hence,
$n \geq 1$
. Hence,
 $$ \begin{align*} \lim_{n \to \infty} \frac{\log (a_n(x_0)a_{n+1}(x_0))}{\log n}=\gamma, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{\log (a_n(x_0)a_{n+1}(x_0))}{\log n}=\gamma, \end{align*} $$
that is,
![]() $x_0 \in E(\gamma )$
. Put
$x_0 \in E(\gamma )$
. Put
 $$ \begin{align*} \mathcal{D}(x_0):=\bigcup_{N=1}^{\infty}\{x\in \mathbb{I}: a_n(x)=a_n(x_0) \ \text{for all } n\geq N\}. \end{align*} $$
$$ \begin{align*} \mathcal{D}(x_0):=\bigcup_{N=1}^{\infty}\{x\in \mathbb{I}: a_n(x)=a_n(x_0) \ \text{for all } n\geq N\}. \end{align*} $$
Then
![]() $\mathcal {D}(x_0) \subseteq E(\gamma )$
is dense in
$\mathcal {D}(x_0) \subseteq E(\gamma )$
is dense in
![]() $\mathbb {I}$
. To see this, for any
$\mathbb {I}$
. To see this, for any
![]() $x\in \mathbb {I}$
, define
$x\in \mathbb {I}$
, define
![]() $x_n$
in terms of the continued fraction expansion as
$x_n$
in terms of the continued fraction expansion as
Then
![]() $x_n \in \mathcal {D}(x_0)$
and
$x_n \in \mathcal {D}(x_0)$
and
![]() $|x_n -x| \to 0$
as
$|x_n -x| \to 0$
as
![]() $n \to \infty $
. Hence,
$n \to \infty $
. Hence,
![]() $\mathcal {D}(x_0)$
is dense in
$\mathcal {D}(x_0)$
is dense in
![]() $\mathbb {I}$
, and so is
$\mathbb {I}$
, and so is
![]() $E(\gamma )$
.
$E(\gamma )$
.
For
![]() $\gamma \in (0,\infty )$
, let
$\gamma \in (0,\infty )$
, let
 $$ \begin{align*} E_*(\gamma):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq \gamma\bigg\} \end{align*} $$
$$ \begin{align*} E_*(\gamma):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \leq \gamma\bigg\} \end{align*} $$
and
 $$ \begin{align*} E^*(\gamma):=\bigg\{x\in \mathbb{I}: \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \geq \gamma\bigg\}. \end{align*} $$
$$ \begin{align*} E^*(\gamma):=\bigg\{x\in \mathbb{I}: \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} \geq \gamma\bigg\}. \end{align*} $$
We show that
![]() $E_*(\gamma )$
and
$E_*(\gamma )$
and
![]() $E^*(\gamma )$
are
$E^*(\gamma )$
are
![]() $G_\delta $
sets. To see this, we need the following notation. For
$G_\delta $
sets. To see this, we need the following notation. For
![]() $(a_1,\ldots ,a_n) \in \mathbb {N}^n$
, let
$(a_1,\ldots ,a_n) \in \mathbb {N}^n$
, let
It follows from Theorem 1.2.2 in [Reference Iosifescu and Kraaikamp16] that
![]() $I_{n}(a_1,\ldots , a_n) \cap \mathbb {I}$
is an open interval with rational endpoints in
$I_{n}(a_1,\ldots , a_n) \cap \mathbb {I}$
is an open interval with rational endpoints in
![]() $\mathbb {I}$
.
$\mathbb {I}$
.
Lemma 3.2. For any
![]() $\gamma \in (0,\infty )$
,
$\gamma \in (0,\infty )$
,
![]() $E_*(\gamma )$
and
$E_*(\gamma )$
and
![]() $E^*(\gamma )$
are
$E^*(\gamma )$
are
![]() $G_\delta $
sets.
$G_\delta $
sets.
Proof. Let
![]() $\gamma \in (0,\infty )$
be fixed. For
$\gamma \in (0,\infty )$
be fixed. For
![]() $E_*(\gamma )$
, we see that
$E_*(\gamma )$
, we see that
 $$ \begin{align} E_*(\gamma)=\bigcap_{k=1}^\infty\bigcap_{N=1}^\infty\bigcup_{n=N}^\infty E_n(\gamma, k), \end{align} $$
$$ \begin{align} E_*(\gamma)=\bigcap_{k=1}^\infty\bigcap_{N=1}^\infty\bigcup_{n=N}^\infty E_n(\gamma, k), \end{align} $$
where
![]() $E_n(\gamma , k)$
is given by
$E_n(\gamma , k)$
is given by
Note that each
![]() $E_n(\gamma , k)$
can be written as a countable union of open sets in
$E_n(\gamma , k)$
can be written as a countable union of open sets in
![]() $\mathbb {I}$
. More precisely,
$\mathbb {I}$
. More precisely,
 $$ \begin{align*} E_n(\gamma, k) = \bigcup_{i=1}^{\lfloor n^{\gamma +1/k}\rfloor}\bigcup_{j=1}^{{(\lfloor n^{\gamma +1/k}\rfloor-1)}/{i}}\bigcup_{(\sigma_1,\ldots,\sigma_{n-1})\in \mathbb{N}^{n-1}} I_{n+1}(\sigma_1,\ldots,\sigma_{n-1}, i , j) \cap \mathbb{I}. \end{align*} $$
$$ \begin{align*} E_n(\gamma, k) = \bigcup_{i=1}^{\lfloor n^{\gamma +1/k}\rfloor}\bigcup_{j=1}^{{(\lfloor n^{\gamma +1/k}\rfloor-1)}/{i}}\bigcup_{(\sigma_1,\ldots,\sigma_{n-1})\in \mathbb{N}^{n-1}} I_{n+1}(\sigma_1,\ldots,\sigma_{n-1}, i , j) \cap \mathbb{I}. \end{align*} $$
Since
![]() $I_{n+1}(\sigma _1,\ldots ,\sigma _{n-1},i,j) \cap \mathbb {I}$
is an open set in
$I_{n+1}(\sigma _1,\ldots ,\sigma _{n-1},i,j) \cap \mathbb {I}$
is an open set in
![]() $\mathbb {I}$
, it follows that
$\mathbb {I}$
, it follows that
![]() $E_n(\gamma , k)$
is open in
$E_n(\gamma , k)$
is open in
![]() $\mathbb {I}$
. By (3.1), we see that
$\mathbb {I}$
. By (3.1), we see that
![]() $E_*(\gamma )$
is a
$E_*(\gamma )$
is a
![]() $G_\delta $
set.
$G_\delta $
set.
For
![]() $E^*(\gamma )$
, since
$E^*(\gamma )$
, since
 $$ \begin{align*} E^*(\gamma)=\bigcap_{k=\lfloor1/\gamma\rfloor+1}^\infty\bigcap_{N=1}^\infty\bigcup_{n=N}^\infty \{x\in \mathbb{I}: a_n(x)a_{n+1}(x)> n^{\alpha -1/k}\}, \end{align*} $$
$$ \begin{align*} E^*(\gamma)=\bigcap_{k=\lfloor1/\gamma\rfloor+1}^\infty\bigcap_{N=1}^\infty\bigcup_{n=N}^\infty \{x\in \mathbb{I}: a_n(x)a_{n+1}(x)> n^{\alpha -1/k}\}, \end{align*} $$
and
![]() $\{x\in \mathbb {I}: a_n(x)a_{n+1}(x)> n^{\alpha -1/k}\}$
is a countable union of open sets in
$\{x\in \mathbb {I}: a_n(x)a_{n+1}(x)> n^{\alpha -1/k}\}$
is a countable union of open sets in
![]() $\mathbb {I}$
, we deduce that
$\mathbb {I}$
, we deduce that
![]() $E^*(\gamma )$
is a
$E^*(\gamma )$
is a
![]() $G_\delta $
set.
$G_\delta $
set.
Proof of Theorem 1.2.
For any
![]() $K \in \mathbb {N}$
, it follows from Lemmas 3.1 and 3.2 that
$K \in \mathbb {N}$
, it follows from Lemmas 3.1 and 3.2 that
![]() $E_*(1/K)$
and
$E_*(1/K)$
and
![]() $E^*(K)$
are residual. By the definition of a residual set, the countable intersection of residual sets is also residual. Since
$E^*(K)$
are residual. By the definition of a residual set, the countable intersection of residual sets is also residual. Since
 $$ \begin{align} \bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=0\bigg\} = \bigcap^\infty_{K=1}E_*(1/K) \end{align} $$
$$ \begin{align} \bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=0\bigg\} = \bigcap^\infty_{K=1}E_*(1/K) \end{align} $$
and
 $$ \begin{align} \bigg\{x\in \mathbb{I}: \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}=\infty\bigg\} = \bigcap^\infty_{K=1}E^*(K), \end{align} $$
$$ \begin{align} \bigg\{x\in \mathbb{I}: \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}=\infty\bigg\} = \bigcap^\infty_{K=1}E^*(K), \end{align} $$
the sets on the right-hand side of (3.2) and (3.3) are residual, and then their intersection
![]() $E(0,\infty )$
is residual.
$E(0,\infty )$
is residual.
We recall that every subset of a set of first category is also of first category. For
![]() $\alpha>0$
or
$\alpha>0$
or
![]() $\beta <\infty $
, each set
$\beta <\infty $
, each set
![]() $E(\alpha ,\beta )$
is a subset of the complement of
$E(\alpha ,\beta )$
is a subset of the complement of
![]() $E(0,\infty )$
, and hence
$E(0,\infty )$
, and hence
![]() $E(\alpha ,\beta )$
is of first category.
$E(\alpha ,\beta )$
is of first category.
Remark 3.3. For
![]() $\alpha , \beta \in [0,\infty ]$
with
$\alpha , \beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
, let
$\alpha \leq \beta $
, let
 $$ \begin{align*} F(\alpha,\beta):= \bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log q_n(x)}=\alpha,\ \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log q_n(x)}=\beta\bigg\}. \end{align*} $$
$$ \begin{align*} F(\alpha,\beta):= \bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log q_n(x)}=\alpha,\ \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log q_n(x)}=\beta\bigg\}. \end{align*} $$
Then
![]() $F(\alpha ,\beta )$
is concerned with the relative growth rate of the product of partial quotients. Corollary 3.7 of Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] shows that
$F(\alpha ,\beta )$
is concerned with the relative growth rate of the product of partial quotients. Corollary 3.7 of Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh17] shows that
![]() $F(0,1)$
has full Lebesgue measure. Feng and Xu [Reference Feng and Xu11] obtained the Hausdorff dimension of
$F(0,1)$
has full Lebesgue measure. Feng and Xu [Reference Feng and Xu11] obtained the Hausdorff dimension of
![]() $F(\alpha ,\beta )$
for all
$F(\alpha ,\beta )$
for all
![]() $\alpha , \beta \in [0,\infty ]$
with
$\alpha , \beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
. For the Baire category, following the method in this section, we conclude that
$\alpha \leq \beta $
. For the Baire category, following the method in this section, we conclude that
![]() $F(\alpha ,\beta )$
is residual if and only if
$F(\alpha ,\beta )$
is residual if and only if
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\beta =\infty $
. In particular, the set
$\beta =\infty $
. In particular, the set
![]() $F(\alpha ,\alpha )$
considered in [Reference Huang and Wu12] is of first category.
$F(\alpha ,\alpha )$
considered in [Reference Huang and Wu12] is of first category.
4. Proof of Theorem 1.3
The proof of Theorem 1.3 is divided in two cases:
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\alpha>0$
.
$\alpha>0$
.
4.1. The case
 $\alpha =0$
$\alpha =0$
In this case, we prove that
![]() $\dim _{\mathrm {H}}E(\alpha ,\beta )=1$
. To this end, we need the following lemma.
$\dim _{\mathrm {H}}E(\alpha ,\beta )=1$
. To this end, we need the following lemma.
Let
![]() $\{n_k\}$
be a sequence of positive real numbers satisfying
$\{n_k\}$
be a sequence of positive real numbers satisfying
![]() $n_k/k \to \infty $
and
$n_k/k \to \infty $
and
![]() $n_{k+1}/n_k \to ~1$
as
$n_{k+1}/n_k \to ~1$
as
![]() $k \to \infty $
. Let
$k \to \infty $
. Let
![]() $\{u_k\}$
be a sequence of positive integers satisfying
$\{u_k\}$
be a sequence of positive integers satisfying
![]() $u_k \to \infty $
as
$u_k \to \infty $
as
![]() $k \to \infty $
. For
$k \to \infty $
. For
![]() $M\in \mathbb {N}$
, define
$M\in \mathbb {N}$
, define
The Hausdorff dimension of
![]() $E_M(\{n_k\}, \{u_k\})$
is obtained by Liao and Rams [Reference Liao and Rams19].
$E_M(\{n_k\}, \{u_k\})$
is obtained by Liao and Rams [Reference Liao and Rams19].
Lemma 4.1 [Reference Liao and Rams19, Lemma 2.2].
Let
![]() $\{n_k\}$
,
$\{n_k\}$
,
![]() $\{u_k\}$
and
$\{u_k\}$
and
![]() $E_M(\{n_k\}, \{u_k\})$
be defined as above. If
$E_M(\{n_k\}, \{u_k\})$
be defined as above. If
 $$ \begin{align} \lim_{k \to \infty} \frac{1}{n_k} \sum^k_{j=1}\log u_j =0, \end{align} $$
$$ \begin{align} \lim_{k \to \infty} \frac{1}{n_k} \sum^k_{j=1}\log u_j =0, \end{align} $$
then
We use Lemma 4.1 to show that
![]() $\dim _{\mathrm {H}}E(0,\beta )=1$
by choosing suitable sequences
$\dim _{\mathrm {H}}E(0,\beta )=1$
by choosing suitable sequences
![]() $\{n_k\}$
and
$\{n_k\}$
and
![]() $\{u_k\}$
according to the value of
$\{u_k\}$
according to the value of
![]() $\beta $
. For all
$\beta $
. For all
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $n_k:=k^2$
and
$n_k:=k^2$
and
 $$ \begin{align*} u_k:= \left\{\!\! \begin{array}{ll} \lfloor \log k\rfloor+1 & \text{for } \beta=0, \\ \lfloor k^{2\beta}\rfloor & \text{for } \beta \in (0,\infty), \\ \lfloor e^{\sqrt{k}}\rfloor & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
$$ \begin{align*} u_k:= \left\{\!\! \begin{array}{ll} \lfloor \log k\rfloor+1 & \text{for } \beta=0, \\ \lfloor k^{2\beta}\rfloor & \text{for } \beta \in (0,\infty), \\ \lfloor e^{\sqrt{k}}\rfloor & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
Then
![]() $\{n_k\}$
and
$\{n_k\}$
and
![]() $\{u_k\}$
satisfy condition (4.1). Moreover,
$\{u_k\}$
satisfy condition (4.1). Moreover,
![]() $E_M(\{n_k\}, \{u_k\})$
is a subset of
$E_M(\{n_k\}, \{u_k\})$
is a subset of
![]() $E(0,\beta )$
. For example, when
$E(0,\beta )$
. For example, when
![]() $\beta \in (0,\infty )$
, for any
$\beta \in (0,\infty )$
, for any
![]() $x\in E_M(\{n_k\}, \{u_k\})$
, we have
$x\in E_M(\{n_k\}, \{u_k\})$
, we have
![]() $a_{k^2}(x) = \lfloor k^{2\beta }\rfloor $
and
$a_{k^2}(x) = \lfloor k^{2\beta }\rfloor $
and
![]() $1\leq a_j(x) \leq M$
for all
$1\leq a_j(x) \leq M$
for all
![]() $j\neq k^2$
$j\neq k^2$
![]() $(k=1,2,\ldots )$
, which gives
$(k=1,2,\ldots )$
, which gives
 $$ \begin{align*} 0 \leq \liminf_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \lim_{k \to \infty} \frac{\log(a_{k^2+1}(x)a_{k^2+2}(x))}{\log (k^2+1)}=0 \end{align*} $$
$$ \begin{align*} 0 \leq \liminf_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \lim_{k \to \infty} \frac{\log(a_{k^2+1}(x)a_{k^2+2}(x))}{\log (k^2+1)}=0 \end{align*} $$
and
 $$ \begin{align*} \beta =\lim_{k \to \infty} \frac{\log(a_{k^2}(x)a_{k^2+1}(x))}{2\log k} \leq \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}\leq \beta, \end{align*} $$
$$ \begin{align*} \beta =\lim_{k \to \infty} \frac{\log(a_{k^2}(x)a_{k^2+1}(x))}{2\log k} \leq \limsup_{n \to \infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n}\leq \beta, \end{align*} $$
that is,
![]() $x\in E(0,\beta )$
. So
$x\in E(0,\beta )$
. So
![]() $\dim _{\mathrm {H}} E(0,\beta ) \geq \dim _{\mathrm {H}}E_M(\{n_k\}, \{u_k\})$
. Letting
$\dim _{\mathrm {H}} E(0,\beta ) \geq \dim _{\mathrm {H}}E_M(\{n_k\}, \{u_k\})$
. Letting
![]() $M\to \infty $
, it follows from Lemma 4.1 that
$M\to \infty $
, it follows from Lemma 4.1 that
![]() $\dim _{\mathrm {H}} E(0,\beta )=1$
.
$\dim _{\mathrm {H}} E(0,\beta )=1$
.
4.2. The case
 $\alpha>0$
$\alpha>0$
In this case, we prove that
![]() $\dim _{\mathrm {H}}E(\alpha ,\beta )=1/2$
. For the upper bound, note that
$\dim _{\mathrm {H}}E(\alpha ,\beta )=1/2$
. For the upper bound, note that
![]() $E(\alpha ,\beta )$
is a subset of
$E(\alpha ,\beta )$
is a subset of
![]() $\{x\in \mathbb {I}: a_n(x)a_{n+1}(x) \to \infty \text { as } n \to \infty \}$
whose Hausdorff dimension is
$\{x\in \mathbb {I}: a_n(x)a_{n+1}(x) \to \infty \text { as } n \to \infty \}$
whose Hausdorff dimension is
![]() $1/2$
(see [Reference Zhang24, Proposition 3.1]). Hence,
$1/2$
(see [Reference Zhang24, Proposition 3.1]). Hence,
![]() $\dim _{\mathrm {H}}E(\alpha ,\beta ) \leq 1/2$
.
$\dim _{\mathrm {H}}E(\alpha ,\beta ) \leq 1/2$
.
For the lower bound, we need the following lemma. Let
![]() $\{s_n\}$
be a sequence of positive real numbers such that
$\{s_n\}$
be a sequence of positive real numbers such that
![]() $s_n \to \infty $
as
$s_n \to \infty $
as
![]() $n \to \infty $
. Write
$n \to \infty $
. Write
Lemma 4.2 [Reference Liao and Rams19, Lemma 2.3].
Let
![]() $\{s_n\}$
and
$\{s_n\}$
and
![]() $F(\{s_n\})$
be defined as above. Then
$F(\{s_n\})$
be defined as above. Then
 $$ \begin{align*} \dim_{\mathrm{H}}F(\{s_n\})=\frac{1}{2+\eta}\quad \text{with } \eta:=\limsup\limits_{n\to\infty}\frac{\log s_{n+1}}{\log s_1 + \cdots +\log s_n}. \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}}F(\{s_n\})=\frac{1}{2+\eta}\quad \text{with } \eta:=\limsup\limits_{n\to\infty}\frac{\log s_{n+1}}{\log s_1 + \cdots +\log s_n}. \end{align*} $$
For all
![]() $n \geq 1$
, let
$n \geq 1$
, let
 $$ \begin{align*} s_n:= \left\{\!\! \begin{array}{ll} n^{{(\alpha+\beta+(-1)^{\lfloor n/2\rfloor}(\alpha-\beta))}/{4}} & \text{for}\ \beta<\infty, \\ n^{{(\alpha+\sqrt{n}+(-1)^{\lfloor n/2 \rfloor}(\alpha-\sqrt{n}))}/{4}} & \text{for}\ \beta=\infty. \end{array} \right. \end{align*} $$
$$ \begin{align*} s_n:= \left\{\!\! \begin{array}{ll} n^{{(\alpha+\beta+(-1)^{\lfloor n/2\rfloor}(\alpha-\beta))}/{4}} & \text{for}\ \beta<\infty, \\ n^{{(\alpha+\sqrt{n}+(-1)^{\lfloor n/2 \rfloor}(\alpha-\sqrt{n}))}/{4}} & \text{for}\ \beta=\infty. \end{array} \right. \end{align*} $$
Then
 $$ \begin{align*} s_n= \left\{\!\! \begin{array}{ll} n^{\alpha/2} & \text{if}\ n=4k, \\ n^{\alpha/2} & \text{if}\ n=4k+1, \\ n^{\beta/2} & \text{if}\ n=4k+2, \\ n^{\beta/2} & \text{if}\ n=4k+3, \end{array} (\beta<\infty) \right. \quad \text{and} \quad s_n= \left\{\!\! \begin{array}{ll} n^{\alpha/2} & \text{if}\ n=4k, \\ n^{\alpha/2} & \text{if}\ n=4k+1, \\ n^{\sqrt{n}/2} & \text{if}\ n=4k+2, \\ n^{\sqrt{n}/2} & \text{if}\ n=4k+3, \end{array} (\beta=\infty). \right. \end{align*} $$
$$ \begin{align*} s_n= \left\{\!\! \begin{array}{ll} n^{\alpha/2} & \text{if}\ n=4k, \\ n^{\alpha/2} & \text{if}\ n=4k+1, \\ n^{\beta/2} & \text{if}\ n=4k+2, \\ n^{\beta/2} & \text{if}\ n=4k+3, \end{array} (\beta<\infty) \right. \quad \text{and} \quad s_n= \left\{\!\! \begin{array}{ll} n^{\alpha/2} & \text{if}\ n=4k, \\ n^{\alpha/2} & \text{if}\ n=4k+1, \\ n^{\sqrt{n}/2} & \text{if}\ n=4k+2, \\ n^{\sqrt{n}/2} & \text{if}\ n=4k+3, \end{array} (\beta=\infty). \right. \end{align*} $$
We see that
![]() $n^{\alpha /2} \leq s_n \leq n^{\beta /2}$
for
$n^{\alpha /2} \leq s_n \leq n^{\beta /2}$
for
![]() $\beta <\infty $
and
$\beta <\infty $
and
![]() $n^{\alpha /2} \leq s_n \leq n^{\sqrt {n}/2}$
for
$n^{\alpha /2} \leq s_n \leq n^{\sqrt {n}/2}$
for
![]() $\beta =\infty $
. Hence, in both cases, we have
$\beta =\infty $
. Hence, in both cases, we have
![]() $\eta =0$
. We also claim that
$\eta =0$
. We also claim that
![]() $F(\{s_n\})$
is a subset of
$F(\{s_n\})$
is a subset of
![]() $E(\alpha ,\beta )$
. For example, for
$E(\alpha ,\beta )$
. For example, for
![]() $x\in F(\{s_n\})$
, when
$x\in F(\{s_n\})$
, when
![]() $\beta <\infty $
,
$\beta <\infty $
,
 $$ \begin{align*} \alpha \leq \liminf_{n \to\infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \limsup_{n \to\infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \beta. \end{align*} $$
$$ \begin{align*} \alpha \leq \liminf_{n \to\infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \limsup_{n \to\infty} \frac{\log(a_n(x)a_{n+1}(x))}{\log n} \leq \beta. \end{align*} $$
Note that
 $$ \begin{align*} \lim_{k\to \infty} \frac{\log(a_{4k}(x)a_{4k+1}(x))}{\log (4k)}=\alpha\quad \text{and} \quad \lim_{k\to \infty} \frac{\log(a_{4k+2}(x)a_{4k+3}(x))}{\log (4k+2)}=\beta, \end{align*} $$
$$ \begin{align*} \lim_{k\to \infty} \frac{\log(a_{4k}(x)a_{4k+1}(x))}{\log (4k)}=\alpha\quad \text{and} \quad \lim_{k\to \infty} \frac{\log(a_{4k+2}(x)a_{4k+3}(x))}{\log (4k+2)}=\beta, \end{align*} $$
so
 $$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = \alpha\quad \text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\beta, \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n} = \alpha\quad \text{and}\quad \limsup_{n \to \infty} \frac{\log (a_n(x)a_{n+1}(x))}{\log n}=\beta, \end{align*} $$
that is,
![]() $x\in E(\alpha ,\beta )$
. By Lemma 4.2,
$x\in E(\alpha ,\beta )$
. By Lemma 4.2,
![]() $\dim _{\mathrm {H}} E(\alpha ,\beta ) \geq \dim _{\mathrm {H}}F(\{s_n\}) = 1/(2+\eta ) =1/2$
. This gives the desired lower bound.
$\dim _{\mathrm {H}} E(\alpha ,\beta ) \geq \dim _{\mathrm {H}}F(\{s_n\}) = 1/(2+\eta ) =1/2$
. This gives the desired lower bound.
5. Weighted products of consecutive partial quotients
Our results can be extended to the setting of weighted products of consecutive partial quotients. For a fixed integer
![]() $m \geq 2$
and a weight vector
$m \geq 2$
and a weight vector
![]() $\mathbf {t}=(t_0,\ldots ,t_{m-1}) \in \mathbb {R}^m_+$
, let
$\mathbf {t}=(t_0,\ldots ,t_{m-1}) \in \mathbb {R}^m_+$
, let
 $$ \begin{align*} W^{\mathbf{t}}_n(x):= \prod^{m-1}_{i=0}a^{t_i}_{n+i}(x). \end{align*} $$
$$ \begin{align*} W^{\mathbf{t}}_n(x):= \prod^{m-1}_{i=0}a^{t_i}_{n+i}(x). \end{align*} $$
The following zero-one law for
![]() $W^{\mathbf {t}}_n(x)$
, established by Bakhtawar et al. [Reference Bakhtawar, Hussain, Kleinbock and Wang4], is helpful for obtaining the limsup behaviour of
$W^{\mathbf {t}}_n(x)$
, established by Bakhtawar et al. [Reference Bakhtawar, Hussain, Kleinbock and Wang4], is helpful for obtaining the limsup behaviour of
![]() $W^{\mathbf {t}}_n(x)$
.
$W^{\mathbf {t}}_n(x)$
.
For any function
![]() $\Psi :\mathbb {N} \to (1,\infty )$
, let
$\Psi :\mathbb {N} \to (1,\infty )$
, let
Theorem 5.1 [Reference Bakhtawar, Hussain, Kleinbock and Wang4, Theorem 1.4].
Denote
Then
 $$ \begin{align*} \mathcal{L}(\mathcal{E}_{\mathbf{t}}(\Psi)) = \begin{cases} 0 & \displaystyle\text{if } \sum^\infty_{n=1}{(\log\Psi(n))^{\ell -1}}/{(\Psi(n))^{1/t_{\max}}} <\infty, \\ 1 & \displaystyle\text{if } \sum^\infty_{n=1}{(\log\Psi(n))^{\ell -1}}/{(\Psi(n))^{1/t_{\max}}} =\infty. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{L}(\mathcal{E}_{\mathbf{t}}(\Psi)) = \begin{cases} 0 & \displaystyle\text{if } \sum^\infty_{n=1}{(\log\Psi(n))^{\ell -1}}/{(\Psi(n))^{1/t_{\max}}} <\infty, \\ 1 & \displaystyle\text{if } \sum^\infty_{n=1}{(\log\Psi(n))^{\ell -1}}/{(\Psi(n))^{1/t_{\max}}} =\infty. \end{cases} \end{align*} $$
Following the proof of Theorem 1.1 and applying Theorem 5.1, we derive the liminf and limsup behaviours of
![]() $\log W^{\mathbf {t}}_n(x)$
.
$\log W^{\mathbf {t}}_n(x)$
.
Theorem 5.2. For Lebesgue almost all
![]() $x\in \mathbb {I},$
$x\in \mathbb {I},$
 $$ \begin{align*} \liminf_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n} = 0 \quad\text{and}\quad \limsup_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=t_{\max}. \end{align*} $$
$$ \begin{align*} \liminf_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n} = 0 \quad\text{and}\quad \limsup_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=t_{\max}. \end{align*} $$
In what follows, we study the Baire category and the Hausdorff dimension of
![]() $W^{\mathbf {t}}_n(x)$
. For any
$W^{\mathbf {t}}_n(x)$
. For any
![]() $\alpha ,\beta \in [0,\infty ]$
with
$\alpha ,\beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta $
, let
$\alpha \leq \beta $
, let
 $$ \begin{align*} E_{\mathbf{t}}(\alpha,\beta):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=\alpha,\ \limsup_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=\beta\bigg\}. \end{align*} $$
$$ \begin{align*} E_{\mathbf{t}}(\alpha,\beta):=\bigg\{x\in \mathbb{I}: \liminf_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=\alpha,\ \limsup_{n \to \infty} \frac{\log W^{\mathbf{t}}_n(x)}{\log n}=\beta\bigg\}. \end{align*} $$
The method in Section 3 gives the necessary and sufficient conditions for
![]() $E_{\mathbf {t}}(\alpha ,\beta )$
to be residual.
$E_{\mathbf {t}}(\alpha ,\beta )$
to be residual.
Theorem 5.3. The set
![]() $E_{\mathbf {t}}(\alpha ,\beta )$
is residual if and only if
$E_{\mathbf {t}}(\alpha ,\beta )$
is residual if and only if
![]() $\alpha =0$
and
$\alpha =0$
and
![]() $\beta =\infty $
.
$\beta =\infty $
.
The Hausdorff dimension of
![]() $E_{\mathbf {t}}(\alpha ,\beta )$
is the same as that of
$E_{\mathbf {t}}(\alpha ,\beta )$
is the same as that of
![]() $E(\alpha ,\beta )$
.
$E(\alpha ,\beta )$
.
Theorem 5.4. For
![]() $\alpha , \beta \in [0,\infty ]$
with
$\alpha , \beta \in [0,\infty ]$
with
![]() $\alpha \leq \beta, $
$\alpha \leq \beta, $
 $$ \begin{align*} \dim_{\mathrm{H}} E_{\mathbf{t}}(\alpha,\beta) = \left\{\!\! \begin{array}{ll} 1 & \text{for } \alpha=0,\\ \frac{1}{2} & \text{for } \alpha>0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \dim_{\mathrm{H}} E_{\mathbf{t}}(\alpha,\beta) = \left\{\!\! \begin{array}{ll} 1 & \text{for } \alpha=0,\\ \frac{1}{2} & \text{for } \alpha>0. \end{array} \right. \end{align*} $$
Proof. Following the proof of Theorem 1.3 step by step, the proof can be completed by changing the form of
![]() $u_k$
in the case
$u_k$
in the case
![]() $\alpha =0$
and the form of
$\alpha =0$
and the form of
![]() $s_n$
in the case
$s_n$
in the case
![]() $\alpha>0$
. To see this, fix an integer
$\alpha>0$
. To see this, fix an integer
![]() $m \geq 2$
and a weight vector
$m \geq 2$
and a weight vector
![]() $\mathbf {t}=(t_0,\ldots ,t_{m-1}) \in \mathbb {R}^m_+$
.
$\mathbf {t}=(t_0,\ldots ,t_{m-1}) \in \mathbb {R}^m_+$
.
For the case
![]() $\alpha =0$
, let
$\alpha =0$
, let
![]() $n_k:=k^2$
and
$n_k:=k^2$
and
 $$ \begin{align*} u_k:= \left\{\!\! \begin{array}{ll} \lfloor \log k\rfloor+1 & \text{for } \beta=0, \\ \lfloor k^{2\beta/t_{\max}}\rfloor & \text{for } \beta \in (0,\infty), \\ \lfloor e^{\sqrt{k}}\rfloor & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
$$ \begin{align*} u_k:= \left\{\!\! \begin{array}{ll} \lfloor \log k\rfloor+1 & \text{for } \beta=0, \\ \lfloor k^{2\beta/t_{\max}}\rfloor & \text{for } \beta \in (0,\infty), \\ \lfloor e^{\sqrt{k}}\rfloor & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
Then
![]() $E_M(\{n_k\}, \{u_k\})$
is a subset of
$E_M(\{n_k\}, \{u_k\})$
is a subset of
![]() $E_{\mathbf {t}}(0,\beta )$
for all
$E_{\mathbf {t}}(0,\beta )$
for all
![]() $M\in \mathbb {N}$
. It follows from Lemma 4.1 that
$M\in \mathbb {N}$
. It follows from Lemma 4.1 that
![]() $E_{\mathbf {t}}(0,\beta )$
has full Hausdorff dimension.
$E_{\mathbf {t}}(0,\beta )$
has full Hausdorff dimension.
For the case
![]() $\alpha>0$
, let
$\alpha>0$
, let
 $$ \begin{align*} s_n:= \left\{\!\! \begin{array}{ll} n^{{(\alpha+\beta+(-1)^{\lfloor n/m\rfloor}(\alpha-\beta))}/{2(t_0+\cdots+t_{m-1})}} & \text{for } \beta<\infty, \\ n^{{(\alpha+\sqrt{n}+(-1)^{\lfloor n/m \rfloor}(\alpha-\sqrt{n}))}/{2(t_0+\cdots+t_{m-1})}} & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
$$ \begin{align*} s_n:= \left\{\!\! \begin{array}{ll} n^{{(\alpha+\beta+(-1)^{\lfloor n/m\rfloor}(\alpha-\beta))}/{2(t_0+\cdots+t_{m-1})}} & \text{for } \beta<\infty, \\ n^{{(\alpha+\sqrt{n}+(-1)^{\lfloor n/m \rfloor}(\alpha-\sqrt{n}))}/{2(t_0+\cdots+t_{m-1})}} & \text{for } \beta=\infty. \end{array} \right. \end{align*} $$
Then
![]() $\eta =0$
and
$\eta =0$
and
![]() $F(\{s_n\})$
is a subset of
$F(\{s_n\})$
is a subset of
![]() $E_{\mathbf {t}}(\alpha ,\beta )$
. Further,
$E_{\mathbf {t}}(\alpha ,\beta )$
. Further,
![]() $\dim_H E_{\bf t}(\alpha,\beta) \ge 1/(2+\eta) = 1/2$
by Lemma 4.2. For the upper bound, let
$\dim_H E_{\bf t}(\alpha,\beta) \ge 1/(2+\eta) = 1/2$
by Lemma 4.2. For the upper bound, let
![]() $W^{\mathbf {t}}:=\{x\in \mathbb {I}: W^{\mathbf {t}}_n(x) \to \infty \text { as } n \to \infty \}$
. Then
$W^{\mathbf {t}}:=\{x\in \mathbb {I}: W^{\mathbf {t}}_n(x) \to \infty \text { as } n \to \infty \}$
. Then
![]() $E_{\mathbf {t}}(\alpha ,\beta )$
is a subset of
$E_{\mathbf {t}}(\alpha ,\beta )$
is a subset of
![]() $W^{\mathbf {t}}$
. Moreover, we remark that the Hausdorff dimension of
$W^{\mathbf {t}}$
. Moreover, we remark that the Hausdorff dimension of
![]() $W^{\mathbf {t}}$
is at most one-half. To see this, note that
$W^{\mathbf {t}}$
is at most one-half. To see this, note that
![]() $W^{\mathbf {t}} \times \mathbb I$
is a subset of the set of
$W^{\mathbf {t}} \times \mathbb I$
is a subset of the set of
![]() $(x,y)\in \mathbb I\times \mathbb I$
for which
$(x,y)\in \mathbb I\times \mathbb I$
for which
![]() $\max \{W^{\mathbf {t}}_n(x), W^{\mathbf {t}}_n(y)\}\to \infty $
as
$\max \{W^{\mathbf {t}}_n(x), W^{\mathbf {t}}_n(y)\}\to \infty $
as
![]() $n \to \infty $
, where
$n \to \infty $
, where
![]() $E\times F$
denotes the Cartesian product of E and F. We deduce from [Reference Brown-Sarre and Hussain6, Proposition 3.1] that the latter has Hausdorff dimension
$E\times F$
denotes the Cartesian product of E and F. We deduce from [Reference Brown-Sarre and Hussain6, Proposition 3.1] that the latter has Hausdorff dimension
![]() $3/2$
. It follows from the Product Formula 7.2 in [Reference Falconer9, page 101] that the Hausdorff dimension of
$3/2$
. It follows from the Product Formula 7.2 in [Reference Falconer9, page 101] that the Hausdorff dimension of
![]() $W^{\mathbf {t}} \times \mathbb I$
is at least
$W^{\mathbf {t}} \times \mathbb I$
is at least
![]() $1+\dim _{\mathrm {H}} W^{\mathbf {t}}$
. Thus, the Hausdorff dimension of
$1+\dim _{\mathrm {H}} W^{\mathbf {t}}$
. Thus, the Hausdorff dimension of
![]() $W^{\mathbf {t}}$
is at most
$W^{\mathbf {t}}$
is at most
![]() $1/2$
. Hence,
$1/2$
. Hence,
![]() $\dim _{\mathrm {H}} E_{\mathbf {t}}(\alpha ,\beta ) \leq \dim _{\mathrm {H}} W^{\mathbf {t}} \leq 1/2$
.
$\dim _{\mathrm {H}} E_{\mathbf {t}}(\alpha ,\beta ) \leq \dim _{\mathrm {H}} W^{\mathbf {t}} \leq 1/2$
.
Acknowledgement
The authors would like to thank the anonymous referee for the valuable comments and suggestions that allowed us to greatly improve the quality of the manuscript.