Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T20:14:07.077Z Has data issue: false hasContentIssue false
  • English
  • Français

ARITHMETIC PROPERTIES OF 1-SHELL TOTALLY SYMMETRIC PLANE PARTITIONS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  27 September 2013

MICHAEL D. HIRSCHHORN  and
JAMES A. SELLERS
MICHAEL D. HIRSCHHORN
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney 2052, Australia email [email protected]
JAMES A. SELLERS*
Affiliation:
Department of Mathematics, Penn State University, University Park, PA 16802, USA
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Blecher [‘Geometry for totally symmetric plane partitions (TSPPs) with self-conjugate main diagonal’, Util. Math. 88 (2012), 223–235] defined the combinatorial objects known as 1-shell totally symmetric plane partitions of weight $n$. He also proved that the generating function for 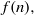$f(n), $ the number of 1-shell totally symmetric plane partitions of weight $n$, is given by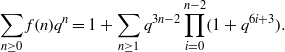

$$\begin{eqnarray*}\displaystyle \sum _{n\geq 0}f(n){q}^{n} = 1+ \sum _{n\geq 1}{q}^{3n- 2} \prod _{i= 0}^{n- 2} (1+ {q}^{6i+ 3} ).\end{eqnarray*}$$
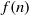In this brief note, we prove a number of arithmetic properties satisfied by $f(n)$ using elementary generating function manipulations and well-known results of Ramanujan and Watson.

Keywords

partitiontotally symmetric plane partitionTSPPgenerating functioncongruence

MSC classification

Secondary: 05A17: Partitions of integers 11P83: Partitions; congruences and congruential restrictions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 473 - 478
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., The Theory of Partitions (Addison-Wesley, Reading, MA, 1976) (reprinted Cambridge University Press, Cambridge, 1984, 1998).Google Scholar
Andrews, G. E. and Berndt, B. C., Ramanujan’s Lost Notebook, Part I (Springer, New York, 2005).CrossRefGoogle Scholar
Andrews, G. E., Paule, P. and Schneider, C., ‘Plane partitions VI: Stembridge’s TSPP theorem’, Adv. Appl. Math. 34 (4) (2005), 709–739.CrossRefGoogle Scholar
Blecher, A., ‘Geometry for totally symmetric plane partitions (TSPPs) with self-conjugate main diagonal’, Util. Math. 88 (2012), 223–235.Google Scholar
Fine, N. J., Basic Hypergeometric Series and Applications, Mathematical Surveys and Monographs, 27 (American Mathematical Society, Providence, RI, 1988).CrossRefGoogle Scholar
Hirschhorn, M. D., ‘Another short proof of Ramanujan’s mod 5 partition congruence, and more’, Amer. Math. Monthly 106 (6) (1999), 580–583.CrossRefGoogle Scholar
Stembridge, J. R., ‘The enumeration of totally symmetric plane partitions’, Adv. Math. 111 (2) (1995), 227–243.CrossRefGoogle Scholar