Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T07:27:17.423Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ANNIHILATOR OF TENSOR SPACE IN THE 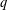$q$-ROOK MONOID ALGEBRA

Part of: Representation theory of groups Linear algebraic groups and related topics Algebraic combinatorics Semigroups

Published online by Cambridge University Press:  02 March 2017

ZHANKUI XIAO
ZHANKUI XIAO*
Affiliation:
School of Mathematical Sciences, Huaqiao University, Quanzhou, Fujian, 362021, P. R. China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we give an explicit construction of a quasi-idempotent in the 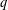$q$-rook monoid algebra 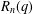$R_{n}(q)$ and show that it generates the whole annihilator of the tensor space 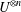$U^{\otimes n}$ in 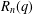$R_{n}(q)$.

Keywords

tensor spaceq-rook monoidSchur–Weyl duality

MSC classification

Primary: 20C08: Hecke algebras and their representations
Secondary: 05E10: Combinatorial aspects of representation theory 20G05: Representation theory 20M30: Representation of semigroups; actions of semigroups on sets
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 77 - 86
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Dieng, M., Halverson, T. and Poladian, V., ‘Character formulas for q-rook monoid algebras’, J. Algebraic Combin. 17 (2003), 99–123.Google Scholar
East, J., ‘Cellular algebras and inverse semigroups’, J. Algebra 296 (2006), 505–519.Google Scholar
Graham, J. J. and Lehrer, G. I., ‘Cellular algebras’, Invent. Math. 123 (1996), 1–34.Google Scholar
Grood, C., ‘A Specht module analog for the rook monoid’, Electron. J. Combin. 9 (2002), Article ID #R2, 10 pages.Google Scholar
Halverson, T., ‘Representations of the q-rook monoid’, J. Algebra 273 (2004), 227–251.CrossRefGoogle Scholar
Halverson, T. and Ram, A., ‘ q-rook monoid algebras, Hecke algebras, and Schur–Weyl duality’, J. Math. Sci. 121 (2004), 2419–2436; translated from Zap. Nauch. Sem. POMI 283 (2001), 224–250.Google Scholar
Hu, J., ‘Schur–Weyl reciprocity between quantum groups and Hecke algebras of type G (r, 1, n)’, Math. Z. 238 (2001), 505–521.Google Scholar
Hu, J. and Xiao, Z.-K., ‘On tensor spaces for Birman–Murakami–Wenzl algebras’, J. Algebra 324 (2010), 2893–2922.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., ‘Strongly multiplicity free modules for Lie algebras and quantized groups’, J. Algebra 306 (2006), 138–174.CrossRefGoogle Scholar
Lehrer, G. I. and Zhang, R. B., ‘The second fundamental theorem of invariant theory for the orthogonal group’, Ann. of Math. (2) 176 (2012), 2031–2054.Google Scholar
Lehrer, G. I. and Zhang, R. B., ‘The Brauer category and invariant theory’, J. Eur. Math. Soc. (JEMS) 17 (2015), 2311–2351.CrossRefGoogle Scholar
Mathas, A., Iwahori–Hecke algebras and Schur algebras of the symmetric group, University Lecture Series, 15 (Amreican Mathematical Society, Providence, RI, 1999).Google Scholar
Paget, R., ‘Representation theory of q-rook monoid algebras’, J. Algebraic Combin. 24 (2006), 239–252.Google Scholar
Sakamoto, S. and Shoji, T., ‘Schur–Weyl reciprocity for Ariki–Koike algebras’, J. Algebra 221 (1999), 293–314.Google Scholar
Solomon, L., ‘The Bruhat decomposition, Tits system and Iwahori ring for the monoid of matrices over a finite field’, Geom. Dedicata 36 (1990), 15–49.Google Scholar
Solomon, L., ‘Representations of the rook monoid’, J. Algebra 256 (2002), 309–342.CrossRefGoogle Scholar
Solomon, L., ‘The Iwahori algebra of M n (F q ), a presentation and a representation on tensor space’, J. Algebra 273 (2004), 206–226.Google Scholar
Xiao, Z.-K., ‘On tensor spaces for rook monoid algebras’, Acta Math. Sinica, English Series 32 (2016), 607–620.Google Scholar