Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-07T22:55:16.123Z Has data issue: false hasContentIssue false
  • English
  • Français

An extension of kesten's generalised law of the iterated Logarithm

Published online by Cambridge University Press:  17 April 2009

R. A. Maller
R. A. Maller
Affiliation:
Division of Mathematics and Statistics, CSIRO, Private Bag, PO Wembley, Western Australia 6014, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Xi be independent and identically distributed random variables with Sn = X1 + X2 + … + Xn. We extend a classic result of Kesten, by showing that if Xiare in the domain of partial attraction of the normal distribution, there are sequences αn and B(n) for which

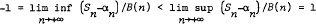
almost surely, and the almost sure limit points of (sn−αn)/b(n) coincide with the interval [−1, l]. The norming sequence B(n) is slightly different to that used by Kesten, and has properties that are less desirable. The converse to the above result is known to be true by results of Heyde and Rogozin.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 21 , Issue 3 , June 1980 , pp. 393 - 406
Copyright
Copyright © Australian Mathematical Society 1980

References

[1]Feller, William, An introduction to probability theory and its applications. Volume II, second edition (John Wiley & Sons, New York, London, Sydney, 1971).Google Scholar
[2]Heyde, C.C., “A note concerning behaviour of iterated logarithm type”, Proc. Amer. Math. Soc. 23 (1969), 85–90.CrossRefGoogle Scholar
[3]Kesten, Harry, “The limit points of a normalized random walk”, Ann. Math. Statist. 41 (1970), 1173–1205.CrossRefGoogle Scholar
[4]Kesten, Harry, “Sums of independent random variables – without moment conditions”, Ann. Math. Statist. 43 (1972), 701–732.CrossRefGoogle Scholar
[5]Lévy, Paul, Théorie de I'addition des variables alèatoires (Gauthier–Villars, Paris, 1937).Google Scholar
[6]Lofève, M., Probability theory I, 4th edition (Graduate Texts in Mathematics, 45. Springer-Verlag, New York, Heidelberg, Berlin, 1977).Google Scholar
[7]Petrov, V.V., “A generalization of an inequality of Levy”, Theor. Prob. Appl. 20 (1975), 141–145.CrossRefGoogle Scholar
[8]Rogozin, B.A., “On the existence of exact upper sequences”, Theor. Prob. Appl. 13 (1968), 667–672.CrossRefGoogle Scholar