No CrossRef data available.
Article contents
An asymptotic theorem for abstract differential equations
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we prove the existence of a continuous one-to-one correspondence between bounded solutions of the equation x′(t) = Ax(t) + b(t) which belong to a certain subclass L+ of 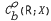 and bounded mild solutions of the equation x′(t) = Ax(t) + b(t) + f(t, x(t)) of the form u(t) = ø(t) + Ψ(t), with ø(t) ∈ L+ and
and bounded mild solutions of the equation x′(t) = Ax(t) + b(t) + f(t, x(t)) of the form u(t) = ø(t) + Ψ(t), with ø(t) ∈ L+ and 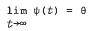 .
.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 33 , Issue 1 , February 1986 , pp. 139 - 144
- Copyright
- Copyright © Australian Mathematical Society 1986
References
[1]Coppel, W.A., Dichotomies in Stability Theory, (Springer-Verlag, Berlin-Heidelberg-New York, 1978.Google Scholar
[2]Fink, A.-M., Almost Periodic Differential Equations,(Springer-Verlag, Berlin-Heidelberg-New York, 1974 ).CrossRefGoogle Scholar
[3]Mishnaevskii, P.A., “The attainment of almost-periodic conditions and the almost-periodicity of solutions of differential equations in a Banach space”, Vestnik Moskov. Univ. Mat., 26 (3) (1971), 69–76.Google Scholar
[4]N'Guérékata, G.M., “Sur les solutions presque automorphes d'équations différentielles abstraites”, Ann. Sci. Math. Québec, V (1) (1981), 69–79.Google Scholar
[5]N'Guérékata, G.M., “Quelques remarques sur les fonctions asymptotiquement presque automorphes”, Ann. Sci. Math. Québec, VII (2) (1983), 185–191.Google Scholar
[6]Zaidman, S., “Notes on abstract almost-periodicity”, Riv. Mat. Univ. Parma, 5 (4) (1979), 837–845.Google Scholar
[7]Zaidman, S., Almost Periodic Functions in Abstract Spaces, (Pitman Advanced Publishing Program, Boston-London-Melbourne, 1985).Google Scholar


