Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T05:18:17.939Z Has data issue: false hasContentIssue false
  • English
  • Français

AN APPROACH TO CAPABLE GROUPS AND SCHUR’S THEOREM

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  05 May 2015

MITRA HASSANZADEH  and
RASOUL HATAMIAN
MITRA HASSANZADEH*
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran email [email protected]
RASOUL HATAMIAN
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159-91775, Mashhad, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

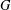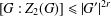Podoski and Szegedy [‘On finite groups whose derived subgroup has bounded rank’, Israel J. Math.178 (2010), 51–60] proved that for a finite group $G$ with rank $r$, the inequality $[G:Z_{2}(G)]\leq |G^{\prime }|^{2r}$ holds. In this paper we omit the finiteness condition on 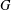$G$ and show that groups with finite derived subgroup satisfy the same inequality. We also construct an $n$-capable group which is not 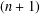$(n+1)$-capable for every 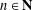$n\in \mathbf{N}$.

Keywords

derived subgroupSchur’s theoremn-isoclinismn-capable groups

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20E34: General structure theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 52 - 56
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Baer, R., ‘Endlichkeitskriterien für kommutatorgruppen’, Math. Ann. 124 (1952), 161–177.CrossRefGoogle Scholar
Burns, J. and Ellis, G., ‘On the nilpotent multipliers of a group’, Math. Z. 226 (1997), 405–428.CrossRefGoogle Scholar
Fernández-Alcober, G. A. and Morigi, M., ‘Generalizing a theorem of P. Hall on finite by nilpotent groups’, Proc. Amer. Math. Soc. 137(2) (2008), 425–429.CrossRefGoogle Scholar
Hall, P., ‘Finite-by-nilpotent groups’, Proc. Cambridge Philos. Soc. 52 (1956), 611–616.CrossRefGoogle Scholar
Hekster, N. S., ‘On the structure of n-isoclinism classes of groups’, J. Pure Appl. Algebra 40(1) (1986), 63–85.CrossRefGoogle Scholar
Macdonald, I. D., ‘Some explicit bounds in groups with finite derived groups’, Proc. Lond. Math. Soc. (3) 3(11) (1961), 23–56.CrossRefGoogle Scholar
Moghaddam, M. R. R. and Kayvanfar, S., ‘A new notion derived from varieties of groups’, Algebra Colloq. 4(1) (1997), 1–11.Google Scholar
Podoski, K. and Szegedy, B., ‘Bounds for the index of the centre in capable groups’, Proc. Amer. Math. Soc. 133 (2005), 3441–3445.CrossRefGoogle Scholar
Podoski, K. and Szegedy, B., ‘On finite groups whose derived subgroup has bounded rank’, Israel J. Math. 178 (2010), 51–60.CrossRefGoogle Scholar