Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-27T02:28:26.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost all normal sets are strictly normal

Published online by Cambridge University Press:  17 April 2009

Alexander J. Zaslavski
Alexander J. Zaslavski
Affiliation:
Department of Mathematics, The Technion-Israel Institute of Technology, 3200 Haifa, Israel, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the space Sn of all nonempty bounded closed normal subsets of the con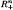e where 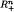is the set of all vectors x ∈ Rn with nonnegative coordinates. We equip the space Sn with the Hausdorff metric and show that most elements of Sn are, in fact, strictly normal. More precisely, we show that the complement of the collection of all stricly normal elements of Sn is a σ-porous subset of Sn.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 69 , Issue 1 , February 2004 , pp. 151 - 159
Copyright
Copyright © Australian Mathematical Society 2004

References

[1] Asplund, E., ‘Fréchet differentiability of convex functions’, Acta Math. 121 1968, 31–47.CrossRefGoogle Scholar
[2] Ball, J.M. and Nadirashvili, N.S., ‘Universal singular sets for one-dimensional variational problems’, Calc. Var. Partial Differential Equations 1 1993, 429–438.CrossRefGoogle Scholar
[3] Cellina, A. and Mariconda, C., ‘The existence question in the calculus of variations: A density result’, Proc. Amer. Math. soc. 120 1994, 1145–1150.Google Scholar
[4] De Blasi, F.S. and Myjak, J., ‘Sur la porosité des contractions sans point fixe’, C. R. Acad. Sci. Paris Ser. I 308 1989, 51–54.Google Scholar
[5] De Blasi, F.S. and Myjak, J., ‘On a generalized best approximation problem’, J. Approx. Theory 94 1998, 54–72.CrossRefGoogle Scholar
[6] Dzalilov, Z., Rubinov, A.M. and Kloeden, P.E., ‘Lyapunov sequences and a turnpike theorem without convexity’, Set-Valued Anal. 6 1998, 277–302.CrossRefGoogle Scholar
[7] Makarov, V.L., Levin, M.J. and Rubinov, A.M., Mathematical economic theory: Pure and mixed types of economic mechanisms (North-Holland, Amsterdam, 1995).Google Scholar
[8] Makarov, V.L. and Rubinov, A.M., Mathematical theory of economic dynamics and equilibria (Springer-Verlag, New York, 1977).Google Scholar
[9] Rubinov, A.M., Abstract convexity and global optimization (Kluwer Academic Publishers, Dordrecht, 2000).CrossRefGoogle Scholar
[10] Rubinov, A.M. and Singer, I., ‘Best approximation by normal and conormal sets’, J. Approx. Theory 107 2000, 212–243.CrossRefGoogle Scholar
[11] Rubinov, A.M. and Zaslavski, A.J., ‘Existence and uniqueness of a solution for a minimization problem with a generic increasing function’, J. Austral. Math. Society Ser. A 67 1999, 85–103.Google Scholar
[12] Rubinov, A.M. and Zaslavski, A.J., ‘Two porosity results in monotonic analysis’, Numer. Funct. Anal. Optim. 23 2002, 651–668.Google Scholar
[13] Stechkin, S.B., ‘Approximative properties of sets in normed linear spaces’, Rev. Roumaine Math. Pures Appl. 8 1963, 5–13.Google Scholar