Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T11:05:38.905Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC VALUES OF CERTAIN ANALYTIC FUNCTIONS DEFINED BY A CANONICAL PRODUCT

Part of: Entire and meromorphic functions, and related topics Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  08 October 2019

TABOKA P. CHALEBGWA Open the ORCID record for TABOKA P. CHALEBGWA [Opens in a new window]
TABOKA P. CHALEBGWA*
Affiliation:
The Fields Institute, 222 College Street, 3rd Floor, Toronto, Ontario M5T 3J1, Canada email [email protected] Department of Mathematical Sciences, Mathematics Division, Stellenbosch University, Private Bag X1, 7602 Matieland, South Africa
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a partial answer to a question attributed to Chris Miller on algebraic values of certain transcendental functions of order less than one. We obtain 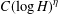$C(\log H)^{\unicode[STIX]{x1D702}}$ bounds for the number of algebraic points of height at most 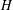$H$ on certain subsets of the graphs of such functions. The constant 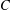$C$ and exponent 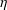$\unicode[STIX]{x1D702}$ depend on data associated with the functions and can be effectively computed from them.

Keywords

algebraic pointsbounded heighttranscendental functions

MSC classification

Primary: 11J99: None of the above, but in this section
Secondary: 30D20: Entire functions, general theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 415 - 425
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is based on the research supported in part by the National Research Foundation of South Africa (Grant Number 96234). The author was also supported by the South African National Research Foundation Innovation doctoral scholarship and a Fields-AIMS-Perimeter postdoctoral scholarship.

References

Besson, E., ‘Points rationnels de la fonction Gamma d’Euler’, Arch. Math. 1 (2014), 61–73.Google Scholar
Bombieri, E. and Pila, J., ‘The number of integral points on arcs and ovals’, Duke Math J. 59 (1989), 237–275.Google Scholar
Boxall, G. and Jones, G., ‘Algebraic values of certain analytic functions’, Int. Math. Res. Not. IMRN 2013(4) (2013), 1141–1158.Google Scholar
Boxall, G. and Jones, G., ‘Rational values of entire functions of finite order’, Int. Math. Res. Not. IMRN 2015(52) (2015), 12251–12264.Google Scholar
Goldberg, A. and Ostrovskii, I., Value Distribution of Meromorphic Functions, Translations of Mathematical Monographs, 236 (American Mathematical Society, Providence, RI, 2008).10.1090/mmono/236Google Scholar
Masser, D., ‘Rational values of the Riemann zeta function’, J. Number Theory 11 (2011), 2037–2046.Google Scholar
Pila, J., ‘Geometric postulation of a smooth function and the number of rational points’, Duke Math J. 63 (1991), 237–275.Google Scholar
Rahman, Q. I. and Schmeisser, G., Analytic Theory of Polynomials (Oxford University Press, New York, 2002).Google Scholar
Surroca, A., ‘Sur le nombre de points algébriques où une fonction analytique transcendante prend des valeurs algébriques’, C. R. Math. 334 (2002), 721–725.Google Scholar
Waldschmidt, M., Diophantine Approximation on Linear Algebraic Groups (Springer, Berlin, 2000).Google Scholar