Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T19:54:37.306Z Has data issue: false hasContentIssue false
  • English
  • Français

ALGEBRAIC SURFACES WITH INFINITELY MANY TWISTOR LINES

Part of: Global differential geometry Holomorphic fiber spaces Families, fibrations Generalized function theory Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  24 May 2019

A. ALTAVILLA Open the ORCID record for A. ALTAVILLA [Opens in a new window]  and
E. BALLICO Open the ORCID record for E. BALLICO [Opens in a new window]
A. ALTAVILLA*
Affiliation:
Dipartimento di Ingegneria Industriale e Scienze Matematiche, Università Politecnica delle Marche, Via Brecce Bianche, 60131, Ancona, Italy email [email protected]
E. BALLICO
Affiliation:
Dipartimento Di Matematica, Università di Trento, Via Sommarive 14, 38123, Povo, Trento, Italy email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that a reduced and irreducible algebraic surface in 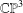$\mathbb{CP}^{3}$ containing infinitely many twistor lines cannot have odd degree. Then, exploiting the theory of quaternionic slice regularity and the normalisation map of a surface, we give constructive existence results for even degrees.

Keywords

twistor fibrationlines on surfacesrational and ruled surfacesPlücker quadricslice regularity

MSC classification

Primary: 14D21: Applications of vector bundles and moduli spaces in mathematical physics (twistor theory, instantons, quantum field theory)
Secondary: 14J26: Rational and ruled surfaces 32L25: Twistor theory, double fibrations 30G35: Functions of hypercomplex variables and generalized variables 53C28: Twistor methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 61 - 70
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Both authors are members of GNSAGA of INdAM; the first author was supported by SIR grants, Nos. RBSI14CFME and RBSI14DYEB, and an INdAM fellowship and thanks the Clifford Research Group at Ghent University where this fellowship was spent; the second author was supported by a grant from MIUR PRIN 2015.

References

Altavilla, A., ‘Twistor interpretation of slice regular functions’, J. Geom. Phys. 123 (2018), 184–208.Google Scholar
Altavilla, A. and Ballico, E., ‘Twistor lines on algebraic surfaces’, Ann. Glob. Anal. Geom. 55(3) (2019), 555–573.Google Scholar
Altavilla, A. and Ballico, E., ‘Three topological results on the twistor discriminant locus in the 4-sphere’, Milan J. Math. 87(1) (2019), 57–72.Google Scholar
Altavilla, A. and Sarfatti, G., ‘Slice-polynomial functions and twistor geometry of ruled surfaces in ℂℙ3 ’, Math. Z. 291(3–4) (2019), 1059–1092.Google Scholar
Armstrong, J., ‘The twistor discriminant locus of the Fermat cubic’, New York J. Math. 21 (2015), 485–510.Google Scholar
Armstrong, J., Povero, M. and Salamon, S., ‘Twistor lines on cubic surfaces’, Rend. Semin. Mat. Univ. Politec. Torino 71(3–4) (2013), 317–338.Google Scholar
Armstrong, J. and Salamon, S., ‘Twistor topology of the Fermat cubic’, SIGMA Symmetry Integrability Geom. Methods Appl. 10 (2014), Article ID 061, 12 pages.Google Scholar
Ballico, E., ‘Conformal automorphisms of algebraic surfaces and algebraic curves in the complex projective space’, J. Geom. Phys. 134 (2018), 153–160.Google Scholar
Chirka, E. M., ‘Orthogonal complex structures in ℝ4 ’, Russ. Math. Surv. 73 (2018), 91–159.Google Scholar
Gentili, G., Salamon, S. and Stoppato, C., ‘Twistor transforms of quaternionic functions and orthogonal complex structures’, J. Eur. Math. Soc. (JEMS) 16(11) (2014), 2323–2353.Google Scholar
Gentili, G., Stoppato, C. and Struppa, D. C., Regular Functions of a Quaternionic Variable, Springer Monographs in Mathematics (Springer, Heidelberg, 2013).Google Scholar
Gross, B. and Harris, J., ‘Real algebraic curves’, Ann. Sci. Éc. Norm. Supér. (4) 14(2) (1981), 157–182.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, 52 (Springer, New York–Heidelberg, 1977).Google Scholar
Lange, H. and Narasimhan, M. S., ‘Maximal subbundles of rank two vector bundles on curves’, Math. Ann. 266(1) (1983), 55–72.Google Scholar
LeBrun, C., ‘Anti-self-dual metrics and Kähler geometry’, in: Proceedings of the International Congress of Mathematicians (Zürich, 1994) (ed. Chatterji, S. D.) (Birkhäuser, Basel, 1995), 498–507.Google Scholar
Salamon, S. and Viaclovsky, J., ‘Orthogonal complex structures on domains in ℝ4 ’, Math. Ann. 343(4) (2009), 853–899.Google Scholar
Seppälä, M., ‘Moduli spaces of stable real algebraic curves’, Ann. Sci. Éc. Norm. Supér. (4) 24(5) (1991), 519–544.Google Scholar