Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-21T18:32:24.876Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME COUNTING FORMULAE FOR 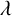$\lambda $-QUIDDITIES OVER THE RINGS 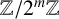${\mathbb {Z}}/2^{m}{\mathbb {Z}}$

Part of: Combinatorics

Published online by Cambridge University Press:  16 May 2024

FLAVIEN MABILAT Open the ORCID record for FLAVIEN MABILAT [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

The 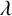$\lambda $-quiddities of size n are n-tuples of elements of a fixed set, solutions of a matrix equation appearing in the study of Coxeter’s friezes. Their number and properties are closely linked to the structure and the cardinality of the chosen set. Our main objective is an explicit formula giving the number of 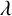$\lambda $-quiddities of odd size, and a lower and upper bound for the number of 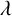$\lambda $-quiddities of even size, over the rings 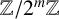${\mathbb {Z}}/2^{m}{\mathbb {Z}}$ (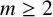$m \geq 2$). We also give explicit formulae for the number of 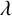$\lambda $-quiddities of size n over 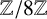${\mathbb {Z}}/8{\mathbb {Z}}$.

Keywords

λ-quidditymodular grouprings ℤ/2mℤCoxeter’s friezes

MSC classification

Primary: 05A15: Exact enumeration problems, generating functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Conley, C. and Ovsienko, V., ‘Quiddities of polygon dissections and the Conway–Coxeter frieze equation’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 24(4) (2023), 2125–2170.Google Scholar
Coxeter, H. S. M., ‘Frieze patterns’, Acta Arith. 18 (1971), 297–310.CrossRefGoogle Scholar
Cuntz, M. and Holm, T., ‘Frieze patterns over integers and other subsets of the complex numbers’, J. Comb. Algebra 3(2) (2019), 153–188.CrossRefGoogle Scholar
Cuntz, M. and Mabilat, F., ‘Comptage des quiddités sur les corps finis et sur quelques anneaux $\mathbb{Z}/N\mathbb{Z}$ ’, Ann. Fac. Sci. Toulouse Math. (6), to appear, arXiv:2304.03071.Google Scholar
Mabilat, F., ‘Combinatoire des sous-groupes de congruence du groupe modulaire’, Ann. Math. Blaise Pascal 28(1) (2021), 7–43.CrossRefGoogle Scholar
Mabilat, F., ‘ $\lambda$ -quiddité sur $\mathbb{Z}[\alpha ]$ avec $\alpha$ transcendant’, Math. Scand. 128(1) (2022), 5–13.CrossRefGoogle Scholar
Mabilat, F., ‘Solutions monomiales minimales irréductibles dans ${SL}_2(\mathbb{Z}/{p}^n\mathbb{Z})$ ’, Bull. Sci. Math., to appear, arXiv:2202.07279.Google Scholar
Morier-Genoud, S., ‘Coxeter’s frieze patterns at the crossroad of algebra, geometry and combinatorics’, Bull. Lond. Math. Soc. 47(6) (2015), 895–938.CrossRefGoogle Scholar
Morier-Genoud, S., ‘Counting Coxeter’s friezes over a finite field via moduli spaces’, Algebr. Comb. 4(2) (2021), 225–240.Google Scholar
Ovsienko, V., ‘Partitions of unity in $\mathrm{SL}(2,\mathbb{Z})$ , negative continued fractions, and dissections of polygons’, Res. Math. Sci. 5(2) (2018), Article no. 21.CrossRefGoogle Scholar
Short, I., Van Son, M. and Zabolotskii, A., ‘Frieze patterns and Farey complexes’, Preprint, 2023, arXiv:2312.12953.Google Scholar