Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-22T19:35:22.526Z Has data issue: false hasContentIssue false
  • English
  • Français

A REIDEMEISTER THEOREM FOR SOLID RIBBON TORUS LINKS

Published online by Cambridge University Press:  22 October 2024

ZSUZSANNA DANCSO Open the ORCID record for ZSUZSANNA DANCSO [Opens in a new window]  and
THOMAS MALLIARAS GAVRIELATOS Open the ORCID record for THOMAS MALLIARAS GAVRIELATOS [Opens in a new window]
ZSUZSANNA DANCSO*
Affiliation:
School of Mathematics and Statistics, The University of Sydney, Sydney, New South Wales, 2006, Australia
THOMAS MALLIARAS GAVRIELATOS
Affiliation:
School of Mathematics and Statistics, The University of Sydney, Sydney, New South Wales, 2006, Australia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A complete Reidemeister characterisation of welded links is a long-standing open problem. We present a Reidemeister theorem for a related class of four-dimensional links: solid ribbon torus links, that is, immersed solid tori in 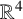$\mathbb {R}^4$ with only ribbon singularities, considered up to generalised ribbon isotopy.

Keywords

Reidemeister theoremribbon torus linkstube mapwelded links
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 15
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alexander, J. W., ‘On the deformation of an $n$ -cell’, Proc. Natl. Acad. Sci. USA 9 (1923), 406–407.CrossRefGoogle ScholarPubMed
Audoux, B., ‘On the welded tube map’, Contemp. Math. 670 (2016), 261–284.CrossRefGoogle Scholar
Audoux, B., Applications de modèles combinatoires issus de la topologie: Classification des enlacements d’anneaux à homotopie d’enlacement près & Produits et puissances itérés de codes quantiques CSS, Aix-Marseille Université Mémoire d’Habilitation à Diriger des Recherches (2018).Google Scholar
Audoux, B., Bellingeri, P., Meilhan, J.-B. and Wagner, E., ‘Homotopy classification of ribbon tubes and welded string links,’ Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 17 (2017), 713–761.Google Scholar
Audoux, B., Bellingeri, P., Meilhan, J.-B. and Wagner, E., ‘On usual, virtual and welded knotted objects’, J. Math. Soc. Japan 69(3) (2017), 1079–1097.CrossRefGoogle Scholar
Audoux, B. and Meilhan, J.-B., ‘Characterization of the reduced peripheral system of links’, J. Inst. Math. Jussieu, to appear. Published online (1 February 2024), 19 pages.CrossRefGoogle Scholar
Bar-Natan, D. and Dancso, Z., ‘Finite type invariants of w-knotted objects I: w-knots and the Alexander polynomial’, Algebr. Geom. Topol. 16 (2016), 1063–1133.CrossRefGoogle Scholar
Brendle, T. and Hatcher, A., ‘Configuration spaces of rings and wickets’, Comment. Math. Helv. 88(1) (2013), 131–162.CrossRefGoogle Scholar
Fenn, R., Rimányi, R. and Rourke, C., ‘The braid-permutation group’, Topology 36(1) (1997), 123–135.CrossRefGoogle Scholar
Goldsmith, D. L., ‘The theory of motion groups’, Michigan Math. J. 28(1) (1981), 3–17.CrossRefGoogle Scholar
Satoh, S., ‘Virtual knot presentation of ribbon torus-knots’, J. Knot Theory Ramifications 9(4) (2000), 531–542.CrossRefGoogle Scholar
Winter, B., ‘The classification of spun torus knots,’ J. Knot Theory Ramifications 18(9) (2009), 1287–1298.CrossRefGoogle Scholar
Yajima, T., ‘On the fundamental groups of knotted 2-manifolds in the 4-space’, Osaka J. Math. 13 (1962), 63–71.Google Scholar
Yanagawa, T., ‘On ribbon 2-knots: the 3-manifold bounded by the 2-knots’, Osaka J. Math. 6 (1969), 447–464.Google Scholar
Yanagawa, T., ‘On ribbon 2-knots II: the second homotopy group of the complementary domain’, Osaka J. Math. 6 (1969), 465–473.Google Scholar
Yanagawa, T., ‘On ribbon 2-knots III: on the unknotting of ribbon 2-knots in ${S}^4$ ’, Osaka J. Math. 7 (1970), 165–172.Google Scholar