Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-25T15:32:32.975Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASICONFORMAL HARMONIC MAPPINGS BETWEEN DOMAINS CONTAINING INFINITY

Part of: Two-dimensional theory Geometric function theory

Published online by Cambridge University Press:  08 January 2020

DAVID KALAJ
DAVID KALAJ*
Affiliation:
Faculty of Natural Sciences and Mathematics,University of Montenegro, Cetinjski put b.b. 81000Podgorica, Montenegro email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Assume that $\unicode[STIX]{x1D6FA}$ and 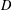$D$ are two domains with compact smooth boundaries in the extended complex plane 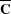$\overline{\mathbf{C}}$. We prove that every quasiconformal mapping between $\unicode[STIX]{x1D6FA}$ and 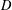$D$ mapping $\infty$ onto itself is bi-Lipschitz continuous with respect to both the Euclidean and Riemannian metrics.

Keywords

quasiconformal mappingscomplement of the unit diskquasi-isometry

MSC classification

Primary: 31A05: Harmonic, subharmonic, superharmonic functions
Secondary: 30C62: Quasiconformal mappings in the plane
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 109 - 117
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Astala, K. and Manojlović, V., ‘On Pavlović theorem in space’, Potential Anal. 43(3) (2015), 361–370.CrossRefGoogle Scholar
Božin, V. and Mateljević, M., ‘Quasiconformal and HQC mappings between Lyapunov Jordan domains’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), to appear, 23 pages, doi: 10.2422/20362145.201708_013.Google Scholar
Duren, P., Harmonic Mappings in the Plane, Cambridge Tracts in Mathematics, 156 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Goluzin, G. M., Geometric Function Theory of a Complex Variable, Translations of Mathematical Monographs, 26 (American Mathematical Society, Providence, RI, 1969).10.1090/mmono/026CrossRefGoogle Scholar
Heinz, E., ‘On one-to-one harmonic mappings’, Pacific J. Math. 9 (1959), 101–105.10.2140/pjm.1959.9.101CrossRefGoogle Scholar
Hengartner, W. and Schober, G., ‘Harmonic mappings with given dilatation’, J. Lond. Math. Soc. Ser. II 33 (1986), 473–483.10.1112/jlms/s2-33.3.473CrossRefGoogle Scholar
Hengartner, W. and Schober, G., ‘Univalent harmonic functions’, Trans. Amer. Math. Soc. 299 (1987), 1–31.10.1090/S0002-9947-1987-0869396-9CrossRefGoogle Scholar
Kalaj, D., ‘Quasiconformal harmonic mapping between Jordan domains’, Math. Z. 260(2) (2008), 237–252.CrossRefGoogle Scholar
Kalaj, D., ‘Harmonic maps between annuli on Riemann surfaces’, Israel J. Math. 182 (2011), 123–147.CrossRefGoogle Scholar
Kalaj, D., ‘Harmonic mappings and distance function’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 10(3) (2011), 669–681.Google Scholar
Kalaj, D., ‘Quasiconformal harmonic mappings between Dini’s smooth Jordan domains’, Pacific J. Math. 276 (2015), 213–228.CrossRefGoogle Scholar
Kalaj, D. and Pavlović, M., ‘Boundary correspondence under quasiconformal harmonic diffeomorphisms of a half-plane’, Ann. Acad. Sci. Fenn. Math. 30(1) (2005), 159–165.Google Scholar
Kalaj, D. and Saksman, E., ‘Quasiconformal maps with controlled Laplacian’, J. Anal. Math. 137(1) (2019), 251–268.CrossRefGoogle Scholar
Kalaj, D. and Zlatičanin, A., ‘Quasiconformal mappings with controlled Laplacian and Hölder continuity’, Ann. Acad. Sci. Fenn. Math. 44(2) (2019), 797–803.CrossRefGoogle Scholar
Lesley, F. D. and Warschawski, S. E., ‘On conformal mappings with derivative in VMOA’, Math. Z. 158 (1978), 275–283.CrossRefGoogle Scholar
Manojlović, V., ‘Bi-Lipschicity of quasiconformal harmonic mappings in the plane’, Filomat 23(1) (2009), 85–89.CrossRefGoogle Scholar
Martio, O., ‘On harmonic quasiconformal mappings’, Ann. Acad. Sci. Fenn. Ser. A I 425 (1986), 10 pages.Google Scholar
Partyka, D., Sakan, K.-I. and Zhu, J.-F., ‘Quasiconformal harmonic mappings with the convex holomorphic part’, Ann. Acad. Sci. Fenn. Math. 43(1) (2018), 401–418; erratum, Ann. Acad. Sci. Fenn. Math. 43(2) (2018), 1085–1086.CrossRefGoogle Scholar
Pavlović, M., ‘Boundary correspondence under harmonic quasiconformal homeomorphisms of the unit disc’, Ann. Acad. Sci. Fenn. Math. 27 (2002), 365–372.Google Scholar
Pavlović, M., Introduction to Function Spaces on the Disk (Matematički Institut SANU, Belgrade, 2004).Google Scholar
Zygmund, A., Trigonometric Series I (Cambrige University Press, Cambridge, 1958).Google Scholar