Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T08:08:34.304Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD

Part of: General field theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  25 April 2022

ANDREW R. BOOKER Open the ORCID record for ANDREW R. BOOKER [Opens in a new window] ,
STEPHEN D. COHEN Open the ORCID record for STEPHEN D. COHEN [Opens in a new window] ,
NICOL LEONG Open the ORCID record for NICOL LEONG [Opens in a new window]  and
TIM TRUDGIAN Open the ORCID record for TIM TRUDGIAN [Opens in a new window]
ANDREW R. BOOKER
Affiliation:
School of Mathematics, University of Bristol, Bristol BS8 1UG, UK e-mail: [email protected]
STEPHEN D. COHEN
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow G12 8QQ, UK e-mail: [email protected]
NICOL LEONG
Affiliation:
School of Science, The University of New South Wales Canberra, Canberra ACT 2610, Australia e-mail: [email protected]
TIM TRUDGIAN*
Affiliation:
School of Science, The University of New South Wales Canberra, Canberra ACT 2610, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

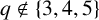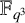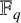We prove that for any prime power $q\notin \{3,4,5\}$ , the cubic extension $\mathbb {F}_{q^{3}}$ of the finite field $\mathbb {F}_{q}$ contains a primitive element 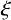$\xi $ such that 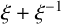$\xi +\xi ^{-1}$ is also primitive, and 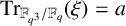$\operatorname {\mathrm {Tr}}_{\mathbb {F}_{q^{3}}/\mathbb {F}_{q}}(\xi )=a$ for any prescribed 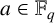$a\in \mathbb {F}_{q}$ . This completes the proof of a conjecture of Gupta et al. [‘Primitive element pairs with one prescribed trace over a finite field’, Finite Fields Appl. 54 (2018), 1–14] concerning the analogous problem over an extension of arbitrary degree 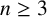$n\ge 3$ .

Keywords

finite fieldfield extensionprimitive elementprime sieve algorithm

MSC classification

Primary: 12E20: Finite fields (field-theoretic aspects)
Secondary: 11T23: Exponential sums
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 458 - 462
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

T. Trudgian was supported by Australian Research Council Future Fellowship FT160100094.

References

Booker, A. R., Cohen, S. D., Leong, N. and Trudgian, T., ‘Primitive elements with prescribed traces’, Preprint, 2022, arXiv:2112.10268.CrossRefGoogle Scholar
Cohen, S. D. and Gupta, A., ‘Primitive element pairs with a prescribed trace in the quartic extension of a finite field’, J. Algebra Appl. 20(6) (2021), Article no. 2150168.CrossRefGoogle Scholar
de Rooij, P., ‘Efficient exponentiation using precomputation and vector addition chains’, in: Advances in Cryptology—EUROCRYPT’94 (Perugia) (ed. A. De Santis), Lecture Notes in Computer Science, 950 (Springer, Berlin, 1995), 389–399.CrossRefGoogle Scholar
Gupta, A., Sharma, R. K. and Cohen, S. D., ‘Primitive element pairs with one prescribed trace over a finite field’, Finite Fields Appl. 54 (2018), 1–14.CrossRefGoogle Scholar
Sutherland, A. V., ff_poly, version 1.2.7, 2015, available from https://math.mit.edu/~drew/ff_ poly_v1.2.7.tar.Google Scholar
The PARI Group, PARI/GP version 2.13.3, Univ. Bordeaux, 2021, available from http://pari.math.u- bordeaux.fr/.Google Scholar