Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T16:17:46.900Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CONNECTION BETWEEN DIFFERENTIAL POLYNOMIAL RINGS AND POLYNOMIAL RINGS OVER NIL RINGS

Part of: Radicals and radical properties of rings

Published online by Cambridge University Press:  16 September 2019

LOUISA CATALANO Open the ORCID record for LOUISA CATALANO [Opens in a new window]  and
MEGAN CHANG-LEE Open the ORCID record for MEGAN CHANG-LEE [Opens in a new window]
LOUISA CATALANO*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email [email protected]
MEGAN CHANG-LEE
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, CA 94720, USA email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study some connections between the polynomial ring 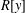$R[y]$ and the differential polynomial ring 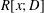$R[x;D]$. In particular, we answer a question posed by Smoktunowicz, which asks whether 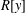$R[y]$ is nil when 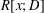$R[x;D]$ is nil, provided that 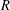$R$ is an algebra over a field of positive characteristic and 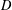$D$ is a locally nilpotent derivation.

Keywords

nil ringdifferential polynomial ringlocally nilpotent ring

MSC classification

Primary: 16N40: Nil and nilpotent radicals, sets, ideals, rings
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 3 , June 2020 , pp. 438 - 441
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are supported in part by NSF grant DMS 1653002.

References

Amitsur, S. A., ‘Radicals of polynomial rings’, Canad. J. Math. 8 (1956), 355–361.10.4153/CJM-1956-040-9Google Scholar
Smoktunowicz, A., ‘Polynomial rings over nil rings need not be nil’, J. Algebra 233 (2000), 427–436.Google Scholar
Smoktunowicz, A., ‘How far can we go with Amitsur’s theorem in differential polynomial rings?’, Israel J. Math. 219 (2017), 555–608.10.1007/s11856-017-1491-1Google Scholar
Smoktunowicz, A. and Ziembowski, M., ‘Differential polynomial rings over locally nilpotent rings need not be Jacobson radical’, J. Algebra 412 (2014), 207–217.Google Scholar