Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-20T10:27:40.594Z Has data issue: false hasContentIssue false
  • English
  • Français

ON 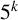$5^k$-REGULAR PARTITIONS MODULO POWERS OF 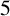$5$

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  14 April 2025

B. HEMANTHKUMAR Open the ORCID record for B. HEMANTHKUMAR [Opens in a new window]  and
D. S. GIREESH Open the ORCID record for D. S. GIREESH [Opens in a new window]
B. HEMANTHKUMAR
Affiliation:
Department of Mathematics, RV College of Engineering, RV Vidyanikethan Post, Mysore Road, Bengaluru 560 059, Karnataka, India e-mail: [email protected]
D. S. GIREESH*
Affiliation:
Department of Mathematics, BMS College of Engineering, P.O. Box No. 1908, Bull Temple Road, Bengaluru 560 019, Karnataka, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we investigate the arithmetic properties of 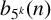$b_{5^k}(n)$, which counts the partitions of n where no part is divisible by 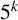$5^k$. By constructing generating functions for 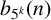$b_{5^k}(n)$ across specific arithmetic progressions, we establish a set of Ramanujan-type congruences.

Keywords

partitionsℓ-regular partitionsgenerating functionscongruences

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A15: Exact enumeration problems, generating functions 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Hirschhorn, M. D. and Hunt, D. C., ‘A simple proof of the Ramanujan conjecture for powers of 5’, J. reine angew. Math. 326 (1981), 1–17.Google Scholar
Ramanujan, S., Collected Papers of Srinivasa Ramanujan (eds. Hardy, G. H., Seshu Aiyar, P. V. and Wilson, B. M.) (AMS Chelsea Publishing, Providence, RI, 2000).Google Scholar
Ranganatha, D., ‘Ramanujan-type congruences modulo powers of 5 and 7’, Indian J. Pure Appl. Math. 48 (2017), 449–465.CrossRefGoogle Scholar
Wang, L., ‘Congruences for $5$ -regular partitions modulo powers of $5$ ’, Ramanujan J. 44 (2017), 343–358.Google Scholar
Watson, G. N., ‘Ramanujans Vermutung über Zerfällungsanzahlen’, J. reine angew. Math. 179 (1938), 97–128.CrossRefGoogle Scholar