Article contents
A NOTE ON SPIRALLIKE FUNCTIONS
Published online by Cambridge University Press: 25 March 2021
Abstract
Let f be analytic in the unit disk
 $\mathbb {D}=\{z\in \mathbb {C}:|z|<1 \}$
and let
$\mathbb {D}=\{z\in \mathbb {C}:|z|<1 \}$
and let
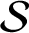 ${\mathcal S}$
be the subclass of normalised univalent functions with
${\mathcal S}$
be the subclass of normalised univalent functions with
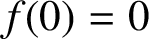 $f(0)=0$
and
$f(0)=0$
and
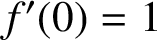 $f'(0)=1$
, given by
$f'(0)=1$
, given by
 $f(z)=z+\sum _{n=2}^{\infty }a_n z^n$
. Let F be the inverse function of f, given by
$f(z)=z+\sum _{n=2}^{\infty }a_n z^n$
. Let F be the inverse function of f, given by
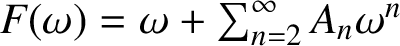 $F(\omega )=\omega +\sum _{n=2}^{\infty }A_n \omega ^n$
for
$F(\omega )=\omega +\sum _{n=2}^{\infty }A_n \omega ^n$
for
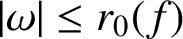 $|\omega |\le r_0(f)$
. Denote by
$|\omega |\le r_0(f)$
. Denote by
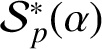 $ \mathcal {S}_p^{* }(\alpha )$
the subset of
$ \mathcal {S}_p^{* }(\alpha )$
the subset of
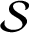 $ \mathcal {S}$
consisting of the spirallike functions of order
$ \mathcal {S}$
consisting of the spirallike functions of order
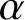 $\alpha $
in
$\alpha $
in
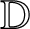 $\mathbb {D}$
, that is, functions satisfying
$\mathbb {D}$
, that is, functions satisfying
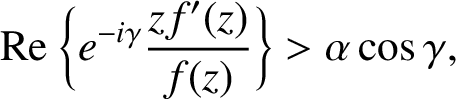
for
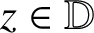 $z\in \mathbb {D}$
,
$z\in \mathbb {D}$
,
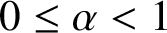 $0\le \alpha <1$
and
$0\le \alpha <1$
and
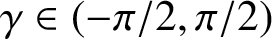 $\gamma \in (-\pi /2,\pi /2)$
. We give sharp upper and lower bounds for both
$\gamma \in (-\pi /2,\pi /2)$
. We give sharp upper and lower bounds for both
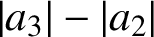 $ |a_3|-|a_2| $
and
$ |a_3|-|a_2| $
and
 $ |A_3|-|A_2| $
when
$ |A_3|-|A_2| $
when
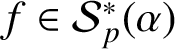 $f\in \mathcal {S}_p^{* }(\alpha )$
, thus solving an open problem and presenting some new inequalities for coefficient differences.
$f\in \mathcal {S}_p^{* }(\alpha )$
, thus solving an open problem and presenting some new inequalities for coefficient differences.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 117 - 123
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
- 4
- Cited by



