ISOMORPHISM OF RELATIVE HOLOMORPHS AND MATRIX SIMILARITY

Abstract

Let V be a finite dimensional vector space over the field with p elements, where p is a prime number. Given arbitrary 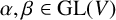$\alpha ,\beta \in \mathrm {GL}(V)$, we consider the semidirect products 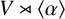$V\rtimes \langle \alpha \rangle $ and 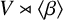$V\rtimes \langle \beta \rangle $, and show that if 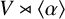$V\rtimes \langle \alpha \rangle $ and $V\rtimes \langle \beta \rangle $ are isomorphic, then 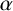$\alpha $ must be similar to a power of $\beta $ that generates the same subgroup as 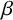$\beta $; that is, if H and K are cyclic subgroups of $\mathrm {GL}(V)$ such that 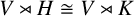$V\rtimes H\cong V\rtimes K$, then H and K must be conjugate subgroups of 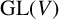$\mathrm {GL}(V)$. If we remove the cyclic condition, there exist examples of nonisomorphic, let alone nonconjugate, subgroups H and K of 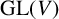$\mathrm {GL}(V)$ such that 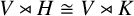$V\rtimes H\cong V\rtimes K$. Even if we require that noncyclic subgroups H and K of 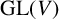$\mathrm {GL}(V)$ be abelian, we may still have 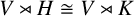$V\rtimes H\cong V\rtimes K$ with H and K nonconjugate in 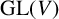$\mathrm {GL}(V)$, but in this case, H and K must at least be isomorphic. If we replace V by a free module U over 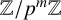${\mathbb {Z}}/p^m{\mathbb {Z}}$ of finite rank, with 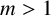$m>1$, it may happen that 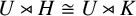$U\rtimes H\cong U\rtimes K$ for nonconjugate cyclic subgroups of 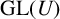$\mathrm {GL}(U)$. If we completely abandon our requirements on V, a sufficient criterion is given for a finite group G to admit nonconjugate cyclic subgroups H and K of 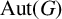$\mathrm {Aut}(G)$ such that 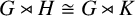$G\rtimes H\cong G\rtimes K$. This criterion is satisfied by many groups.