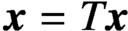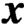Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abramov, Vyacheslav M.
2024.
Fixed-point theorem for an infinite Toeplitz matrix and its extension to general infinite matrices.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 76,
Issue. 3,
Abramov, Vyacheslav M.
2024.
Fixed-Point Theorem for an Infinite Toeplitz Matrix and Its Extension to General Infinite Matrices.
Ukrainian Mathematical Journal,
Vol. 76,
Issue. 3,
p.
349.