Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-20T16:11:54.292Z Has data issue: false hasContentIssue false
  • English
  • Français

EVERY ARITHMETIC PROGRESSION CONTAINS INFINITELY MANY b-NIVEN NUMBERS

Part of: Sequences and sets Elementary number theory

Published online by Cambridge University Press:  31 July 2023

JOSHUA HARRINGTON Open the ORCID record for JOSHUA HARRINGTON [Opens in a new window] ,
MATTHEW LITMAN Open the ORCID record for MATTHEW LITMAN [Opens in a new window]  and
TONY W. H. WONG Open the ORCID record for TONY W. H. WONG [Opens in a new window]
JOSHUA HARRINGTON
Affiliation:
Department of Mathematics, Cedar Crest College, 100 College Dr, Allentown, PA 18104, USA e-mail: [email protected]
MATTHEW LITMAN
Affiliation:
Department of Mathematics, University of California, Davis, 1 Shields Ave, Davis, CA 95616, USA e-mail: [email protected]
TONY W. H. WONG*
Affiliation:
Department of Mathematics, Kutztown University of Pennsylvania, 15200 Kutztown Rd, Kutztown, PA 19530, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For an integer 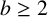$b\geq 2$, a positive integer is called a b-Niven number if it is a multiple of the sum of the digits in its base-b representation. In this article, we show that every arithmetic progression contains infinitely many b-Niven numbers.

Keywords

Niven numberarithmetic progression

MSC classification

Primary: 11A63: Radix representation; digital problems
Secondary: 11B25: Arithmetic progressions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 409 - 413
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Cooper, C. and Kennedy, R. E., ‘On consecutive Niven numbers’, Fibonacci Quart. 31 (1993), 146–151.CrossRefGoogle Scholar
De Koninck, J.-M., Doyon, N. and Kátai, I., ‘On the counting function for the Niven numbers’, Acta Arith. 106 (2003), 265–275.CrossRefGoogle Scholar
De Koninck, J.-M., Doyon, N. and Kátai, I., ‘Counting the number of twin Niven numbers’, Ramanujan J. 17 (2008), 89–105.CrossRefGoogle Scholar
Grundman, H., ‘Sequences of consecutive $n$ -Niven numbers’, Fibonacci Quart. 32 (1994), 174–175.CrossRefGoogle Scholar
Grundman, H., Harrington, J. and Wong, T. W. H., ‘Arithmetic progressions of $b$ -Niven numbers’, Rocky Mountain J. Math., to appear.Google Scholar
Wilson, B., ‘Construction of $2\ast n$ consecutive $n$ -Niven numbers’, Fibonacci Quart. 35 (1997), 122–128.Google Scholar