Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-20T10:49:34.420Z Has data issue: false hasContentIssue false
  • English
  • Français

EDGE WEIGHTING FUNCTIONS ON THE SEMITOTAL DOMINATING SET OF CLAW-FREE GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  12 February 2024

JIE CHEN Open the ORCID record for JIE CHEN [Opens in a new window] ,
HONGZHANG CHEN Open the ORCID record for HONGZHANG CHEN [Opens in a new window]  and
SHOU-JUN XU Open the ORCID record for SHOU-JUN XU [Opens in a new window]
JIE CHEN
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China e-mail: [email protected]
HONGZHANG CHEN
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China e-mail: [email protected]
SHOU-JUN XU*
Affiliation:
School of Mathematics and Statistics, Gansu Center for Applied Mathematics, Lanzhou University, Lanzhou, Gansu 730000, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by 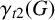$\gamma _{t2}(G)$, is the minimum cardinality of a semitotal dominating set in G. Using edge weighting functions on semitotal dominating sets, we prove that if 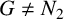$G\neq N_2$ is a connected claw-free graph of order 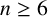$n\geq 6$ with minimum degree 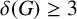$\delta (G)\geq 3$, then 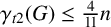$\gamma _{t2}(G)\leq \frac{4}{11}n$ and this bound is sharp, disproving the conjecture proposed by Zhu et al. [‘Semitotal domination in claw-free cubic graphs’, Graphs Combin. 33(5) (2017), 1119–1130].

Keywords

claw-free graphedge weighting functionsemitotal domination

MSC classification

Primary: 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 177 - 188
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was funded in part by the National Natural Science Foundation of China (Grant No. 12071194) and the Chongqing Natural Science Foundation Innovation and Development Joint Fund (Municipal Education Commission) (Grant No. CSTB2022NSCQ-LZX0003).

References

Chen, J. and Xu, S.-J., ‘A characterization of 3- $\gamma$ -critical graphs which are not bicritical’, Inform. Process. Lett. 166 (2021), Article no. 106062.10.1016/j.ipl.2020.106062CrossRefGoogle Scholar
Dong, Y. X., Shan, E. F., Kang, L. Y. and Li, S., ‘Domination in intersecting hypergraphs’, Discrete Appl. Math. 251 (2018), 155–159.10.1016/j.dam.2018.05.039CrossRefGoogle Scholar
Goddard, W., Henning, M. A. and McPillan, C. A., ‘Semitotal domination in graphs’, Util. Math. 94 (2014), 67–81.Google Scholar
Haynes, T. W., Hedetniemi, S. T. and Slater, P. J., Fundamentals of Domination in Graphs (Marcel Dekker Inc., New York, 1998).Google Scholar
Henning, M. A., ‘Edge weighting functions on semitotal dominating sets’, Graphs Combin. 33 (2017), 403–417.10.1007/s00373-017-1769-4CrossRefGoogle Scholar
Henning, M. A., ‘Bounds on domination parameters in graphs: a brief survey’, Discuss. Math. Graph Theory 42 (2022), 665–708.10.7151/dmgt.2454CrossRefGoogle Scholar
Henning, M. A., Kang, L., Shan, E. and Yeo, A., ‘On matching and total domination in graphs’, Discrete Math. 308 (2008), 2313–2318.10.1016/j.disc.2006.10.024CrossRefGoogle Scholar
Henning, M. A. and Marcon, A. J., ‘On matching and semitotal domination in graphs’, Discrete Math. 324 (2014), 13–18.10.1016/j.disc.2014.01.021CrossRefGoogle Scholar
Henning, M. A. and Marcon, A. J., ‘Semitotal domination in claw-free cubic graphs’, Ann. Comb. 20(4) (2016), 1–15.10.1007/s00026-016-0331-zCrossRefGoogle Scholar
Henning, M. A. and Pandey, A., ‘Algorithmic aspects of semitotal domination in graphs’, Theoret. Comput. Sci. 766 (2019), 46–57.10.1016/j.tcs.2018.09.019CrossRefGoogle Scholar
Henning, M. A. and Yeo, A., Total Domination in Graphs (Springer, New York, 2013).10.1007/978-1-4614-6525-6CrossRefGoogle Scholar
Zhu, E. and Liu, C., ‘On the semitotal domination number of line graphs’, Discrete Appl. Math. 254 (2019), 295–298.10.1016/j.dam.2018.06.010CrossRefGoogle Scholar
Zhu, E., Shao, Z. and Xu, J., ‘Semitotal domination in claw-free cubic graphs’, Graphs Combin. 33(5) (2017), 1119–1130.10.1007/s00373-017-1826-zCrossRefGoogle Scholar