No CrossRef data available.
Article contents
DISCREPANCY BOUNDS FOR THE DISTRIBUTION OF RANKIN–SELBERG L-FUNCTIONS
Part of:
Probabilistic theory: distribution modulo $1$; metric theory of algorithms
Discontinuous groups and automorphic forms
Published online by Cambridge University Press: 18 October 2024
Abstract
We investigate the discrepancy between the distributions of the random variable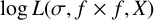 
$\log L (\sigma , f \times f, X)$ and that of 
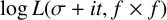$\log L(\sigma +it, f \times f)$, that is, 
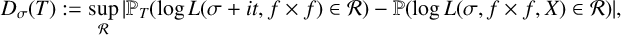$$ \begin{align*} D_{\sigma} (T) := \sup_{\mathcal{R}} |\mathbb{P}_T(\log L(\sigma+it, f \times f) \in \mathcal{R}) - \mathbb{P}(\log L(\sigma, f \times f, X) \in \mathcal{R})|, \end{align*} $$
where the supremum is taken over rectangles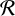 
$\mathcal {R}$ with sides parallel to the coordinate axes. For fixed 
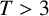$T>3$ and 
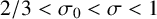$2/3 <\sigma _0 < \sigma < 1$, we prove that 
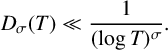$$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}. \end{align*} $$
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 32 - 42
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is supported by The Science and Technology Development Fund, Macau SAR (File no. 0084/2022/A).
References
Bohr, H. and Jessen, B., ‘Über die Werteverteilung der Riemannschen Zetafunktion’, Acta Math. 54 (1930), 1–35.CrossRefGoogle Scholar
Deligne, P., ‘La conjecture de Weil. I’, Publ. Math. Inst. Hautes Études Sci. 43 (1974), 273–307.CrossRefGoogle Scholar
Dong, Z., Wang, W. and Zhang, H., ‘Distribution of Dirichlet
$L$
-functions’, Mathematika 69 (2023), 719–750.CrossRefGoogle Scholar
$L$
-functions’, Mathematika 69 (2023), 719–750.CrossRefGoogle ScholarHarman, G. and Matsumoto, K., ‘Discrepancy estimates for the value-distribution of the Riemann zeta-function, IV’, J. Lond. Math. Soc. (2) 50 (1994), 17–24.CrossRefGoogle Scholar
Huang, J., Zhai, W. and Zhang, D., ‘Higher power moments of symmetric square
$L$
-function’, J. Number Theory 243 (2023), 495–517.CrossRefGoogle Scholar
$L$
-function’, J. Number Theory 243 (2023), 495–517.CrossRefGoogle ScholarIwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2021).Google Scholar
Lamzouri, Y., ‘Distribution of values of
$L$
-functions at the edge of the critical strip’, Proc. Lond. Math. Soc. (3) 100 (2010), 835–863.CrossRefGoogle Scholar
$L$
-functions at the edge of the critical strip’, Proc. Lond. Math. Soc. (3) 100 (2010), 835–863.CrossRefGoogle ScholarLamzouri, Y., Lester, S. and Radziwiłł, M., ‘Discrepancy bounds for the distribution of the Riemann zeta-function and applications’, J. Anal. Math. 139 (2019), 453–494.CrossRefGoogle Scholar
Lee, Y., ‘Discrepancy bounds for the distribution of
$L$
-functions near the critical line’, Preprint, 2023, arXiv:2304.03415.Google Scholar
$L$
-functions near the critical line’, Preprint, 2023, arXiv:2304.03415.Google ScholarLü, G., ‘Shifted convolution sums of Fourier coefficients with divisor functions’, Acta Math. Hungar. 146 (2015), 86–97.CrossRefGoogle Scholar
Tsang, K. M., The Distribution of the Values of the Riemann Zeta-function, PhD Thesis (Princeton University, 1984).Google Scholar
Xiao, X. and Zhai, S., ‘Discrepancy bounds for distribution of automorphic
$L$
-functions’, Lith. Math. J. 61 (2021), 550–563.CrossRefGoogle Scholar
$L$
-functions’, Lith. Math. J. 61 (2021), 550–563.CrossRefGoogle ScholarYe, Y. and Zhang, D., ‘Zero density for automorphic
$L$
-functions’, J. Number Theory 133 (2013), 3877–3901.CrossRefGoogle Scholar
$L$
-functions’, J. Number Theory 133 (2013), 3877–3901.CrossRefGoogle Scholar