Hostname: page-component-f554764f5-nwwvg Total loading time: 0 Render date: 2025-04-21T02:21:16.359Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIFFERENCE ANALOGUE OF THE TUMURA–HAYMAN–CLUNIE THEOREM

Part of: Difference and functional equations Difference equations Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  06 November 2023

MINGLIANG FANG Open the ORCID record for MINGLIANG FANG [Opens in a new window] ,
HUI LI Open the ORCID record for HUI LI [Opens in a new window]  and
XIAO YAO Open the ORCID record for XIAO YAO [Opens in a new window]
MINGLIANG FANG
Affiliation:
School of Sciences, Hangzhou Dianzi University, Hangzhou 310012, PR China e-mail: [email protected]
HUI LI*
Affiliation:
School of Science, China University of Mining and Technology-Beijing, Beijing 100083, PR China
XIAO YAO
Affiliation:
School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a difference analogue of the celebrated Tumura–Hayman–Clunie theorem. Let f be a transcendental entire function, let c be a nonzero constant and let n be a positive integer. If f and 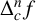$\Delta _c^n f$ omit zero in the whole complex plane, then either 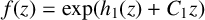$f(z)=\exp (h_1(z)+C_1 z)$, where 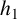$h_1$ is an entire function of period c and 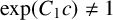$\exp (C_1 c)\neq 1$, or 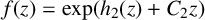$f(z)=\exp (h_2(z)+C_2 z)$, where 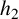$h_2$ is an entire function of period 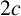$2c$ and 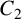$C_2$ satisfies

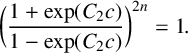$$ \begin{align*} \bigg(\frac{1+\exp(C_2c)}{1-\exp(C_2 c)}\bigg)^{2n}=1. \end{align*} $$

Keywords

entire functionsforward differencesvalue distribution

MSC classification

Primary: 30D35: Distribution of values, Nevanlinna theory
Secondary: 39A10: Difference equations, additive
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 1 , August 2024 , pp. 145 - 154
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was partially supported by the National Natural Science Foundation of China (Grant Nos. 12171127, 12071047, 12301096, 11901311, 12371074) and National Key Technologies R&D Program of China (2020YFA0713300).

References

Chen, Z. X., ‘Relationships between entire functions and their forward differences’, Complex Var. Elliptic Equ. 58(3) (2013), 299–307.Google Scholar
Chen, Z. X. and Shon, K. H., ‘Estimates for the zeros of differences of meromorphic functions’, Sci. China Ser. A 52(11) (2009), 2447–2458.Google Scholar
Chiang, Y. M. and Feng, S. J., ‘On the Nevanlinna characteristic of $f(z+\eta)$ and difference equations in the complex plane’, Ramanujan J. 16(1) (2008), 105–129.Google Scholar
Chiang, Y. M. and Feng, S. J., ‘On the growth of logarithmic differences, difference quotients and logarithmic derivatives of meromorphic functions’, Trans. Amer. Math. Soc. 361 (2009), 3767–3791.CrossRefGoogle Scholar
Clunie, J., ‘On integral and meromorphic functions’, J. Lond. Math. Soc. 37 (1962), 17–27.Google Scholar
Csillag, P., ‘Über ganze Funktionen, welehe drei nicht verschwindende Ableitungen besitzen’, Math. Ann. 110 (1935), 745–752.CrossRefGoogle Scholar
Frank, G., ‘Eine Vermutung von Hayman über Nullstellen meromorpher Funktionen’, Math. Z. 149 (1976), 29–36.CrossRefGoogle Scholar
Halburd, R. G. and Korhonen, R. J., ‘Difference analogue of the lemma on the logarithmic derivative with applications to difference equations’, J. Math. Anal. Appl. 314(2) (2006), 477–487.Google Scholar
Halburd, R. G. and Korhonen, R. J., ‘Nevanlinna theory for the difference operator’, Ann. Acad. Sci. Fenn. Math. 31(2) (2006), 463–478.Google Scholar
Halburd, R. G., Korhonen, R. J. and Tohge, K., ‘Holomorphic curves with shift-invariant hyperplane preimages’, Trans. Amer. Math. Soc. 366(8) (2014), 4267–4298.CrossRefGoogle Scholar
Hayman, W. K., ‘Picard values of meromorphic functions and their derivatives’, Ann. of Math. 70(2) (1959), 9–42.Google Scholar
Hayman, W. K., Meromorphic Functions, Oxford Mathematical Monographs, 3 (Clarendon Press, Oxford, 1964).Google Scholar
Langley, J. K., ‘Proof of a conjecture of Hayman concerning $f$ and ${f}^{{\prime\prime} }$ ’, J. Lond. Math. Soc. 48(2) (1993), 500–514.CrossRefGoogle Scholar
Pólya, G., ‘On an integral function of an integral function’, J. Lond. Math. Soc. 1(1) (1926), 12–15.Google Scholar
Tumura, Y., ‘On the extensions of Borel’s theorem and Saxer–Csillag’s theorem’, Proc. Phys. Math. Soc. Japan 19(3) (1937), 29–35.Google Scholar
Yang, C. C. and Yi, H. X., Uniqueness Theory of Meromorphic Functions (Kluwer Academic Publishers and Science Press, Dordrecht–Beijing–New York, 2003).Google Scholar
Yang, L., Value Distribution Theory (Springer, New York, 1993).Google Scholar