Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-26T06:57:30.988Z Has data issue: false hasContentIssue false
  • English
  • Français

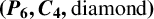THE CHROMATIC NUMBER OF $\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  03 October 2022

KAIYANG LAN Open the ORCID record for KAIYANG LAN [Opens in a new window] ,
YIDONG ZHOU Open the ORCID record for YIDONG ZHOU [Opens in a new window]  and
FENG LIU Open the ORCID record for FENG LIU [Opens in a new window]
KAIYANG LAN
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian 350003, PR China e-mail: [email protected]
YIDONG ZHOU
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian 350003, PR China e-mail: [email protected]
FENG LIU*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200241, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The diamond is the complete graph on four vertices minus one edge; 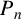$P_n$ and 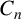$C_n$ denote the path and cycle on n vertices, respectively. We prove that the chromatic number of a $(P_6,C_4,\mbox {diamond})$-free graph G is no larger than the maximum of 3 and the clique number of G.

Keywords

chromatic numberinduced subgraphℱ-free graph

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C17: Perfect graphs 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was partially supported by a grant from the National Natural Sciences Foundation of China (No. 11971111).

References

Bondy, J. and Murty, U. S. R., Graph Theory, Graduate Texts in Mathematics, 244 (Springer, Berlin, 2008).CrossRefGoogle Scholar
Cameron, K., Huang, S. and Merkel, O., ‘An optimal $\chi$ -bound for ( ${P}_6$ , diamond)-free graphs’, J. Graph Theory 97 (2021), 451–465.CrossRefGoogle Scholar
Char, A. and Karthick, T., ‘Coloring of (P5, 4-wheel)-free graphs’, Discrete Math. 345 (2022), Article no 112795, 22 pages.CrossRefGoogle Scholar
Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R., ‘The strong perfect graph theorem’, Ann. of Math. (2) 164 (2006), 51–229.CrossRefGoogle Scholar
Chudnovsky, M. and Sivaraman, V., ‘Perfect divisibility and 2-divisibility’, J. Graph Theory 90 (2019), 54–60.CrossRefGoogle Scholar
Erdős, P., ‘Graph theory and probability’, Canad. J. Math. 11 (1959), 34–38.CrossRefGoogle Scholar
Gaspers, S. and Huang, S., ‘Linearly $\chi$ -bounding $\mathbf{\mathcal{H}}$ -free graphs’, J. Graph Theory 92 (2019), 322–342.CrossRefGoogle Scholar
Goedgebeur, J., Huang, S., Ju, Y. and Merkel, O., ‘Colouring graphs with no induced six-vertex path or diamond’, Preprint, 2021, arXiv:2106.08602v1.CrossRefGoogle Scholar
Gravier, S., Hoàng, C. and Maffray, F., ‘Coloring the hypergraph of maximal cliques of a graph with no long path’, Discrete Math. 272 (2003), 285–290.CrossRefGoogle Scholar
Gyárfás, A., ‘Problems from the world surrounding perfect graphs’, Zastos. Mat. XIX (1987), 413–441.Google Scholar
Karthick, T. and Maffray, F., ‘Vizing bound for the chromatic number on some graph classes’, Graphs Combin. 32 (2016), 1447–1460.CrossRefGoogle Scholar
Karthick, T. and Maffray, F., ‘Square-free graphs with no six-vertex induced path’, SIAM J. Discrete Math. 33 (2019), 874–909.CrossRefGoogle Scholar
Karthick, T. and Mishra, S., ‘On the chromatic number of ( ${P}_5$ , diamond)-free graphs’, Graphs Combin. 34 (2018), 677–692.CrossRefGoogle Scholar
Kierstead, H., Penrice, S. and Trotter, W., ‘On-line and first-fit coloring of graphs that do not induce ${P}_5$ ’, SIAM J. Discrete Math. 8 (1995), 485–498.CrossRefGoogle Scholar
Mycielski, J., ‘Sur le coloriage des graphes’, Colloq. Math. 3 (1955), 161–162.CrossRefGoogle Scholar
Schiermeyer, I., ‘Chromatic number of ${P}_5$ -free graphs: Reed’s conjecture’, Discrete Math. 343 (2016), 1940–1943.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘Induced subgraphs of graphs with large chromatic number. I. Odd holes’, J. Combin. Theory Ser. B 121 (2016), 68–84.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘A survey of $\chi$ -boundedness’, J. Graph Theory 95 (2020), 473–504.CrossRefGoogle Scholar
West, D., Introduction to Graph Theory, 2nd edn (Prentice-Hall, Englewood Cliffs, NJ, 2000).Google Scholar