Article contents
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS
Published online by Cambridge University Press: 07 June 2021
Abstract
Gireesh and Mahadeva Naika [‘On 3-regular partitions in 3-colors’, Indian J. Pure Appl. Math.50 (2019), 137–148] proved an infinite family of congruences modulo powers of 3 for the function
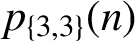 $p_{\{3,3\}}(n)$
, the number of 3-regular partitions in three colours. In this paper, using elementary generating function manipulations and classical techniques, we significantly extend the list of proven arithmetic properties satisfied by
$p_{\{3,3\}}(n)$
, the number of 3-regular partitions in three colours. In this paper, using elementary generating function manipulations and classical techniques, we significantly extend the list of proven arithmetic properties satisfied by
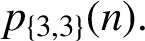 $p_{\{3,3\}}(n).$
$p_{\{3,3\}}(n).$
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 415 - 423
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the São Paulo Research Foundation (FAPESP) (grant no. 2019/14796-8).
References
- 3
- Cited by



