Hostname: page-component-6587cd75c8-2cm9h Total loading time: 0 Render date: 2025-04-24T08:59:37.227Z Has data issue: false hasContentIssue false
  • English
  • Français

AN IMPROVEMENT TO A THEOREM OF LEONETTI AND LUCA

Part of: Sequences and sets

Published online by Cambridge University Press:  01 September 2023

TRAN NGUYEN THANH DANH ,
HOANG TUAN DUNG ,
PHAM VIET HUNG ,
NGUYEN DINH KIEN ,
NGUYEN AN THINH ,
KHUC DINH TOAN  and
NGUYEN XUAN THO Open the ORCID record for NGUYEN XUAN THO [Opens in a new window]
TRAN NGUYEN THANH DANH
Affiliation:
VNU-HCM High School for the Gifted Students, Ho Chi Minh City, Vietnam e-mail: [email protected]
HOANG TUAN DUNG
Affiliation:
Hanoi National University of Education High School for the Gifted Students, Hanoi, Vietnam e-mail: [email protected]
PHAM VIET HUNG
Affiliation:
HUS High School for Gifted Students, Hanoi, Vietnam e-mail: [email protected]
NGUYEN DINH KIEN
Affiliation:
Tran Phu High School for the Gifted Students, Haiphong, Vietnam e-mail: [email protected]
NGUYEN AN THINH
Affiliation:
Tran Phu High School for the Gifted Students, Haiphong, Vietnam e-mail: [email protected]
KHUC DINH TOAN
Affiliation:
Bac Ninh High School for the Gifted Students, Báˇc Ninh, Vietnam e-mail: [email protected]
NGUYEN XUAN THO*
Affiliation:
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Vietnam
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Leonetti and Luca [‘On the iterates of the shifted Euler’s function’, Bull. Aust. Math. Soc., to appear] have shown that the integer sequence 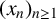$(x_n)_{n\geq 1}$ defined by 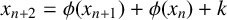$x_{n+2}=\phi (x_{n+1})+\phi (x_{n})+k$, where 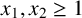$x_1,x_2\geq 1$, 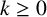$k\geq 0$ and 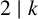$2 \mid k$, is bounded by 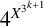$4^{X^{3^{k+1}}}$, where 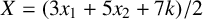$X=(3x_1+5x_2+7k)/2$. We improve this result by showing that the sequence 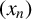$(x_n)$ is bounded by 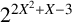$2^{2X^2+X-3}$, where 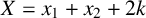$X=x_1+x_2+2k$.

Keywords

Euler’s totient functioninteger sequencerecursive sequence

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11B37: Recurrences
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 437 - 442
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Nguyen Xuan Tho is funded by the Vietnam Ministry of Education and Training under the project number B2022-CTT-03.

References

Aigner, M. and Ziegler, G. M., Proofs from The Book, 6th edn (Springer, Berlin, 2018).CrossRefGoogle Scholar
Erdős, P., ‘Beweis eines Satzes von Tschebyschef’, Acta Sci. Math. (Szeged) 5 (1930–1932), 194–198.Google Scholar
Leonetti, P. and Luca, F., ‘On the iterates of the shifted Euler’s function’, Bull. Aust. Math. Soc., to appear. Published online (12 May 2023).CrossRefGoogle Scholar
Rosser, J. B., ‘The $n$ -th prime is greater than $n \log n$ ’, Proc. Lond. Math. Soc. (3) 45 (1939), 21–44.CrossRefGoogle Scholar