Article contents
ADDITIVE BASES AND NIVEN NUMBERS
Published online by Cambridge University Press: 25 March 2021
Abstract
Let
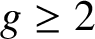 $g \geq 2$
be an integer. A natural number is said to be a base-g Niven number if it is divisible by the sum of its base-g digits. Assuming Hooley’s Riemann hypothesis, we prove that the set of base-g Niven numbers is an additive basis, that is, there exists a positive integer
$g \geq 2$
be an integer. A natural number is said to be a base-g Niven number if it is divisible by the sum of its base-g digits. Assuming Hooley’s Riemann hypothesis, we prove that the set of base-g Niven numbers is an additive basis, that is, there exists a positive integer
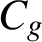 $C_g$
such that every natural number is the sum of at most
$C_g$
such that every natural number is the sum of at most
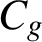 $C_g$
base-g Niven numbers.
$C_g$
base-g Niven numbers.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 373 - 380
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
C. Sanna is a member of GNSAGA of INdAM and of CrypTO, the group of Cryptography and Number Theory of Politecnico di Torino.
References
- 1
- Cited by



