Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-21T04:42:01.190Z Has data issue: false hasContentIssue false
  • English
  • Français

ADDITIVE AND SUBTRACTIVE BASES OF $\mathbb {Z}_m$ IN AVERAGE

Part of: Sequences and sets

Published online by Cambridge University Press:  25 November 2024

GUANGPING LIANG ,
YU ZHANG  and
HAODE ZUO Open the ORCID record for HAODE ZUO [Opens in a new window]
GUANGPING LIANG
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou 225002, PR China e-mail: [email protected]
YU ZHANG
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, PR China e-mail: [email protected]
HAODE ZUO*
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou 225002, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a positive integer m, let $\mathbb {Z}_m$ be the set of residue classes mod m. For 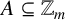$A\subseteq \mathbb {Z}_m$ and 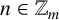$n\in \mathbb {Z}_m$, let 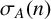$\sigma _A(n)$ be the number of solutions to the equation 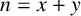$n=x+y$ with 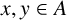$x,y\in A$. Let 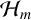$\mathcal {H}_m$ be the set of subsets 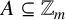$A\subseteq \mathbb {Z}_m$ such that 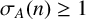$\sigma _A(n)\geq 1$ for all 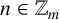$n\in \mathbb {Z}_m$. Let

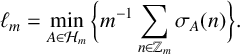$$ \begin{align*} \ell_m=\min\limits_{A\in \mathcal{H}_m}\bigg\lbrace m^{-1}\sum_{n\in \mathbb{Z}_m}\sigma_A(n)\bigg\rbrace. \end{align*} $$

Ding and Zhao [‘A new upper bound on Ruzsa’s numbers on the Erdős–Turán conjecture’, Int. J. Number Theory 20 (2024), 1515–1523] showed that 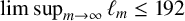$\limsup _{m\rightarrow \infty }\ell _m\le 192$. We prove

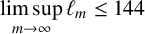$$ \begin{align*} \limsup\limits_{m\rightarrow\infty}\ell_m\leq 144 \end{align*} $$

and investigate parallel results on subtractive bases of $ \mathbb {Z}_m$.

Keywords

representation functionsRuzsa’s numbersprime number theoremadditive bases

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Borwein, P., Choi, S. and Chu, F., ‘An old conjecture of Erdős–Turán on additive bases’, Math. Comp. 75 (2006), 475–484.CrossRefGoogle Scholar
Chen, Y.-G., ‘The analogue of Erdős–Turán conjecture in ${\mathbb{Z}}_m$ ’, J. Number Theory 128 (2008), 2573–2581.CrossRefGoogle Scholar
Chen, Y.-G. and Sun, T., ‘The difference basis and bi-basis of ${\mathbb{Z}}_m$ ’, J. Number Theory 130 (2010), 716–726.CrossRefGoogle Scholar
Davenport, H., Multiplicative Number Theory, 2nd edn, Graduate Texts in Mathematics, 74 (Springer-Verlag, New York, 1980).CrossRefGoogle Scholar
Ding, Y. and Zhao, L., ‘A new upper bound on Ruzsa’s numbers on the Erdős–Turán conjecture’, Int. J. Number Theory 20 (2024), 1515–1523.CrossRefGoogle Scholar
Erdős, P. and Turán, P., ‘On a problem of Sidon in additive number theory, and on some related problems’, J. Lond. Math. Soc. (2) 16 (1941), 212–215.CrossRefGoogle Scholar
Evans, T. A. and Mann, H. B., ‘On simple difference sets’, Sankhyā 11 (1951), 357–364.Google Scholar
Grekos, G., Haddad, L., Helou, C. and Pihko, J., ‘On the Erdős–Turán conjecture’, J. Number Theory 102 (2003), 339–352.CrossRefGoogle Scholar
Guy, R. K., Unsolved Problems in Number Theory, 3rd edn, Problem Books in Mathematics, 1 (Springer-Verlag, New York, 2004).CrossRefGoogle Scholar
Halberstam, H. and Roth, K. F., Sequences (Clarendon Press, Oxford, 1966).Google Scholar
Hall, M. Jr, ‘Cyclic projective planes’, Duke Math. J. 14 (1947), 1079–1090.Google Scholar
Ruzsa, I. Z., ‘A just basis’, Monatsh. Math. 109 (1990), 145–151.CrossRefGoogle Scholar
Sándor, C. and Yang, Q.-H., ‘A lower bound of Ruzsa’s number related to the Erdős–Turán conjecture’, Acta Arith. 180 (2017), 161–169.CrossRefGoogle Scholar
Singer, J., ‘A theorem in finite projective geometry and some applications to number theory’, Trans. Amer. Math. Soc. 43 (1938), 377–385.CrossRefGoogle Scholar
Tang, M. and Chen, Y.-G., ‘A basis of ${\mathbb{Z}}_m$ ’, Colloq. Math. 104 (2006), 99–103.CrossRefGoogle Scholar
Tang, M. and Chen, Y.-G., ‘A basis of ${\mathbb{Z}}_m$ , II’, Colloq. Math. 108 (2007), 141–145.CrossRefGoogle Scholar
Tao, T. and Van Vu, H., Additive Combinatorics, Cambridge Studies in Advanced Mathematics, 105 (Cambridge University Press, Cambridge, 2010).Google Scholar
Zhang, Y., ‘On the difference bases of ${\mathbb{Z}}_m$ ’, Period. Math. Hungar., to appear. Published online (10 July 2024).CrossRefGoogle Scholar