Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T14:47:08.622Z Has data issue: false hasContentIssue false
  • English
  • Français

Two Applications of Inner Model Theory to the Study of 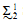Sets

Published online by Cambridge University Press:  15 January 2014

Greg Hjorth
Greg Hjorth*
Affiliation:
Department of mathematics, University of California, Los Angeles, Los Angeles, CA 90095-1555, USAE-mail: , [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

§0. Preface. There has been an expectation that the endgame of the more tenacious problems raised by the Los Angeles ‘cabal’ school of descriptive set theory in the 1970's should ultimately be played out with the use of inner model theory. Questions phrased in the language of descriptive set theory, where both the conclusions and the assumptions are couched in terms that only mention simply definable sets of reals, and which have proved resistant to purely descriptive set theoretic arguments, may at last find their solution through the connection between determinacy and large cardinals.

Perhaps the most striking example was given by [24], where the core model theory was used to analyze the structure of HOD and then show that all regular cardinals below ΘL(ℝ) are measurable. John Steel's analysis also settled a number of structural questions regarding HODL(ℝ), such as GCH.

Another illustration is provided by [21]. There an application of large cardinals and inner model theory is used to generalize the Harrington-Martin theorem that 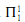determinacy implies 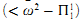)determinacy.

However, it is harder to find examples of theorems regarding the structure of the projective sets whose only known proof from determinacy assumptions uses the link between determinacy and large cardinals. We may equivalently ask whether there are second order statements of number theory that cannot be proved under PD–the axiom of projective determinacy–without appealing to the large cardinal consequences of the PD, such as the existence of certain kinds of inner models that contain given types of large cardinals.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 2 , Issue 1 , March 1996 , pp. 94 - 107
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions, to appear in the London Mathematical Society Lecture Note Series.Google Scholar
[2] Dodd, A., The core model, London Mathematical Society Lecture Note Series, vol. 61, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[3] Harrington, L. A., Analytic determinacy and 0# , Journal of Symbolic Logic, vol. 43 (1978), pp. 685–693.Google Scholar
[4] Hjorth, G., Some applications of coarse inner model theory, preprint, Caltech, 1994.Google Scholar
[5] Hjorth, G., Uncountable sets of reals, handwritten note, 1994.Google Scholar
[6] Jackson, S., Partition properties and well-ordered unions, Annals of Pure and Applied Logic, vol. 48 (1990), pp. 81–101.CrossRefGoogle Scholar
[7] Jackson, S. and Martin, D. A., Pointclasses and well-ordered unions, Cabal seminar 79–81 (Kechris, A. S., Martin, D. A., and Moschovakis, Y. N., editors), Lecture Notes in Mathematics 1019, Springer-Verlag, Berlin and New York, 1983, pp. 56–66.Google Scholar
[8] Jech, T., Set theory, Academic Press, London, 1978.Google Scholar
[9] Kanamori, A., The higher infinite, Springer-Verlag, Berlin and New York, 1994.Google Scholar
[10] Kanovei, V., Undecidable and decidable propertiesof constituents, Mathematics of USSR Sbornik, vol. 124 (1984), pp. 491–519.Google Scholar
[11] Kechris, A. S., A basis theorem for Borel sets, handwritten note, 1978.Google Scholar
[12] Kechris, A. S., On transfinite sequences of projective sets with an application to sets, Logic Colloquium '77 (Macintyre, A., Pacholski, L., and Paris, J., editors), North-Holland, Amsterdam, 1978, pp. 155–160.Google Scholar
[13] Kechris, A. S. and Martin, D. A., On the theory of sets of real, Bulletin of the American Mathematical Society, vol. 260 (1980), pp. 363–378.Google Scholar
[14] Kechris, A. S., Martin, D. A., and Solovay, R.M., Q-theory, Cabal seminar 79–81 (Kechris, A. S., Martin, D. A., and Moschovakis, Y. N., editors), Lecture Notes in Mathematics 1019, Springer-Verlag, Berlin and New York, 1983, pp. 199–281.CrossRefGoogle Scholar
[15] Louveau, A., A basis theorem for , handwritten note, 1978.Google Scholar
[16] Louveau, A., A separation theorem for sets, Transactions of the American Mathematical Society, vol. 260 (1980), pp. 363–378.Google Scholar
[17] Martin, D. A. and Steel, J. R., Iteration trees, Journal of the American Mathematical Society, vol. 7 (1994), pp. 1–72.CrossRefGoogle Scholar
[18] Miller, A. W., Arnie Miller's problem list, Israel Mathematics Conference Proceedings, vol. 6 (1993), pp. 645–654.Google Scholar
[19] Mitchell, W. and Steel, J. R., The fine structure of iteration trees, Lecture notes in Logic, no. 3, Springer-Verlag, Berlin, 1994.Google Scholar
[20] Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[21] Neeman, I., Optimal proofs of determinacy, this Bulletin, vol. 1 (1995), pp. 327–339.Google Scholar
[22] Schimmerling, E., Notes on some lectures by Woodin, Berkeley, 1990.Google Scholar
[23] Steel, J. R., The core model iterability problem, to appear in the Lecture Notes in Logic Series.Google Scholar
[24] Steel, J. R., HOD L(ℝ) is a core model, this Bulletin, vol. 1 (1995), pp. 75–84.Google Scholar
[25] Stern, J., On Lusin's restricted continuum problem, Annals of Mathematics, vol. 120 (1984), pp. 7–37.Google Scholar