No CrossRef data available.
Some Progress on the Unique Ergodicity Problem
Published online by Cambridge University Press: 28 February 2022
Abstract
This thesis is at the intersection of dynamics, probability and model theory. It focuses on a specialization of the notion of amenability: unique ergodicity.
Let G be a Polish group, i.e., a topological group whose topology is separable and completely metrizable. We call a G-flow the action of G on a compact space. A G-flow is said to be minimal if every orbit is dense.
A famous theorem of Ellis states that any Polish group G admits a unique universal minimal flow that we denote 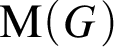 ${\mathrm {M}}(G)$
. This means that for any minimal G-flow X there is a surjective G-map from
${\mathrm {M}}(G)$
. This means that for any minimal G-flow X there is a surjective G-map from 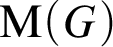 ${\mathrm {M}}(G)$
to X. G is said to be amenable if every G-flow admits an invariant probability measure, and uniquely ergodic if every minimal flow admits a unique invariant probability measure.
${\mathrm {M}}(G)$
to X. G is said to be amenable if every G-flow admits an invariant probability measure, and uniquely ergodic if every minimal flow admits a unique invariant probability measure.
The notion of unique ergodicity relating to a group was introduced by Angel, Kechris and Lyons. They also ask the following question which is the main focus of the thesis: Let G be an amenable Polish group with metrizable universal minimal flow, is G uniquely ergodic?
Note that unique ergodicity is an interesting notion only for relatively large groups, as it is proved in the last chapter of this thesis that locally compact non compact Polish groups are never uniquely ergodic. This result is joint work with Andy Zucker.
The thesis includes proofs of unique ergodicity of groups with interesting universal minimal flows, namely the automorphism group of the semigeneric directed graph and the automorphism group of the 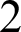 $2$
-graph.
$2$
-graph.
It also includes a theorem stating that under some hypothesis on a  $\omega $
-categorical structure M, the logic action of
$\omega $
-categorical structure M, the logic action of 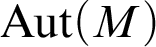 ${\mathrm {Aut}}(M)$
on
${\mathrm {Aut}}(M)$
on 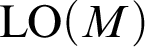 ${\mathrm {LO}}(M)$
, the compact space of linear orders on M, is uniquely ergodic. This implies unique ergodicity for the group if its universal minimal flow happens to be the space of linear orderings. It can also be used to prove non-amenability of some groups for which the action of
${\mathrm {LO}}(M)$
, the compact space of linear orders on M, is uniquely ergodic. This implies unique ergodicity for the group if its universal minimal flow happens to be the space of linear orderings. It can also be used to prove non-amenability of some groups for which the action of 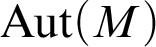 ${\mathrm {Aut}}(M)$
on
${\mathrm {Aut}}(M)$
on 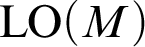 ${\mathrm {LO}}(M)$
is not minimal. This result is joint work with Todor Tsankov.
${\mathrm {LO}}(M)$
is not minimal. This result is joint work with Todor Tsankov.
Finally, the thesis also presents a proof that under the assumption that the universal minimal flows involved are metrizable, unique ergodicity is stable under group extensions. This result is joint work with Andy Zucker.
Abstract prepared by Colin Jahel.
E-mail: [email protected]
- Type
- Thesis Abstracts
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Association for Symbolic Logic
Footnotes
Supervised by Lionel Nguyen Van Thé and Todor Tsankov.



