Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T01:10:13.807Z Has data issue: false hasContentIssue false
  • English
  • Français

REDUCTION TECHNIQUES FOR PROVING DECIDABILITY IN LOGICS AND THEIR MEET–COMBINATION

Part of: General logic

Published online by Cambridge University Press:  06 May 2021

JOÃO RASGA ,
CRISTINA SERNADAS  and
WALTER CARNIELLI
JOÃO RASGA
Affiliation:
DEPARTAMENTO DE MATEMÁTICA INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE DE LISBOA, LISBOA, PORTUGALE-mail: [email protected]: https://fenix.tecnico.ulisboa.pt/homepage/ist14184
CRISTINA SERNADAS
Affiliation:
INSTITUTO DE TELECOMUNICAÇÕESLISBOA, PORTUGALE-mail: [email protected]: https://fenix.tecnico.ulisboa.pt/homepage/ist12466
WALTER CARNIELLI
Affiliation:
CENTRE FOR LOGIC EPISTEMOLOGY AND THE HISTORY OF SCIENCE UNIVERSITY OF CAMPINAS—UNICAMP, CAMPINAS, BRAZILE-mail: [email protected]: https://www.cle.unicamp.br/prof/carnielli/
Get access Rights & Permissions [Opens in a new window]

Abstract

Satisfaction systems and reductions between them are presented as an appropriate context for analyzing the satisfiability and the validity problems. The notion of reduction is generalized in order to cope with the meet-combination of logics. Reductions between satisfaction systems induce reductions between the respective satisfiability problems and (under mild conditions) also between their validity problems. Sufficient conditions are provided for relating satisfiability problems to validity problems. Reflection results for decidability in the presence of reductions are established. The validity problem in the meet-combination is proved to be decidable whenever the validity problem for the components are decidable. Several examples are discussed, namely, involving modal and intuitionistic logics, as well as the meet-combination of 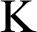$\textrm {K}$ modal logic and intuitionistic logic.

Keywords

meet-combination of logicsreductiondecidability

MSC classification

Primary: 03B25: Decidability of theories and sets of sentences
Secondary: 03B45: Modal logic (including the logic of norms) 03B62: Combined logics
Type
Articles
Information
Bulletin of Symbolic Logic , Volume 27 , Issue 1 , March 2021 , pp. 39 - 66
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agudelo-Agudelo, J. C. and Carnielli, W., Polynomial ring calculus for modalities . Journal of Logic and Computation, vol. 27 (2017), no. 6, pp. 1853–1870.Google Scholar
Barwise, J., Axioms for abstract model theory. Annals for Mathematical Logic, vol. 7 (1974), pp. 221–265.10.1016/0003-4843(74)90016-3CrossRefGoogle Scholar
Bezhanishvili, N. and de Jongh, D., Lecture Notes in Intuitionistic Logic. Presented at the ESSLLI 2005, Edinburgh, 2005.Google Scholar
Blackburn, P. and van Benthem, J., Modal logic: A semantic perspective, Handbook of Modal Logic (Blackburn, P., van Benthem, J., and Wolter, F., editors), Elsevier, Amsterdam, 2006, pp. 173–204.Google Scholar
Blackburn, P., de Rijke, M., and Venema, Y., Modal Logic, Cambridge University Press, Cambridge, 2001.10.1017/CBO9781107050884CrossRefGoogle Scholar
Börger, E., Grädel, E., and Gurevich, Y., The Classical Decision Problem , Springer, New York, 2001.Google Scholar
Carnielli, W. and Coniglio, M., Paraconsistent Logic: Consistency, Contradiction and Negation, Logic, Epistemology, and the Unity of Science, vol. 40, Springer, New York, 2016.Google Scholar
Carnielli, W., Coniglio, M., Gabbay, D., Gouveia, P., and Sernadas, C., Analysis and Synthesis of Logics—How to Cut and Paste Reasoning Systems, Springer, New York, 2008.Google Scholar
Chagrov, A. and Zakharyaschev, M., Modal Logic, Oxford University Press, Oxford, UK, 1997.Google Scholar
Ebbinghaus, H. D. and Flum, J., Finite Model Theory , Springer, Oxford, 1999.Google Scholar
Epstein, R. L. and Carnielli, W. A.. Computability: Computable Functions, Logic and the Foundations of Mathematics, Advanced Reasoning Forum, 2008.Google Scholar
Gabbay, D. M., Fibring Logics, Oxford University Press, Oxford, 1999.Google Scholar
Gödel, K., Collected Works, vol. I, Oxford University Press, Oxford, 1986.Google Scholar
Goldblatt, R., Mathematics of Modality , Stanford University Press, Redwood City, CA, 1993.Google Scholar
Gottwald, S., A Treatise on Many-Valued Logics , Research Studies Press, Baldock, 2001.Google Scholar
Grädel, E., Kolaitis, P. G., and Vardi, M.Y., On the decision problem for two-variable first-order logic, this Journal, vol. 3 (1997), no. 1, pp. 53–69.Google Scholar
Griffor, E. (ed.), Handbook of Computability Theory, North-Holland, Amsterdam, 1999.Google Scholar
Hilbert, D. and Ackermann, W.. Grundzüge der theoretischen Logik, fifth ed. Springer, New York, 1972.Google Scholar
Hilbert, D. and Ackermann, W.. Principles of Mathematical Logic, American Mathematical Society, Providence, RI, 2003.Google Scholar
Kleene, S. C., General recursive functions of natural numbers . Mathematische Annalen, vol. 112 (1936), no. 1, pp. 727–742.10.1007/BF01565439CrossRefGoogle Scholar
Kleene, S. C.,, Introduction to Metamathematics, Wolters-Noordhoff, Groningen, 1952.Google Scholar
Kracht, M. and Wolter, F., Properties of independently axiomatizable bimodal logics. The Journal of Symbolic Logic, vol. 56 (1991), no. 4, pp. 1469–1485.10.2307/2275487CrossRefGoogle Scholar
Libkin, L., Elements of Finite Model Theory, Springer, New York, 2004.10.1007/978-3-662-07003-1CrossRefGoogle Scholar
Mortimer, M., On languages with two variables . Mathematical Logic Quarterly, vol. 21 (1975), no. 1, pp. 135–140.10.1002/malq.19750210118CrossRefGoogle Scholar
Rasga, J., Sernadas, C., and Sernadas, A., Preservation of admissible rules when combining logics . The Review of Symbolic Logic, vol. 9 (2016), no. 4, pp. 641–663.10.1017/S1755020316000241CrossRefGoogle Scholar
Rogers, H. Jr. Theory of Recursive Functions and Effective Computability, second ed., MIT Press, Cambridge, MA, 1987.Google Scholar
Rybakov, V. V., Admissibility of Logical Inference Rules , North-Holland, Amsterdam, 1997.Google Scholar
Sernadas, A. and Sernadas, C., Foundations of Logic and Theory of Computation, second ed., College Publications, London, 2012.Google Scholar
Sernadas, A., Sernadas, C., and Caleiro, C., Synchronization of logics. Studia Logica, vol. 59 (1997), no. 2, pp. 217–247.10.1023/A:1004904401346CrossRefGoogle Scholar
Sernadas, A., Sernadas, C., and Rasga, J., On meet-combination of logics. Journal of Logic and Computation, vol. 22 (2012), no. 6, pp. 1453–1470.10.1093/logcom/exr035CrossRefGoogle Scholar
Sernadas, A., Sernadas, C., Rasga, J., and Ramos, J., A Mathematical Primer on Computability, College Publications, London, 2018.Google Scholar
Sernadas, C., Rasga, J., and Carnielli, W. A., Modulated fibring and the collapsing problem . The Journal of Symbolic Logic , vol. 67 (2002), no. 4, pp. 1541–1569.10.2178/jsl/1190150298CrossRefGoogle Scholar
Shoenfield, J. R., Recursion Theory , Springer, New York, 1993.10.1007/978-3-662-22378-9CrossRefGoogle Scholar
Soare, R. I., Turing Computability, Theory and Applications of Computability, Springer, New York, 2016.10.1007/978-3-642-31933-4CrossRefGoogle Scholar
Turing, A. M., Systems of logic based on ordinals . Proceedings of the London Mathematical Society, vol. 45 (1939), no. 3, pp. 161–228.10.1112/plms/s2-45.1.161CrossRefGoogle Scholar
Zanardo, A., Sernadas, A., and Sernadas, C., Fibring: Completeness preservation . The Journal of Symbolic Logic , vol. 66 (2001), no. 1, pp. 414–439.10.2307/2694931CrossRefGoogle Scholar