Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T02:29:44.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Proper Forcing and Remarkable Cardinals

Published online by Cambridge University Press:  15 January 2014

Ralf-Dieter Schindler
Ralf-Dieter Schindler*
Affiliation:
Institut Für Formale Logik, Universitát Wien, 1090 Wien, Austria E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The present paper investigates the power of proper forcings to change the shape of the universe, in a certain well-defined respect. It turns out that the ranking among large cardinals can be used as a measure for that power. However, in order to establish the final result I had to isolate a new large cardinal concept, which I dubbed “remarkability.” Let us approach the exact formulation of the problem—and of its solution—at a slow pace.

Breathtaking developments in the mid 1980s found one of its culminations in the theorem, due to Martin, Steel, and Woodin, that the existence of infinitely many Woodin cardinals with a measurable cardinal above them all implies that AD, the axiom of determinacy, holds in the least inner model containing all the reals, L(ℝ) (cf. [6[, p. 91). One of the nice things about AD is that the theory ZF + AD + V = L(ℝ) appears as a choiceless “completion” of ZF in that any interesting question (in particular, about sets of reals) seems to find an at least attractive answer in that theory (cf., for example, [5] Chap. 6). (Compare with ZF + V = L!) Beyond that, AD is very canonical as may be illustrated as follows.

Let us say that L(ℝ) is absolute for set-sized forcings if for all posets P ∈ V, for all formulae ϕ, and for all 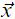∈ ℝ do we have that

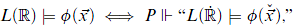
where is a name for the set of reals in the extension.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 6 , Issue 2 , June 2000 , pp. 176 - 184
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bagaria, J. and Woodin, H., sets of reals, The Journal of Symbolic Logic, vol. 62 (1997), pp. 1379–1428.Google Scholar
[2] Beller, A., Jensen, R., and Welch, Ph., Coding the universe, Cambridge, 1982.Google Scholar
[3] Foreman, M. and Magidor, M., Large cardinals and definable counterexamples to the continuum hypothesis, Annals of Pure and Applied Logic, vol. 76 (1995), pp. 47–97.Google Scholar
[4] Jensen, R. and Solovay, R., Some applications of almost disjoint sets, Mathematical logic and foundations of set theory (Bar-Hillel, , editor), North-Holland, 1970, pp. 84–104.Google Scholar
[5] Kanamori, A., The higher infinite, Springer-Verlag, 1994.Google Scholar
[6] Martin, D. and Steel, J., A proof of projective determinacy, Journal of the American Mathematical Society, vol. 2 (1989), pp. 71–125.Google Scholar
[7] Neeman, I. and Zapletal, J., Proper forcing and L(ℝ), preprint.Google Scholar
[8] Neeman, I. and Zapletal, J., Proper forcing and absoluteness in L(ℝ), Commentationes Mathematicae Universitatis Carolinae, vol. 39 (1998), pp. 281–301.Google Scholar
[9] Schindler, R.-D., Coding into K by reasonable forcing, to appear in Transactions of the American Mathematical Society.Google Scholar
[10] Neeman, I. and Zapletal, J., Proper forcing and remarkable cardinals II, to appear in Journal of Symbolic Logic.Google Scholar
[11] Shelah, S., Proper forcing, Springer-Verlag, 1982.Google Scholar
[12] Steel, J., Core models with more Woodin cardinals, preprint.Google Scholar
[13] Steel, J., Inner models with many Woodin cardinals, Annals of Pure and Applied Logic, vol. 65 (1993), pp. 185–209.Google Scholar
[14] Woodin, H., Lecture in the spring of 1990, notes taken by Burke, D. and Schimmerling, E..Google Scholar
[15] Woodin, H., The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter, 1999.Google Scholar