Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T12:42:28.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordered Groups: A Case Study in Reverse Mathematics

Published online by Cambridge University Press:  15 January 2014

Reed Solomon
Reed Solomon*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Madison, WI 57305, USA, E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The fundamental question in reverse mathematics is to determine which set existence axioms are required to prove particular theorems of mathematics. In addition to being interesting in their own right, answers to this question have consequences in both effective mathematics and the foundations of mathematics. Before discussing these consequences, we need to be more specific about the motivating question.

Reverse mathematics is useful for studying theorems of either countable or essentially countable mathematics. Essentially countable mathematics is a vague term that is best explained by an example. Complete separable metric spaces are essentially countable because, although the spaces may be uncountable, they can be understood in terms of a countable basis. Simpson (1985) gives the following list of areas which can be analyzed by reverse mathematics: number theory, geometry, calculus, differential equations, real and complex analysis, combinatorics, countable algebra, separable Banach spaces, computability theory, and the topology of complete separable metric spaces. Reverse mathematics is less suited to theorems of abstract functional analysis, abstract set theory, universal algebra, or general topology.

Section 2 introduces the major subsystems of second order arithmetic used in reverse mathematics: RCA0, WKL0, ACA0, ATR0 and 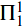– CA0. Sections 3 through 7 consider various theorems of ordered group theory from the perspective of reverse mathematics. Among the results considered are theorems on ordered quotient groups (including an equivalent of ACA0), groups and semigroup conditions which imply orderability (WKL0), the orderability of free groups (RCA0), Hölder's Theorem (RCA0), Mal'tsev's classification of the order types of countable ordered groups ( 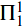– CA0)

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 5 , Issue 1 , March 1999 , pp. 45 - 58
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baumslag, G., Cannonito, F., Robinson, D. and Segal, D. (1991), The algorithmic theory of polycyclic-by-finite groups, Journal of Algebra, vol. 141, pp. 118–149.Google Scholar
Brown, D. K. and Simpson, S.G. (1986), Which set existence axioms are needed to prove the separable Hahn–Banach Theorem?, Annals of Pure and Applied Logic, vol. 31, pp. 123–144.Google Scholar
Downey, R. and Kurtz, S. A. (1986), Recursion theory and ordered groups, Annals of Pure and Applied Logic, vol. 32, pp. 137–151.Google Scholar
Drake, F. R. (1989), On the foundations of mathematics in 1987, Logic Colloquium 87, Studies in Logic, vol. 129, North–Holland, pp. 11–25.Google Scholar
Feferman, S. (1988), Hilbert's program relativized: proof theoretical and foundational reductions, Journal of Symbolic Logic, vol. 53, no. 2, pp. 364–384.Google Scholar
Friedman, H. (1976), Systems of second order arithmetic with restricted induction i, ii, Journal of Symbolic Logic, vol. 41, pp. 557–559, (abstracts).Google Scholar
Friedman, H. M. and Hirst, J. L. (1990), Weak comparability of well orderings and reverse mathematics, Annals of Pure and Applied Logic, vol. 47, pp. 11–29.Google Scholar
Friedman, H. M., Simpson, S. G. and Smith, R. L. (1983), Countable algebra and set existence axioms, Annals of Pure and Applied Logic, vol. 25, pp. 141–181.Google Scholar
Fuchs, L. (1958), Note on ordered groups and rings, Fundamenta Mathematicae, vol. 46, pp. 167–174.CrossRefGoogle Scholar
Fuchs, L. (1963), Partially ordered algebraic systems, Pergamon Press.Google Scholar
Hatzikiriakou, K. (1989), Algebraic disguises of induction, Archive for Mathematical Logic, vol. 29, no. 4, pp. 47–51.Google Scholar
Hatzikiriakou, K. and Simpson, S. G. (1990), WKL0 and orderings of countable abelian groups, Contemporary Mathematics, vol. 106, pp. 177–180.CrossRefGoogle Scholar
Hirst, J. L. (1994), Reverse mathematics and ordinal exponentiation, Annals of Pure and Applied Logic, vol. 66, pp. 1–18.Google Scholar
Jockusch, C.G. Jr. and Soare, R. I. (1972), classes and degrees of theories, Transactions of the American Mathematical Society, vol. 173, pp. 33–56.Google Scholar
Kokorin, A. and Kopytov, V. (1974), Fully ordered groups, Halsted Press.Google Scholar
Kreisel, G. (1959), Analysis of the Cantor–Bendixson theorem by means of the analytic hierarchy, Bull. Acad. Polon. Sci., vol. 7, pp. 621–626.Google Scholar
Lorenzen, P. (1949), Über halbgeordnete gruppen, Archiv der Mathematik, vol. 2, pp. 66–70, (German).Google Scholar
Łos, J. (1954), On the existence of linear order in a group, Bull. Acad. Polon. Sci. Cl. III, vol. 2, pp. 21–23.Google Scholar
Mal'tsev, A. (1949), On ordered groups, Izvestiya Akademii Nauk USSR Seriya Matematicheskaya, vol. 13, pp. 473–482, (Russian).Google Scholar
Metakides, G. and Nerode, A. (1979), Effective content of field theory, Annals of Mathematical Logic, vol. 17, pp. 289–320.CrossRefGoogle Scholar
Ohnishi, M. (1952), Linear order on a group, Osaka Mathematical Journal, vol. 4, pp. 17–18.Google Scholar
Parsons, C. (1970), On a number theoretic choice scheme and its relation to induction, Intuitionism and Proof Theory (Kino, A. et al., editors), North–Holland, pp. 459–474.Google Scholar
Rabin, M. (1960), Computable algebra, general theory and theory of computable fields, Transactions of the American Mathematical Society, vol. 95, pp. 341–360.Google Scholar
Revesz, G. (1986), Full orders on free groups, Algebra and Order: Proceedings of the First International Symposium for Ordered Algebraic Structures Luminy–Marseille 1984 (Wolfenstein, S., editor).Google Scholar
Simpson, S. G. (1984), Which set existence axioms are needed to prove the Cauchy/Peano Theorem for ordinary differential equations?, Journal of Symbolic Logic, vol. 49, pp. 783–802.CrossRefGoogle Scholar
Simpson, S. G. (1985), Reverse mathematics, Proceedings of Symposia in Pure Mathematics, vol. 42, pp. 461–471.Google Scholar
Simpson, S. G. (1988), Partial realizations of hilbert's program, Journal of Symbolic Logic, vol. 53, no. 2, pp. 349–363.Google Scholar
Simpson, S. G. (1998), Subsystems of second order arithmetic, Springer-Verlag.Google Scholar
Soare, R. I. (1987), Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer–Verlag.Google Scholar
Solomon, D. R. (1998), Reverse mathematics and ordered groups, Ph.D. thesis , Cornell University.Google Scholar
Teh, H. (1960), Construction of orders in abelian groups, Cambridge Philosophical Society Proceedings, vol. 57, pp. 476–482.Google Scholar