Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T00:53:41.815Z Has data issue: false hasContentIssue false
  • English
  • Français

The Mathematical Import of Zermelo's Well-Ordering Theorem

Published online by Cambridge University Press:  15 January 2014

Akihiro Kanamori
Akihiro Kanamori*
Affiliation:
Department of Mathematics, Boston University, Boston, MA 02215, USA.E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Set theory, it has been contended, developed from its beginnings through a progression of mathematical moves, despite being intertwined with pronounced metaphysical attitudes and exaggerated foundational claims that have been held on its behalf. In this paper, the seminal results of set theory are woven together in terms of a unifying mathematical motif, one whose transmutations serve to illuminate the historical development of the subject. The motif is foreshadowed in Cantor's diagonal proof, and emerges in the interstices of the inclusion vs. membership distinction, a distinction only clarified at the turn of this century, remarkable though this may seem. Russell runs with this distinction, but is quickly caught on the horns of his well-known paradox, an early expression of our motif. The motif becomes fully manifest through the study of functions 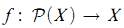of the power set of a set into the set in the fundamental work of Zermelo on set theory. His first proof in 1904 of his Well-Ordering Theoremis a central articulation containing much of what would become familiar in the subsequent development of set theory. Afterwards, the motif is cast by Kuratowski as a fixed point theorem, one subsequently abstracted to partial orders by Bourbaki in connection with Zorn's Lemma. Migrating beyond set theory, that generalization becomes cited as the strongest of fixed point theorems useful in computer science.

Section 1 describes the emergence of our guiding motif as a line of development from Cantor's diagonal proof to Russell's Paradox, fueled by the clarification of the inclusion vs. membership distinction. Section 2 engages the motif as fully participating in Zermelo's work on the Well-Ordering Theorem and as newly informing on Cantor's basic result that there is no bijection 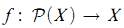. Then Section 3 describes in connection with Zorn's Lemma the transformation of the motif into an abstract fixed point theorem, one accorded significance in computer science.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 3 , Issue 3 , September 1997 , pp. 281 - 311
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1977] Aczel, Peter, An introduction to inductive definitions, Handbook of mathematical logic (Barwise, K. Jon, editor), North-Holland, Amsterdam, pp. 739–782.Google Scholar
[1922] Banach, Stefan, Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales, Fundamenta Mathematicae, vol. 3, pp. 133–181.Google Scholar
[1995] Bell, John L., Type reducing correspondences and well-orderings: Frege's and Zermelo's constructions re-examined, The Journal of Symbolic Logic, vol. 60, pp. 209–221.CrossRefGoogle Scholar
[1954] Bernays, Paul, A system of axiomatic set theory VII, The Journal of Symbolic Logic, vol. 19, pp. 81–96.CrossRefGoogle Scholar
[1997] Boolos, George, Constructing Cantorian counterexamples, Journal of Philosophical Logic, vol. 26, pp. 237–239.Google Scholar
[1898] Borel, Emile, Leçons sur la théorie des fonctions, Gauthier-Villars, Paris.Google Scholar
[1939] Bourbaki, Nicolas, Eléments de mathématique. I. Théorie des ensembles. Fascicule de résultats, Actualités Scientifiques et Industrielles, no. 846, Hermann, Paris.Google Scholar
[1949/1950] Bourbaki, Nicolas, Sur le théoreme de Zorn, Archiv der Mathematik, vol. 2, pp. 434–437.CrossRefGoogle Scholar
[1956] Bourbaki, Nicolas, Eléments de mathématique. I. Théorie des ensembles. Chapter III: Ensembles ordonnés, cardinaux, nombres entiers, Actualités Scientifiques et Industrielles, no. 1243, Hermann, Paris.Google Scholar
[1909] Brouwer, Luitzen E. J., On continuous one-one transformations of surfaces into themselves, Koninklijke Nederlandse Akademie van Wetenschappen te Amsterdam, Proceedings, vol. 11, reprinted in [1976] below, pp. 195–206.Google Scholar
[1976] Brouwer, Luitzen E. J., Collected works (Freudenthal, Hans, editor), vol. 2, North-Holland, Amsterdam.Google Scholar
[1897] Burali-Forti, Cesare, Una questione sui numeri transfini, Rendiconti del Circolo Matematico di Palermo, vol. 11, pp. 154–164, translated in van Heijenoort [1967], pp. 104–111.Google Scholar
[1978] Campbell, Paul J., The origin of “Zorn's lemma”, Historia Mathematica, vol. 5, pp. 77–89.Google Scholar
[1874] Cantor, Georg, Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, Journal für die reine und angewandte Mathematik (Crelle's Journal), vol. 77, pp. 258–262, reprinted in [1932] below, pp. 115–118.Google Scholar
[1883] Cantor, Georg, Über unendliche, lineare punktmannigfaltigkeiten. V, Mathematische Annalen, vol. 21, pp. 545–591, published separately as Grundlagen einer allgemeinen Mannigfaltigkeitslehre. Ein mathematisch-philosophischer Versuch in der Lehre des Unendlichen , B. G. Teubner, Leipzig, 1883; reprinted in [1932] below, pp. 165–209.Google Scholar
[1891] Cantor, Georg, Über eine elementare Frage der Mannigfaltigkeitslehre, Jahresbericht der Deutschen Mathematiker-Vereinigung, vol. 1, pp. 75–78, reprinted in [1932] below, pp. 278–280.Google Scholar
[1895] Cantor, Georg, Beiträge zur Begründung der transfiniten Mengenlehre. I, Mathematische Annalen, vol. 46, pp. 481–512, translated in [1915] below; reprinted in [1932] below, pp. 282–311.Google Scholar
[1897] Cantor, Georg, Beiträge zur Begründung der transfiniten Mengenlehre. II, Mathematische Annalen, vol. 49, pp. 207–246, translated in [1915] below; reprinted in [1932] below, pp. 312–351.Google Scholar
[1915] Cantor, Georg, Contributions to the founding of the theory of transfinite numbers, Open Court, Chicago, translation of [1895] and [1897] above with introduction and notes by Philip E. B. Jourdain; reprinted Dover, New York, 1965.Google Scholar
[1932] Cantor, Georg, Gesammelte Abhandlungen mathematicschen und philosophischen Inhalts (Zermelo, Ernst, editor), Julius Springer, Berlin, reprinted in Springer-Verlag, Berlin, 1980.CrossRefGoogle Scholar
[1962] Cavaillès, Jean, Philosophie mathématique, Hermann, Paris, includes French translation of Noether-Cavailles [1937].Google Scholar
[1899] Couturat, Louis, La logique mathématique de M. Peano, Revue de Métaphysique et de Morale, vol. 7, pp. 616–646.Google Scholar
[1973] Crossley, John N., A note on Cantor's theorem and Russell's paradox, Australasian Journal of Philosophy, vol. 51, pp. 70–71.Google Scholar
[1990] Davey, Brian A. and Priestley, Hilary A., Introduction to lattices and order, Cambridge University Press, Cambridge.Google Scholar
[1888] Dedekind, Richard, Was sind und was sollen die Zahlen?, F. Vieweg, Braunschweig, sixth, 1930 edition reprinted in [1932] below, vol. 3, pp. 335–390; second, 1893 edition translated in [1963] below, pp. 29–115.Google Scholar
[1932] Dedekind, Richard, Gesammelte mathematische Werke (Fricke, Robert, Noether, Emmy, and Ore, Öystein, editors), F. Vieweg, Baunschweig, reprinted in Chelsea, New York, 1969.Google Scholar
[1963] Dedekind, Richard, Essays on the theory of numbers, Dover, New York, translation by Wooster W. Beman (reprint of original edition, Open Court, Chicago, 1901).Google Scholar
[1997] Dreben, Burton and Kanamori, Akihiro, Hilbert and set theory, Synthese, vol. 110, pp. 77–125.Google Scholar
[1982] Dugundji, James and Granas, Andrzej, Fixed point theory, Państwowe Wydawnictwo, Naukowe, Warsaw.Google Scholar
[1995] Forster, Thomas E., Set theory with a universal set, second ed., Logic Oxford Guides, no. 31, Clarendon Press, Oxford.Google Scholar
[1879] Frege, Gottlob, Begriffsschrift, eine der arithmetischen nachgëbildete Formelsprache des reinen Denkens, Nebert, Halle, reprinted Hildesheim, Olms, 1964; translated in van Heijenoort [1967], pp. 1–82.Google Scholar
[1893] Frege, Gottlob, Grundgesetze der Arithmetik, Begriffsschriftlich abgeleitet, vol. 1, Hermann Pohle, Jena, reprinted Olms, Hildesheim, 1962.Google Scholar
[1895] Frege, Gottlob, Kritische Beleuchtung einiger Punkte in E. Schröders Vorlesungen über die Algebra der Logik, Archiv für systematische Philosophie, vol. 1, pp. 433–456, translated in [1952] below, pp. 86–106.Google Scholar
[1952] Frege, Gottlob, Translations from the Philosophical Writings of Gottlob Frege, Geach, Peter and Black, Max (translators and editors), Blackwell, Oxford, second, revised edition 1960; latest edition, Rowland & Littlewood, Totowa, 1980.Google Scholar
[1992] Garciadiego, Alejandro R., Bertrand Russell and the origins of the set-theoretic “paradoxes”, Birkhäuser, Boston.Google Scholar
[1980] Gierz, Gerhard, Hofmann, Karl H., Keimel, Klaus, Lawson, Jimmie D., Mislove, Michael, and Scott, Dana S., A compendium of continuous lattices, Springer-Verlag, Berlin.Google Scholar
[1938] Gödel, Kurt F., The consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis, Proceedings of the National Academy of Sciences U.S.A., vol. 24, pp. 556–557, reprinted in [1990] below, pp. 26–27.Google Scholar
[1990] Gödel, Kurt F., Collected works (Feferman, Solomon et al., editors), vol. 2, Oxford University Press, New York.Google Scholar
[1988] Goldfarb, Warren, Poincaré against the logicists, History and philosophy of modern mathematics (Aspray, William and Kitcher, Philip, editors), Minnesota Studies in the Philosophy of Science, vol. 11, University of Minnesota Press, Minneapolis, pp. 61–81.Google Scholar
[1977] Grattan-Guinness, Ivor, Dear Russell—Dear Jourdain, Duckworth & Co., London, and Columbia University Press, New York.Google Scholar
[1978] Grattan-Guinness, Ivor, How Bertrand Russell discovered his paradox, Historia Mathematica, vol. 5, pp. 127–137.Google Scholar
[1994] Gray, Robert, Georg Cantor and transcendental numbers, American Mathematical Monthly, vol. 101, pp. 819–832.CrossRefGoogle Scholar
[1984] Hallett, Michael, Cantorian set theory and limitation of size, Logic Guides, no. 10, Clarendon Press, Oxford.Google Scholar
[1903] Hardy, Godfrey H., A theorem concerning the infinite cardinal numbers, The Quarterly Journal of Pure and Applied Mathematics, vol. 35, pp. 87–94, reprinted in [1979] below, vol. 7, pp. 427–434.Google Scholar
[1979] Hardy, Godfrey H., Collected papers of G. H. Hardy (Busbridge, I. W. and Rankin, R. A., editors), Clarendon, Oxford.Google Scholar
[1915] Hartogs, Friedrich, Über das Problem der Wohlordnung, Mathematische Annalen, vol. 76, pp. 436–443.CrossRefGoogle Scholar
[1909] Hausdorff, Felix, Die Graduierung nach dem Endverlauf, Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematische-Physische Klasse, vol. 61, pp. 297–334.Google Scholar
[1906] Hessenberg, Gerhard, Grundbegriffe der mengenlehre, Vandenhoeck & Ruprecht, Göttingen, reprinted from Abhandlungen der Fries'schen Schule, Neue Folge , vol. 1 (1906), pp. 479–706.Google Scholar
[1909] Hessenberg, Gerhard, Ketten theorie und Wohlordnung, Journal für die reine und angewandte Mathematik (Crelle's Journal), vol. 135, pp. 81–133.Google Scholar
[1891] Husserl, Edmund, Besprechung von E. Schröder, Vorlesungen über die Algebra der Logic (Exakte logik), Göttingische Gelehrte Anzeigen, vol. I, Leipzig 1890, pp. 243–278; reprinted in Edmund Husserl, Aufsätze und Rezensionen (1890–1910) , Husserliana, vol. XXII, Nijhoff, The Hague, 1978, pp. 3–43.Google Scholar
[1990] Hylton, Peter, Russell, idealism, and the emergence ofanalytic philosophy, Clarendon Press, Oxford.Google Scholar
[1904] Jourdain, Philip E. B., On the transfinite cardinal numbers of well-ordered aggregates, Philosophical Magazine, vol. 7, pp. 61–75.Google Scholar
[1905] Jourdain, Philip E. B., On a proof that every aggregate can be well-ordered, Mathematische Annalen, vol. 60, pp. 465–470.CrossRefGoogle Scholar
[1996] Kanamori, Akihiro, The mathematical development of set theory from Cantor to Cohen, this Bulletin, vol. 2, pp. 1–71.Google Scholar
[1938] Kleene, Stephen C., On notation for ordinal numbers, The Journal of Symbolic Logic, vol. 3, pp. 150–155.CrossRefGoogle Scholar
[1952] Kleene, Stephen C., Introduction to metamathematics, Van Nostrand, Princeton.Google Scholar
[1928] Knaster, BronisŁaw, Un théorème sur les fonctions d'ensembles, Annales de la Société Polonaise de Mathématique, vol. 6, pp. 133–134.Google Scholar
[1950] Kneser, Helmuth, Eine direkte Ableitung des Zornschen Lemmas aus dem Auswahlaxiom, Mathematische Zeitschrift, vol. 53, pp. 110–113.Google Scholar
[1921] Kuratowski, Kazimierz, Sur la notion de l'ordre dans la théorie des ensembles, Fundamenta Mathematicae, vol. 2, pp. 161–171.Google Scholar
[1922] Kuratowski, Kazimierz, Une méthode d'élimination des nombres transfinis des raisonnements mathématiques, Fundamenta Mathematicae, vol. 3, pp. 76–108.Google Scholar
[1930] Landau, Edmund, Grundlagen der analysis, Akademische Verlagsgesellschaft, Leipzig, translated as Foundations of analysis , Chelsea, New York, 1951.Google Scholar
[1971] Lang, Serge, Algebra, Addison-Wesley, Reading, revised printing of original 1965 edition.Google Scholar
[1982] Moore, Gregory H., Zermelo's Axiom of Choice. its origins, development and influence, Springer-Verlag, New York.Google Scholar
[1995] Moore, Gregory H., The origins of Russell's paradox: Russell, Couturat, and the antimony of infinite number, From Dedekind to Godel (Hintikka, Jaakko, editor), Synthese Library, vol. 251, Kluwer, Dordrecht, pp. 215–239.Google Scholar
[1981] Moore, Gregory H. and Garciadiego, Alejandro R., Burali-Forti's paradox: A reappraisal of its origins, Historia Mathematica, vol. 8, pp. 319–350.Google Scholar
[1974] Moschovakis, Yiannis N., Elementary induction on abstract structures, North-Holland, Amsterdam.Google Scholar
[1994] Moschovakis, Yiannis N., Notes on set theory, Springer-Verlag, New York.Google Scholar
[1937] Noether, Emmy and Cavaillès, Jean (editors), Briefwechsel Cantor-Dedekind, Hermann, Paris.Google Scholar
[1889] Peano, Guiseppe, Arithmetices principia nova methodo exposita, Bocca, Turin, reprinted in [1957–9] below, vol. 2, pp. 20–55; partially translated in van Heijenoort [1967], pp. 85–97; translated in [1973] below, pp. 101–134.Google Scholar
[1890] Peano, Guiseppe, Démonstration de l'intégrabilité des équations différentielles ordinaires, Mathematische Annalen, vol. 37, pp. 182–228, reprinted in [1957] below, vol. 1, pp. 119–170.Google Scholar
[1906] Peano, Guiseppe, Super theorema de Cantor-Bernstein, Rendiconti del Circolo Matematico di Palermo, vol. 21, pp. 360–366, reprinted in [1957–9] below, vol. 1, pp. 337–344.Google Scholar
[1957–1959] Peano, Guiseppe, Opere scelte (Cassina, U., editor), Edizioni Cremonese, Rome, three volumes.Google Scholar
[1973] Peano, Guiseppe, Selected works of Giuseppe Peano (Hubert C. Kennedy, editor), University of Toronto Press, Toronto, translated by Hubert C. Kennedy.Google Scholar
[1990] Peckhaus, Volker, “Ich habe mich wohl gehütet, alle Patronen auf einmal zu verschiessen”. Ernst Zermelo in Göttingen, History and Philosophy of Logic, vol. 11, pp. 19–58.Google Scholar
[1992] Phillips, I. C. C., Recursion theory, Handbook of logic in computer science (Abramsky, S., Gabbay, Dov M., and Maibaum, T. S. E., editors), vol. 1, Clarendon Press, Oxford, pp. 80–187.Google Scholar
[1884] Poincaré, Henri, Sur certaines solutions particulièrs du problème des trois corps, Bulletin Astronomique, vol. 1, pp. 65–74, reprinted in [1952] below, pp. 253–261.Google Scholar
[1905] Poincaré, Henri, Les mathématiques et la logique, Revue de Métaphysique et de Morale, vol. 13, pp. 815–835, also vol. 14 (1906), pp. 17–34.Google Scholar
[1906] Poincaré, Henri, Les mathématiques et la logique, Revue de Métaphysique et de Morale, vol. 14, pp. 294–317.Google Scholar
[1952] Poincaré, Henri, Oeuvres de Henri Poincaré, vol. 7, Gauthier-Villars, Paris.Google Scholar
[1940] Quine, Willard V O., Mathematical logic, Norton, New York.Google Scholar
[1981] Rang, Bernhard and Thomas, Wolfgang, Zermelo's discovery of the “Russell paradox”, Historia Mathematica, vol. 8, pp. 15–22.Google Scholar
[1901] Russell, Bertrand A. W., Recent Italian work on the foundations of mathematics, in [1993] below, pp. 350–362 (page references are to these).Google Scholar
[1901a] Russell, Bertrand A. W., Recent work on the principles of mathematics, International Monthly, vol. 4, pp. 83–101, reprinted as “Mathematics and the Metaphysicians” (with six footnotes added in 1917) in [1918] below, Chapter V, pp. 74–94 (page references are to these); this version reprinted in [1993] below, pp. 363–379.Google Scholar
[1903] Russell, Bertrand A. W., The principles of mathematics, Cambridge University Press, Cambridge, later editions, George Allen & Unwin, London.Google Scholar
[1906] Russell, Bertrand A. W., On some difficulties in the theory of transfinite numbers and order types, Proceedings of the London Mathematical Society, vol. (2)4, pp. 29–53, reprinted in [1973] below, pp. 135–164.Google Scholar
[1906a] Russell, Bertrand A. W., Les paradoxes de la logique, Revue de Métaphysique et de Morale, vol. 14, pp. 627–650, translated in [1973] below, pp. 190–214.Google Scholar
[1908] Russell, Bertrand A. W., Mathematical logic as based on the theory of types, American Journal of Mathematics, vol. 30, pp. 222–262, reprinted in van Heijenoort [1967], pp. 150–182.CrossRefGoogle Scholar
[1918] Russell, Bertrand A. W., Mysticism and logic, and other essays, Longmans, Green & Co., New York.Google Scholar
[1944] Russell, Bertrand A. W., My mental development, The philosophy of Bertrand Russell (Schilpp, Paul A., editor), The Library of Living Philosophers, vol. 5, Northwestern University, Evanston, pp. 3–20.Google Scholar
[1959] Russell, Bertrand A. W., My philosophical development, George Allen & Unwin, London.Google Scholar
[1973] Russell, Bertrand A. W., Essays in analysis (Lackey, Douglas, editor), George Braziller, New York.Google Scholar
[1983] Russell, Bertrand A. W., Cambridge essays, 1888–99 (Blackwell, Kenneth et al., editors), The Collected Works of Bertrand Russell, vol. 1, George Allen & Unwin, London.Google Scholar
[1992] Russell, Bertrand A. W., The selected letters of Bertrand Russell, Volume 1: The private years, 1884–1914 (Griffin, Nicholas, editor), Houghton Mifflin, Boston.Google Scholar
[1993] Russell, Bertrand A. W., Toward the “principles of mathematics”, 1900–1902 (Moore, Gregory H., editor), The Collected Works of Bertrand Russell, vol. 3, Routledge, London.Google Scholar
[1890] Schröder, Ernst, Vorlesungen über die Algebra der Logik (exakte Logik), vol. 1, B. G. Teubner, Leipzig, reprinted in [1966] below.Google Scholar
[1966] Schröder, Ernst, Vorlesungen über die Algebrader Logik, Chelsea, New York, three volumes.Google Scholar
[1962] Scott, Dana S., Quine's individuals, Logic, methodology and the philosophy of science (Nagel, Ernst, editor), Stanford University Press, Stanford, pp. 111–115.Google Scholar
[1975] Scott, Dana S., Data types as lattices, Logic conference, Kiel 1974 (Müller, Gert H., Oberschelp, Arnold, and Potthoff, Klaus, editors), Lecture Notes in Mathematics, no. 499, Springer-Verlag, Berlin, pp. 579–651.Google Scholar
[1971] Sinaceur, Mohammed A., Appartenance et inclusion: un inedit de Richard Dedekind, Revue d'Histoire des Sciences et de leurs Applications, vol. 24, pp. 247–255.Google Scholar
[1957] Specker, Ernst, Zur Axiomatik der Mengenlehre (Fundierungs- und Auswahlaxiom), Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 3, pp. 173–210.Google Scholar
[1977] Stoy, Joseph E., Denotational semantics. The Scott-Strachey approach to programming language theory, MIT Press, Cambridge, third printing, 1985.Google Scholar
[1949–1950] Szele, T., On Zorn's lemma, Publicationes Mathematicae Debrecen, vol. 1, pp. 254–256, cf. Errata, p. 257.Google Scholar
[1939] Tarski, Alfred, On well-ordered subsets of any set, Fundamenta Mathematicae, vol. 32, pp. 176–183.Google Scholar
[1955] Tarski, Alfred, A lattice-theoretical fixpoint theorem and its applications, Pacific Journal of Mathematics, vol. 5, pp. 285–309.Google Scholar
[1966] van der Waerden, Bartel L., Algebra I, seventh ed., Springer-Verlag, Berlin, translated into English, Ungar, New York 1970; this translation reprinted by Springer-Verlag, Berlin 1991.Google Scholar
[1967] van Heijenoort, Jean (editor), From Frege to Gödel: A source book in mathematical logic, 1879–1931, Harvard University Press, Cambridge.Google Scholar
[1923] von Neumann, John, Zur Einführung der transfiniten Zahlen, Acta Litterarum ac Scientiarum Regiae Universitatis Hungaricae Francisco-Josephinae, sectio scientiarum mathematicarum, vol. 1, pp. 199–208, reprinted in [1961] below, pp. 24–33; translated in van Heijenoort [1967], pp. 346–354.Google Scholar
[1925] von Neumann, John, Eine Axiomatisierung der Mengenlehre, Journal für die reine und angewandte Mathematik (Crelle's Journal), vol. 154, pp. 219–240, Berichtigung, vol 155, p. 128; reprinted in [1961] below, pp. 34–56; translated in van Heijenoort [1967], pp. 393–413.Google Scholar
[1928] von Neumann, John, Über die Definition durch transfinite Induktion und verwandte Fragen der allgemeinen Mengenlehre, Mathematische Annalen, vol. 99, pp. 373–391, reprinted in [1961] below, pp. 320–338.Google Scholar
[1961] von Neumann, John, John von Neumann. Collected works (Taub, Abraham H., editor), vol. 1, Pergamon Press, New York.Google Scholar
[1954] Weston, Jeffrey D., A short proof of Zorn's lemma, Archiv der Mathematik, vol. 8, p. 279.Google Scholar
[1910–1913] Whitehead, Alfred N. and Russell, Bertrand A. W., Principia mathematica, Cambridge University Press, Cambridge, three volumes.Google Scholar
[1904] Zermelo, Ernst, Beweis, dass jede Menge wohlgeordnet werden kann (Aus einem an Herrn Hilbert gerichteten Briefe), Mathematische Annalen, vol. 59, pp. 514–516, translated in van Heijenoort [1967], pp. 139–141.Google Scholar
[1908] Zermelo, Ernst, Neuer Beweis für die Möglichkeit einer Wohlordnung, Mathematische Annalen, vol. 65, pp. 107–128, translated in van Heijenoort [1967], pp. 183–198.Google Scholar
[1908a] Zermelo, Ernst, Untersuchungen über die Grundlagen der Mengenlehre I, Mathematische Annalen, vol. 65, pp. 261–281, translated in van Heijenoort [1967], pp. 199–215.Google Scholar
[1935] Zorn, Max, A remark on method in transfinite algebra, Bulletin of the American Mathematical Society, vol. 41, pp. 667–670.Google Scholar