Many problems, different frameworks: classification of problems in computable analysis and algorithmic learning theory

Abstract

In this thesis, we study the complexity of some mathematical problems: in particular, those arising in computable analysis and algorithmic learning theory for algebraic structures. Our study is not limited to these two areas: indeed, in both cases, the results we obtain are tightly connected to ideas and tools coming from different areas of mathematical logic, including for example descriptive set theory and reverse mathematics.

After giving the necessary preliminaries, we first study the uniform computational strength of the Cantor–Bendixson theorem in the Weihrauch lattice. This work falls into the program connecting reverse mathematics and computable analysis via the framework of Weihrauch reducibility. We concentrate on problems related to perfect subsets of Polish spaces, studying the perfect set theorem, the Cantor–Bendixson theorem, and various problems arising from them. As far as we know, this is the first systematic study of problems at the level of 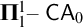$\mathbf {\Pi }^1_1\mathsf {-CA}_0$ in the Weihrauch lattice. We show that the strength of some of the problems we study depends on the topological properties of the Polish space under consideration, while others have the same strength once the space is rich enough.

We continue considering problems related to (induced) subgraphs. We provide results on the (effective) Wadge complexity of sets of graphs, that are also used to determine the Weihrauch degree of certain decision problems. The decision problems we consider are defined for a fixed graph G, and they take as input a graph H, answering whether G is an (induced) subgraph of H: we also consider the opposite problem (i.e., answering whether H is an induced subgraph of G). We conclude this part on (induced) subgraphs considering the Weihrauch degree of “search problems.”These problems are defined for a fixed graph G, and they take as input a graph H such that G is an (induced) subgraph H: the output is a copy of G in H. In both cases, we highlight differences and analogies between the subgraph and the induced subgraph relation.

We then move our attention to algorithmic learning theory, and we present the framework we use to study the learnability of families of algebraic structures: here, given a countable family of pairwise nonisomorphic structures 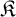$\mathfrak {K}$, a learner receives larger and larger pieces of an arbitrary copy of a structure in 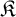$\mathfrak {K}$ and, at each stage, is required to output a conjecture about the isomorphism type of such a structure. We say that 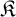$\mathfrak {K}$ is learnable if there exists a learner which eventually stabilizes to a correct guess. The framework was lacking a method for comparing the complexity of nonlearnable families, and so we propose a solution to this problem using tools coming from invariant descriptive set theory. To do so, we first prove that a family of structures is learnable if and only if its learning domain is continuously reducible to the relation 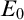$E_0$ of eventual agreement on infinite binary sequences and then, replacing 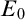$E_0$ with Borel equivalence relations of higher complexity, we obtain a new hierarchy of learning problems. This leads to the notion of E-learnability, where a family of structures 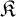$\mathfrak {K}$ is E-learnable, for a Borel equivalence relation E, if there is a continuous reduction from the isomorphism relation associated with 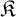$\mathfrak {K}$ to E. It is then natural to ask how the notion of E-learnability interacts with “classical” learning paradigms.

Finally, we study the number of mind changes that a learner needs to learn a given family, both from a topological and a combinatorial point of view, and we consider how the complexity of a learner (in terms of Turing reducibility) affects the number of mind changes for learning a given family.

Abstract prepared by Vittorio Cipriani.

E-mail: [email protected].

URL: https://air.uniud.it/handle/11390/1252226.