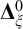1 Introduction
Ever since Mostowski [Reference Mostowski45] and Addison [Reference Addison1] observed the connections between Kleene’s work on computability and the hyperarithmetic hierarchy [Reference Kleene24, Reference Kleene25] and Lusin and Souslin’s study of Borel and analytic sets [Reference Lusin38, Reference Suslin56], effective methods have been widely used in descriptive set theory. The computable theory gives alternative proofs of classical arguments, for example, Addison’s proof of Kondo’s co-analytic uniformisation [Reference Kondo29], Sacks’ proof of the measurability of analytic sets (see [Reference Sacks49, Lemma II.6.2]), or Solovay’s effectivised Galvin–Prikry theorem [Reference Solovay54]. More recently, effective tools were used for the
![]() $E_0$
-dichotomy for Borel equivalence relations [Reference Harrington, Kechris and Louveau19] and the
$E_0$
-dichotomy for Borel equivalence relations [Reference Harrington, Kechris and Louveau19] and the
![]() $G_0$
-dichotomy for Borel graph colourings [Reference Kechris, Solecki and Todorčević23]. Perhaps the most prominent interaction of the effective and classical hierarchies appears in Louveau’s separation theorem [Reference Louveau35], and other work of Loueveau, Saint Raymond, and Debs [Reference Debs9, Reference Louveau and Saint Raymond36, Reference Louveau and Saint Raymond37].
$G_0$
-dichotomy for Borel graph colourings [Reference Kechris, Solecki and Todorčević23]. Perhaps the most prominent interaction of the effective and classical hierarchies appears in Louveau’s separation theorem [Reference Louveau35], and other work of Loueveau, Saint Raymond, and Debs [Reference Debs9, Reference Louveau and Saint Raymond36, Reference Louveau and Saint Raymond37].
Beyond the basic understanding of the hyperarithmetic hierarchy as a refinement of the Borel one, a number of tools involving computability theory have been used in these studies, for instance, computability on admissible sets, and the Gandy–Harrington topology. However, the most unique and central technique of computability, the priority method initiated by Friedberg [Reference Friedberg14] and Muchnik [Reference Mučnik46], appeared to have limited application to questions of set theory. Martin’s original proof of Borel determinacy [Reference Martin41] had a finite-injury aspect to it; recent work by Lecomte and Zeleny [Reference Lecomte and Zeleny32] involves an infinite-injury argument.
The priority method was used recently, in work of Day, Downey, and Westrick studying topological degrees of discontinuous functions [Reference Day, Downey and Westrick7], and then in Day and Marks’s resolution of the decomposability conjecture [Reference Day and Marks6]. Both of these used iterated priority arguments, in particular, as formulated by Montalbán’s true stages machinery.
Iterated priority arguments originated in works of Harrington (unpublished; see [Reference Knight27, Reference Knight28]) and Ash [Reference Ash2] (see [Reference Ash and Knight4]) in computable structure theory. These are complex priority arguments whose iterated nature reflects the hyperarithmetic hierarchy. They are used to construct computable objects while satisfying some ordinal-height system of requirements and guessing at non-computable information. The idea is to break such a construction down into smaller, more tractable pieces. A typical application is the Ash–Watnick theorem [Reference Ash3], which states that if
![]() $\delta $
is a computable ordinal and
$\delta $
is a computable ordinal and
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $\Delta ^0_{2\delta +1}$
linear ordering, then
$\Delta ^0_{2\delta +1}$
linear ordering, then
![]() $\mathbb Z^\delta \cdot \mathcal {L}$
has a computable copy. Here we guess at what
$\mathbb Z^\delta \cdot \mathcal {L}$
has a computable copy. Here we guess at what
![]() $\mathcal {L}$
is, while building approximations to an iteration (of length
$\mathcal {L}$
is, while building approximations to an iteration (of length
![]() $\delta $
) of the Hausdorff derivative of our copy of
$\delta $
) of the Hausdorff derivative of our copy of
![]() $\mathbb Z^\delta \cdot \mathcal {L}$
. Another style of iterated priority arguments has been formulated by Lempp and Lerman [Reference Lempp and Lerman33, Reference Lerman34], who use sequences of trees of strategies to unfold complicated requirements.
$\mathbb Z^\delta \cdot \mathcal {L}$
. Another style of iterated priority arguments has been formulated by Lempp and Lerman [Reference Lempp and Lerman33, Reference Lerman34], who use sequences of trees of strategies to unfold complicated requirements.
Montalbán [Reference Montalbán43] extended Ash’s metatheorem and presented it in a dynamic way, using the concept of true stages. This concept generalises Dekker’s non-deficiency stages, those which provide a correct approximation of the halting problem. Perhaps surprisingly, using a relativised version, true stages turn out to also be of use in constructing functions on Baire space and other Polish spaces, as was demonstrated by Day, Downey, and Westrick, and Day and Marks. In some sense, however, the history of such applications goes back several decades: Louveau and Saint Raymond developed a technique called the ramification method to prove Borel Wadge determinacy [Reference Louveau and Saint Raymond36, Reference Louveau and Saint Raymond37]. An examination of this technique reveals that it is fundamentally a “worker argument,” Harrington’s formulation of his iterated priority arguments. More recently, Debs and Saint Raymond’s representation theorem for Borel sets [Reference Debs and Raymond10] uses an iterated unravelling of sets based on finite approximations, and has some features which resemble Montalbán’s method. Our approach differs from theirs in our focus on dynamic processes in set definitions.
The purpose of this paper is to describe the general true stages machinery and illustrate its applications to descriptive set theory by providing new proofs of several results. We start with results which do not actually require a priority argument, but for which the machinery gives smooth proofs regardless: we discuss changes of topology, the Hausdorff–Kuratowski theorem on the structure of
![]() $\mathbf {\Delta }^0_{\xi +1}$
, and Wadge’s theorem on the structure of
$\mathbf {\Delta }^0_{\xi +1}$
, and Wadge’s theorem on the structure of
![]() $\mathbf {\Delta }^0_{\lambda }$
, for
$\mathbf {\Delta }^0_{\lambda }$
, for
![]() $\lambda $
limit. We then show how to use true stages for a priority argument, and give a proof of Louveau’s separation theorem.
$\lambda $
limit. We then show how to use true stages for a priority argument, and give a proof of Louveau’s separation theorem.
These studies have applications to reverse mathematics. The question of the axiomatic strength of results in descriptive set theory was raised by Louveau and Saint Raymond. In [Reference Louveau and Saint Raymond37] they showed that Borel Wadge determinacy is provable in second-order arithmetic. This was quite surprising, since the most straightforward proof relies on Borel determinacy, which is known to require strong axioms [Reference Friedman15], and since
![]() $\boldsymbol {\Pi }^1_1$
Wadge determinacy was known to be equivalent to full
$\boldsymbol {\Pi }^1_1$
Wadge determinacy was known to be equivalent to full
![]() $\boldsymbol {\Pi }^1_1$
determinacy [Reference Harrington18], the same holds for
$\boldsymbol {\Pi }^1_1$
determinacy [Reference Harrington18], the same holds for
![]() $\boldsymbol {\Pi }^1_2$
[Reference Hjorth21]. The ramification method allowed Louveau and Saint Raymond to avoid the reliance on Borel determinacy and rather reduce the Borel Wadge games to closed games. Similarly, the standard proof of Louveau’s separation theorem uses the Gandy–Harrington topology, and can be carried out using the
$\boldsymbol {\Pi }^1_2$
[Reference Hjorth21]. The ramification method allowed Louveau and Saint Raymond to avoid the reliance on Borel determinacy and rather reduce the Borel Wadge games to closed games. Similarly, the standard proof of Louveau’s separation theorem uses the Gandy–Harrington topology, and can be carried out using the
![]() $\Pi ^1_1$
-comprehension axiom system. Our proof shows that in fact, the weaker system
$\Pi ^1_1$
-comprehension axiom system. Our proof shows that in fact, the weaker system
![]() $\mathsf {ATR}_0$
(arithmetical transfinite recursion) suffices.
$\mathsf {ATR}_0$
(arithmetical transfinite recursion) suffices.
This paper is intended as one of a pair. In the companion paper [Reference Day, Greenberg, Harrison-Trainor and Turetsky8], we give a new and effective classification of all Borel Wadge classes, using the true stages machinery. A corollary is a proof of Borel Wadge determinacy in
![]() $\mathsf {ATR}_0 + \Sigma ^1_1$
-
$\mathsf {ATR}_0 + \Sigma ^1_1$
-
![]() $\mathsf {IND}$
. One of the steps is a proof of the Louveau and Saint Raymond separation theorem [Reference Louveau and Saint Raymond36] for all Borel Wadge classes. In the current paper we give the simpler argument, for the classes
$\mathsf {IND}$
. One of the steps is a proof of the Louveau and Saint Raymond separation theorem [Reference Louveau and Saint Raymond36] for all Borel Wadge classes. In the current paper we give the simpler argument, for the classes
![]() $\boldsymbol {\Sigma }^0_\xi $
, from which we derive the Louveau separation theorem.
$\boldsymbol {\Sigma }^0_\xi $
, from which we derive the Louveau separation theorem.
1.1 A note on subscripts
In the hyperarithmetic hierarchy, statements about the finite levels of the hierarchy often have an “off by one” error when generalized to the infinite levels. This is illustrated by (and can be viewed as originating from) the following pair of results:
Proposition 1.1 (Post [Reference Post48]).
For
![]() $n < \omega $
and a set
$n < \omega $
and a set
![]() $X \subseteq \omega $
,
$X \subseteq \omega $
,
![]() $X \leqslant _T \emptyset ^{(n)}$
if and only if
$X \leqslant _T \emptyset ^{(n)}$
if and only if
![]() $X \in \Delta ^0_{n+1}$
.
$X \in \Delta ^0_{n+1}$
.
Proposition 1.2 (Ash; see [Reference Ash and Knight4]).
For
![]() $\omega \leqslant \alpha < \omega _1^{\text {ck}}$
and a set
$\omega \leqslant \alpha < \omega _1^{\text {ck}}$
and a set
![]() $X \subseteq \omega $
,
$X \subseteq \omega $
,
![]() $X \leqslant _T \emptyset ^{(\alpha )}$
if and only if
$X \leqslant _T \emptyset ^{(\alpha )}$
if and only if
![]() $X \in \Delta ^0_\alpha $
.
$X \in \Delta ^0_\alpha $
.
Observe that the subscript in the first result contains “
![]() $+1$
,” while the subscript in the second does not. Ultimately, this comes down to the fact that computable corresponds to
$+1$
,” while the subscript in the second does not. Ultimately, this comes down to the fact that computable corresponds to
![]() $\Delta ^0_1$
rather than
$\Delta ^0_1$
rather than
![]() $\Delta ^0_0$
. Similarly, the class of open sets is denoted
$\Delta ^0_0$
. Similarly, the class of open sets is denoted
![]() $\boldsymbol {\Sigma }^0_1$
rather than
$\boldsymbol {\Sigma }^0_1$
rather than
![]() $\boldsymbol {\Sigma }^0_0$
, which contrasts, for example, with the Baire hierarchy of Borel functions. This can be unified, however, by making use of
$\boldsymbol {\Sigma }^0_0$
, which contrasts, for example, with the Baire hierarchy of Borel functions. This can be unified, however, by making use of
![]() $1+\alpha $
. Note that for
$1+\alpha $
. Note that for
![]() $\alpha < \omega $
,
$\alpha < \omega $
,
![]() $1+\alpha = \alpha +1$
, while for
$1+\alpha = \alpha +1$
, while for
![]() $\alpha \geqslant \omega $
,
$\alpha \geqslant \omega $
,
![]() $1+\alpha = \alpha $
. Thus the following holds:
$1+\alpha = \alpha $
. Thus the following holds:
Proposition 1.3. For
![]() $\alpha < \omega _1^{\text {ck}}$
and a set
$\alpha < \omega _1^{\text {ck}}$
and a set
![]() $X \subseteq \omega $
,
$X \subseteq \omega $
,
![]() $X \leqslant _T \emptyset ^{(\alpha )}$
if and only if
$X \leqslant _T \emptyset ^{(\alpha )}$
if and only if
![]() $X \in \Delta ^0_{1+\alpha }$
.
$X \in \Delta ^0_{1+\alpha }$
.
We will make extensive use of this device, generally in the subscripts of
![]() $\Delta $
’s and
$\Delta $
’s and
![]() $\Sigma $
’s.
$\Sigma $
’s.
2 Change of topology and true stages
A commonly used technique in descriptive set theory is the enrichment of the topology of a Polish space. For simplicity, we shall restrict ourselves in this paper to Baire space
![]() $\mathcal {N} = \omega ^\omega $
. The following is a version of [Reference Kechris22, Theorem 13.1]:
$\mathcal {N} = \omega ^\omega $
. The following is a version of [Reference Kechris22, Theorem 13.1]:
Proposition 2.1. If
![]() $A\subseteq \mathcal {N}$
is Borel, then there is a Polish topology on
$A\subseteq \mathcal {N}$
is Borel, then there is a Polish topology on
![]() $\mathcal {N}$
, extending the standard one, and which has the same Borel sets, in which A is open.
$\mathcal {N}$
, extending the standard one, and which has the same Borel sets, in which A is open.
The proof given in [Reference Kechris22] is direct, by induction on the Borel rank of A. Alternatively, it can be deduced from a characterisation of classes of Borel sets in terms of generalised homeomorphisms, due to Kuratowski [Reference Kuratowski30] and Sierpiński [Reference Sierpiński52]. Recall that a function
![]() $f\colon Y\to X$
between Polish spaces is
$f\colon Y\to X$
between Polish spaces is
![]() $\boldsymbol {\Sigma }^0_\xi $
-measurable if
$\boldsymbol {\Sigma }^0_\xi $
-measurable if
![]() $f^{-1}[U]$
is
$f^{-1}[U]$
is
![]() $\boldsymbol {\Sigma }^0_\xi $
for every open set
$\boldsymbol {\Sigma }^0_\xi $
for every open set
![]() $U\subseteq X$
. A function
$U\subseteq X$
. A function
![]() $f\colon \mathcal {N}\to X$
is
$f\colon \mathcal {N}\to X$
is
![]() $\boldsymbol {\Sigma }^0_{\xi +1}$
-measurable if and only if it is Baire class
$\boldsymbol {\Sigma }^0_{\xi +1}$
-measurable if and only if it is Baire class
![]() $\xi $
(see [Reference Kechris22, Theorem 24.3]). Kuratowski and Sierpiński essentially showed:
$\xi $
(see [Reference Kechris22, Theorem 24.3]). Kuratowski and Sierpiński essentially showed:
Proposition 2.2. Let
![]() $\xi \geqslant 1$
. A set
$\xi \geqslant 1$
. A set
![]() $A\subseteq \mathcal {N}$
is
$A\subseteq \mathcal {N}$
is
![]() $\boldsymbol {\Sigma }^0_{\xi }$
if and only if there is a closed set
$\boldsymbol {\Sigma }^0_{\xi }$
if and only if there is a closed set
![]() $E\subseteq \mathcal {N}$
and a bijection
$E\subseteq \mathcal {N}$
and a bijection
![]() $f\colon \mathcal {N}\to E$
such that:
$f\colon \mathcal {N}\to E$
such that:
-
(i) f is
 $\boldsymbol {\Sigma }^0_\xi $
-measurable;
$\boldsymbol {\Sigma }^0_\xi $
-measurable; -
(ii)
 $f^{-1}$
is continuous; and
$f^{-1}$
is continuous; and -
(iii)
 $A = f^{-1}[B]$
for some open
$A = f^{-1}[B]$
for some open
 $B\subseteq \mathcal {N}$
.
$B\subseteq \mathcal {N}$
.
For a detailed account, see [Reference Wadge57, Theorem IV.C.10]. Proposition 2.1 can be directly deduced from Proposition 2.2 by taking the topology on
![]() $\mathcal {N}$
which makes f a homeomorphism between
$\mathcal {N}$
which makes f a homeomorphism between
![]() $\mathcal {N}$
and E; we know that a closed subset of
$\mathcal {N}$
and E; we know that a closed subset of
![]() $\mathcal {N}$
is Polish.
$\mathcal {N}$
is Polish.
An effective proof of Proposition 2.2 was observed by A. Marks. For any
![]() $x\in \mathcal {N}$
and ordinal
$x\in \mathcal {N}$
and ordinal
![]() $\alpha <\omega _1^x$
(i.e., x computes a copy of
$\alpha <\omega _1^x$
(i.e., x computes a copy of
![]() $\alpha $
), we let
$\alpha $
), we let
![]() $x^{(\alpha )}$
denote the iteration of the Turing jump operator (the relativised halting problem) along
$x^{(\alpha )}$
denote the iteration of the Turing jump operator (the relativised halting problem) along
![]() $\alpha $
, starting with x. Spector [Reference Spector55] showed that the Turing degree of
$\alpha $
, starting with x. Spector [Reference Spector55] showed that the Turing degree of
![]() $x^{(\alpha )}$
does not depend on the presentation of
$x^{(\alpha )}$
does not depend on the presentation of
![]() $\alpha $
as an x-computable well-ordering. The degree of
$\alpha $
as an x-computable well-ordering. The degree of
![]() $x^{(\alpha )}$
is Turing complete for the
$x^{(\alpha )}$
is Turing complete for the
![]() $\Delta ^0_{1+\alpha }(x)$
sets. Under standard definitions,
$\Delta ^0_{1+\alpha }(x)$
sets. Under standard definitions,
![]() $\{ x^{(\alpha )}\,:\, x\in \mathcal {N} \}$
is a
$\{ x^{(\alpha )}\,:\, x\in \mathcal {N} \}$
is a
![]() $\Pi ^0_2$
subset of Cantor space. It can, however, be pulled back to a
$\Pi ^0_2$
subset of Cantor space. It can, however, be pulled back to a
![]() $\Pi ^0_1$
subset of Baire space: for each x,
$\Pi ^0_1$
subset of Baire space: for each x,
![]() $x^{(\alpha )}$
is a
$x^{(\alpha )}$
is a
![]() $\Pi ^0_2(x)$
singleton, and each
$\Pi ^0_2(x)$
singleton, and each
![]() $\Pi ^0_2(x)$
singleton in Cantor space is Turing equivalent to a
$\Pi ^0_2(x)$
singleton in Cantor space is Turing equivalent to a
![]() $\Pi ^0_1(x)$
singleton in Baire space. This is all uniform in x. After this renaming, the function
$\Pi ^0_1(x)$
singleton in Baire space. This is all uniform in x. After this renaming, the function
![]() $x\mapsto x^{(\alpha )}$
is
$x\mapsto x^{(\alpha )}$
is
![]() $\boldsymbol {\Sigma }^0_{1+\alpha }$
-measurable with closed image and continuous inverse, and the following holds:
$\boldsymbol {\Sigma }^0_{1+\alpha }$
-measurable with closed image and continuous inverse, and the following holds:
Proposition 2.3. Let
![]() $\alpha <\omega _1^{\text {ck}}$
. A set
$\alpha <\omega _1^{\text {ck}}$
. A set
![]() $A\subseteq \mathcal {N}$
is
$A\subseteq \mathcal {N}$
is
![]() $\Sigma ^0_{1+\alpha }$
if and only if there is a
$\Sigma ^0_{1+\alpha }$
if and only if there is a
![]() $\Sigma ^0_1$
set
$\Sigma ^0_1$
set
![]() $V\subseteq \mathcal {N}$
such that
$V\subseteq \mathcal {N}$
such that
![]() $A = \{ x \,:\, x^{(\alpha )}\in V \}$
.
$A = \{ x \,:\, x^{(\alpha )}\in V \}$
.
The relativised jump functions
![]() $x\mapsto (x,z)^{(\alpha )}$
are universal: a function
$x\mapsto (x,z)^{(\alpha )}$
are universal: a function
![]() $f\colon \mathcal {N}\to X$
is
$f\colon \mathcal {N}\to X$
is
![]() $\boldsymbol {\Sigma }^0_{1+\alpha }$
-measurable if and only if there is some oracle (parameter) z and some continuous function
$\boldsymbol {\Sigma }^0_{1+\alpha }$
-measurable if and only if there is some oracle (parameter) z and some continuous function
![]() $g\colon \mathcal {N}\to X$
such that
$g\colon \mathcal {N}\to X$
such that
![]() $f(x) = g((x,z)^{(\alpha )})$
. Thus, Proposition 2.2 can be deduced from its effective version Proposition 2.3. We can also deduce an effective version of Proposition 2.1. For every oracle z and every
$f(x) = g((x,z)^{(\alpha )})$
. Thus, Proposition 2.2 can be deduced from its effective version Proposition 2.3. We can also deduce an effective version of Proposition 2.1. For every oracle z and every
![]() $\alpha < \omega _1^z$
, let the
$\alpha < \omega _1^z$
, let the
![]() $(z,\alpha )$
-topology on
$(z,\alpha )$
-topology on
![]() $\mathcal {N}$
be the topology generated by the
$\mathcal {N}$
be the topology generated by the
![]() $\Sigma ^0_{1+\alpha }(z)$
sets. It extends the standard topology on
$\Sigma ^0_{1+\alpha }(z)$
sets. It extends the standard topology on
![]() $\mathcal {N}$
, and has the same Borel sets. Proposition 2.3 implies the following, which in turn implies Proposition 2.1:
$\mathcal {N}$
, and has the same Borel sets. Proposition 2.3 implies the following, which in turn implies Proposition 2.1:
Proposition 2.4. For every z and every
![]() $\alpha < \omega _1^z$
, the
$\alpha < \omega _1^z$
, the
![]() $(z,\alpha )$
-topology is Polish.
$(z,\alpha )$
-topology is Polish.
2.1 Enter true stages
Baire space is the set of infinite paths through the tree
![]() $(\omega ^{<\omega },\preceq )$
. A metric witnessing that
$(\omega ^{<\omega },\preceq )$
. A metric witnessing that
![]() $\mathcal {N}$
is Polish is derived from the tree:
$\mathcal {N}$
is Polish is derived from the tree:
![]() $d(x,y) = 2^{-|\sigma |}$
, where
$d(x,y) = 2^{-|\sigma |}$
, where
![]() $\sigma $
is the greatest common initial segment of x and y on the tree. Our first application of the true stages machinery will be an extension of this idea to the
$\sigma $
is the greatest common initial segment of x and y on the tree. Our first application of the true stages machinery will be an extension of this idea to the
![]() $(z,\alpha )$
-topology in an internally coherent fashion. For simplicity of notation, we state the unrelativised version (
$(z,\alpha )$
-topology in an internally coherent fashion. For simplicity of notation, we state the unrelativised version (
![]() $z = \emptyset $
).
$z = \emptyset $
).
The true stages machinery provides, for each computable ordinal
![]() $\alpha < \omega _1^{\text {ck}}$
, a partial ordering
$\alpha < \omega _1^{\text {ck}}$
, a partial ordering
![]() $\preceq _\alpha $
on
$\preceq _\alpha $
on
![]() $\omega ^{\leqslant \omega }$
with a variety of useful properties. We will list the properties that we will need as they become relevant. We start with the following four.
$\omega ^{\leqslant \omega }$
with a variety of useful properties. We will list the properties that we will need as they become relevant. We start with the following four.
-
TSP(1): For
 $\sigma ,\tau \in \omega ^{\leqslant \omega }$
,
$\sigma ,\tau \in \omega ^{\leqslant \omega }$
,
 $\sigma \preceq _\alpha \tau $
implies
$\sigma \preceq _\alpha \tau $
implies
 $\sigma \preceq \tau $
. For
$\sigma \preceq \tau $
. For
 $\alpha =0$
,
$\alpha =0$
,
 $\sigma \preceq _0 \tau \,\,\Longleftrightarrow \,\, \sigma \preceq \tau $
.
$\sigma \preceq _0 \tau \,\,\Longleftrightarrow \,\, \sigma \preceq \tau $
. -
TSP(2):
 $(\omega ^{\leqslant \omega }, \preceq _\alpha )$
is a tree: for all
$(\omega ^{\leqslant \omega }, \preceq _\alpha )$
is a tree: for all
 $\tau \in \omega ^{\leqslant \omega }$
,
$\tau \in \omega ^{\leqslant \omega }$
,
 $\left \{ \sigma \,:\, \sigma \preceq _\alpha \tau \right \}$
is linearly ordered; the root of the tree is
$\left \{ \sigma \,:\, \sigma \preceq _\alpha \tau \right \}$
is linearly ordered; the root of the tree is
 ${\left \langle {}\right \rangle }$
(the empty sequence).
${\left \langle {}\right \rangle }$
(the empty sequence). -
TSP(3): For every
 $x\in \mathcal {N}$
,
$x\in \mathcal {N}$
,
 $\left \{ \sigma \in \omega ^{<\omega } \,:\, \sigma \prec _\alpha x \right \}$
is the unique infinite path of the restriction of
$\left \{ \sigma \in \omega ^{<\omega } \,:\, \sigma \prec _\alpha x \right \}$
is the unique infinite path of the restriction of
 $\preceq _\alpha $
to
$\preceq _\alpha $
to
 $\left \{ \sigma \in \omega ^{<\omega } \,:\, \sigma \prec x \right \}$
.
$\left \{ \sigma \in \omega ^{<\omega } \,:\, \sigma \prec x \right \}$
. -
TSP(4): A set
 $A\subseteq \mathcal {N}$
is
$A\subseteq \mathcal {N}$
is
 $\Sigma ^0_{1+\alpha }$
if and only if there is a c.e. set
$\Sigma ^0_{1+\alpha }$
if and only if there is a c.e. set
 $U\subseteq \omega ^{<\omega }$
such that
$U\subseteq \omega ^{<\omega }$
such that  $$\begin{align*}A = [U]^{\prec}_{\alpha} = \left\{ x\in \mathcal{N} \,:\, (\exists \sigma\in U)\,\,\sigma\prec_\alpha x \right\}\!. \end{align*}$$
$$\begin{align*}A = [U]^{\prec}_{\alpha} = \left\{ x\in \mathcal{N} \,:\, (\exists \sigma\in U)\,\,\sigma\prec_\alpha x \right\}\!. \end{align*}$$
Proposition 2.4 for
![]() $z=\emptyset $
follows: we let
$z=\emptyset $
follows: we let
![]() $d_\alpha (x,y) = 2^{-|\sigma |}$
, where
$d_\alpha (x,y) = 2^{-|\sigma |}$
, where
![]() $\sigma $
is the longest string satisfying
$\sigma $
is the longest string satisfying
![]() $\sigma \prec _\alpha x, y$
. The open sets of the
$\sigma \prec _\alpha x, y$
. The open sets of the
![]() $(\emptyset ,\alpha )$
-topology are precisely the sets
$(\emptyset ,\alpha )$
-topology are precisely the sets
![]() $[U]^\prec _\alpha $
for any
$[U]^\prec _\alpha $
for any
![]() $U\subseteq \omega ^{<\omega }$
. TSP(1) implies that this generalises the usual topology. In general, for each oracle z, we can relativise the machinery to z and obtain, for each
$U\subseteq \omega ^{<\omega }$
. TSP(1) implies that this generalises the usual topology. In general, for each oracle z, we can relativise the machinery to z and obtain, for each
![]() $\alpha < \omega _1^z$
, a partial ordering
$\alpha < \omega _1^z$
, a partial ordering
![]() $\preceq ^z_\alpha $
with the same properties, except that in TSP(4) we replace c.e. by z-c.e. and
$\preceq ^z_\alpha $
with the same properties, except that in TSP(4) we replace c.e. by z-c.e. and
![]() $\Sigma ^0_{1+\alpha }$
by
$\Sigma ^0_{1+\alpha }$
by
![]() $\Sigma ^0_{1+\alpha }(z)$
.
$\Sigma ^0_{1+\alpha }(z)$
.
As this is an expository paper, we will relegate to the companion paper [Reference Day, Greenberg, Harrison-Trainor and Turetsky8] the details of the construction of these partial orderings and the verification of their properties. Montalbán first developed his true stages machinery in [Reference Montalbán43], based on his work with Marcone in [Reference Marcone and Montalbán40] on the Veblen functions and the iterated Turing jump. Greenberg and Turetsky then gave an alternative development in [Reference Greenberg and Turetsky16]. Both of these were restricted to
![]() $x = 0^\infty $
. Day, Downey, and Westrick, and Greenberg and Turetsky independently observed that both of these versions can be extended to all of Baire space.
$x = 0^\infty $
. Day, Downey, and Westrick, and Greenberg and Turetsky independently observed that both of these versions can be extended to all of Baire space.
Let us informally describe the main ideas. The relations
![]() $\preceq _\alpha $
are defined by recursion on
$\preceq _\alpha $
are defined by recursion on
![]() $\alpha $
: we first need to define
$\alpha $
: we first need to define
![]() $\preceq _\beta $
for all
$\preceq _\beta $
for all
![]() $\beta <\alpha $
. To make the construction work, these relations need to be internally coherent, for example, they are nested and continuous:
$\beta <\alpha $
. To make the construction work, these relations need to be internally coherent, for example, they are nested and continuous:
-
TSP(5): If
 $\alpha \leqslant \beta $
, then
$\alpha \leqslant \beta $
, then
 $\sigma \preceq _\beta \tau $
implies
$\sigma \preceq _\beta \tau $
implies
 $\sigma \preceq _\alpha \tau $
.
$\sigma \preceq _\alpha \tau $
. -
TSP(6): If
 $\lambda $
is a limit ordinal, then
$\lambda $
is a limit ordinal, then
 $\sigma \preceq _\lambda \tau $
if and only if for all
$\sigma \preceq _\lambda \tau $
if and only if for all
 $\alpha < \lambda $
,
$\alpha < \lambda $
,
 $\sigma \preceq _\alpha \tau $
.
$\sigma \preceq _\alpha \tau $
.
The idea is to define, for each finite sequence
![]() $\sigma $
, a finite sequence
$\sigma $
, a finite sequence
![]() $\sigma ^{(\alpha )}$
, which is
$\sigma ^{(\alpha )}$
, which is
![]() $\sigma $
’s guess of an initial segment of the
$\sigma $
’s guess of an initial segment of the
![]() $\alpha $
-jump of infinite sequences x extending
$\alpha $
-jump of infinite sequences x extending
![]() $\sigma $
. This guess is independent of the choice of
$\sigma $
. This guess is independent of the choice of
![]() $x\succ \sigma $
. The guess may be correct for some choices of x and incorrect for others. Roughly, we let
$x\succ \sigma $
. The guess may be correct for some choices of x and incorrect for others. Roughly, we let
![]() $\sigma \prec _\alpha x$
if
$\sigma \prec _\alpha x$
if
![]() $\sigma ^{(\alpha )}\prec x^{(\alpha )}$
, i.e., when
$\sigma ^{(\alpha )}\prec x^{(\alpha )}$
, i.e., when
![]() $\sigma $
’s guess is correct for x; we say that such a
$\sigma $
’s guess is correct for x; we say that such a
![]() $\sigma $
is an
$\sigma $
is an
![]() $\alpha $
-true initial segment of x. One of the main ideas, though, is the extension of this relation to a relation between two finite sequences
$\alpha $
-true initial segment of x. One of the main ideas, though, is the extension of this relation to a relation between two finite sequences
![]() $\sigma \preceq \tau $
. Again, the idea is to let
$\sigma \preceq \tau $
. Again, the idea is to let
![]() $\sigma \preceq _\alpha \tau $
if
$\sigma \preceq _\alpha \tau $
if
![]() $\sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
: the guesses of
$\sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
: the guesses of
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
about the
$\tau $
about the
![]() $\alpha $
-jump do not contradict each other. We say that
$\alpha $
-jump do not contradict each other. We say that
![]() $\sigma $
appears to be
$\sigma $
appears to be
![]() $\alpha $
-true to
$\alpha $
-true to
![]() $\tau $
. The terminology “true stage” comes from the application to computable constructions, as we discuss below. The idea is that in an x-computable construction,
$\tau $
. The terminology “true stage” comes from the application to computable constructions, as we discuss below. The idea is that in an x-computable construction,
![]() $x\! \upharpoonright \!{s}$
is the stage s information we have, and
$x\! \upharpoonright \!{s}$
is the stage s information we have, and
![]() $(x\! \upharpoonright \!{s})^{(\alpha )}$
is our stage s guess about
$(x\! \upharpoonright \!{s})^{(\alpha )}$
is our stage s guess about
![]() $x^{(\alpha )}$
; s is an
$x^{(\alpha )}$
; s is an
![]() $(x,\alpha )$
-true stage if
$(x,\alpha )$
-true stage if
![]() $x\! \upharpoonright \!{s}\prec _\alpha x$
.
$x\! \upharpoonright \!{s}\prec _\alpha x$
.
This definition of
![]() $\preceq _\alpha $
is not quite right. It needs to be modified in order to deal with limit ordinals. In this sketch we will ignore this modification; the definition
$\preceq _\alpha $
is not quite right. It needs to be modified in order to deal with limit ordinals. In this sketch we will ignore this modification; the definition
![]() $\sigma \preceq _\alpha \tau \,\,\Longleftrightarrow \,\, \sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
conveys the main idea. The nested condition TSP(5) results from the fact that since the Turing jump operator is defined by recursion on the ordinal, in order to compute
$\sigma \preceq _\alpha \tau \,\,\Longleftrightarrow \,\, \sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
conveys the main idea. The nested condition TSP(5) results from the fact that since the Turing jump operator is defined by recursion on the ordinal, in order to compute
![]() $\sigma ^{(\beta )}$
, we need to first, in some sense, compute
$\sigma ^{(\beta )}$
, we need to first, in some sense, compute
![]() $\sigma ^{(\alpha )}$
for all
$\sigma ^{(\alpha )}$
for all
![]() $\alpha <\beta $
. TSP(6) reflects the fact that
$\alpha <\beta $
. TSP(6) reflects the fact that
![]() $x^{(\lambda )}$
is Turing equivalent to the infinite join
$x^{(\lambda )}$
is Turing equivalent to the infinite join
![]() $\bigoplus _{\alpha <\lambda }x^{(\alpha )}$
.
$\bigoplus _{\alpha <\lambda }x^{(\alpha )}$
.
The main difference between the developments in [Reference Greenberg and Turetsky16, Reference Montalbán43] is that the former first defines the strings
![]() $\sigma ^{(\alpha )}$
and then modifies the resulting relations
$\sigma ^{(\alpha )}$
and then modifies the resulting relations
![]() $\preceq _\alpha $
, whereas the latter gives a simultaneous inductive definition of both
$\preceq _\alpha $
, whereas the latter gives a simultaneous inductive definition of both
![]() $\sigma ^{(\alpha )}$
and
$\sigma ^{(\alpha )}$
and
![]() $\preceq _\alpha $
.
$\preceq _\alpha $
.
2.1.1 A single step
Here we sketch out a single step, i.e., the construction of
![]() $\sigma ^{(\alpha +1)}$
from
$\sigma ^{(\alpha +1)}$
from
![]() $\sigma ^{(\alpha )}$
. The reader not interested in peeking under the hood may safely skip down to TSP(7).
$\sigma ^{(\alpha )}$
. The reader not interested in peeking under the hood may safely skip down to TSP(7).
For each x and
![]() $\alpha $
,
$\alpha $
,
![]() $x^{(\alpha +1)}$
is an element of Baire space which is Turing equivalent to
$x^{(\alpha +1)}$
is an element of Baire space which is Turing equivalent to
![]() $(x^{(\alpha )})'$
, the halting problem relative to
$(x^{(\alpha )})'$
, the halting problem relative to
![]() $x^{(\alpha )}$
. Fix a universal oracle Turing machine M which enumerates the jump: for all x and e,
$x^{(\alpha )}$
. Fix a universal oracle Turing machine M which enumerates the jump: for all x and e,
![]() $e\in x'$
if and only if
$e\in x'$
if and only if
![]() $M^x(e)\!\!\downarrow $
, i.e., the machine M with oracle x halts on input e. For a finite
$M^x(e)\!\!\downarrow $
, i.e., the machine M with oracle x halts on input e. For a finite
![]() $\sigma $
, we let
$\sigma $
, we let
![]() $\sigma '$
be the collection of e such that
$\sigma '$
be the collection of e such that
![]() $M^\sigma _{|\sigma |}(e)\!\!\downarrow $
, i.e., those e for which the machine M, with oracle
$M^\sigma _{|\sigma |}(e)\!\!\downarrow $
, i.e., those e for which the machine M, with oracle
![]() $\sigma $
, halts on input e in at most
$\sigma $
, halts on input e in at most
![]() $|\sigma |$
many steps.
$|\sigma |$
many steps.
For each finite sequence
![]() $\sigma \in \omega ^{<\omega }$
, the sequence
$\sigma \in \omega ^{<\omega }$
, the sequence
![]() $\sigma ^{(\alpha +1)}$
will encode a finite initial segment of
$\sigma ^{(\alpha +1)}$
will encode a finite initial segment of
![]() $(\sigma ^{(\alpha )})'$
: for some
$(\sigma ^{(\alpha )})'$
: for some
![]() $p_\alpha (\sigma )\in \mathbb N$
, for all
$p_\alpha (\sigma )\in \mathbb N$
, for all
![]() $e<p_\alpha (\sigma )$
,
$e<p_\alpha (\sigma )$
,
![]() $\sigma ^{(\alpha +1)}$
tells us whether
$\sigma ^{(\alpha +1)}$
tells us whether
![]() $e\in (\sigma ^{(\alpha )})'$
or not. The idea is the following: if
$e\in (\sigma ^{(\alpha )})'$
or not. The idea is the following: if
![]() $e\in (\sigma ^{(\alpha )})'$
then
$e\in (\sigma ^{(\alpha )})'$
then
![]() $\sigma $
can be confident that e is in the jump—for all infinite x, if
$\sigma $
can be confident that e is in the jump—for all infinite x, if
![]() $\sigma \prec _\alpha x$
then
$\sigma \prec _\alpha x$
then
![]() $e\in (x^{(\alpha )})'$
. For
$e\in (x^{(\alpha )})'$
. For
![]() $e<p_\alpha (\sigma )$
such that
$e<p_\alpha (\sigma )$
such that
![]() $e\notin (\sigma ^{(\alpha )})'$
,
$e\notin (\sigma ^{(\alpha )})'$
,
![]() $\sigma $
is sufficiently brave to declare that
$\sigma $
is sufficiently brave to declare that
![]() $e\notin (x^{(\alpha )})'$
for
$e\notin (x^{(\alpha )})'$
for
![]() $x\succ _\alpha \sigma $
; it may be correct about some such x’s, but not about others. For
$x\succ _\alpha \sigma $
; it may be correct about some such x’s, but not about others. For
![]() $e\geqslant p_\alpha (\sigma )$
,
$e\geqslant p_\alpha (\sigma )$
,
![]() $\sigma $
makes no commitment about
$\sigma $
makes no commitment about
![]() $(x^{(\alpha )})'(e)$
.
$(x^{(\alpha )})'(e)$
.
If
![]() $\sigma \prec _\alpha \tau $
, then as
$\sigma \prec _\alpha \tau $
, then as
![]() $\sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
, we have
$\sigma ^{(\alpha )}\preceq \tau ^{(\alpha )}$
, we have
![]() $(\sigma ^{(\alpha )})'\subseteq (\tau ^{(\alpha )})'$
: if the machine M with oracle
$(\sigma ^{(\alpha )})'\subseteq (\tau ^{(\alpha )})'$
: if the machine M with oracle
![]() $\sigma ^{(\alpha )}$
halts on e in at most
$\sigma ^{(\alpha )}$
halts on e in at most
![]() $|\sigma ^{(\alpha )}|$
many steps, then this also holds when the oracle is extended to
$|\sigma ^{(\alpha )}|$
many steps, then this also holds when the oracle is extended to
![]() $\tau ^{(\alpha )}$
(and more steps are allowed). We let
$\tau ^{(\alpha )}$
(and more steps are allowed). We let
![]() $\sigma \preceq _{\alpha +1} \tau $
if
$\sigma \preceq _{\alpha +1} \tau $
if
![]() $\sigma \prec _\alpha \tau $
and
$\sigma \prec _\alpha \tau $
and
![]() $\tau $
has no proof that
$\tau $
has no proof that
![]() $\sigma $
was wrong about
$\sigma $
was wrong about
![]() $(\sigma ^{(\alpha )})'\! \upharpoonright \!{p_\alpha (\sigma )}$
: if for all
$(\sigma ^{(\alpha )})'\! \upharpoonright \!{p_\alpha (\sigma )}$
: if for all
![]() $e<p_\alpha (\sigma )$
, if
$e<p_\alpha (\sigma )$
, if
![]() $e\notin (\sigma ^{(\alpha )})'$
then also
$e\notin (\sigma ^{(\alpha )})'$
then also
![]() $e\notin (\tau ^{(\alpha )})'$
.
$e\notin (\tau ^{(\alpha )})'$
.
Fixing
![]() $x\in \mathcal {N}$
, our goal is to ensure, for each
$x\in \mathcal {N}$
, our goal is to ensure, for each
![]() $\alpha $
, that:
$\alpha $
, that:
-
(*)
 $x^{(\alpha )} = \bigcup \left \{ \sigma ^{(\alpha )} \,:\, \sigma \prec _\alpha x \right \}$
.
$x^{(\alpha )} = \bigcup \left \{ \sigma ^{(\alpha )} \,:\, \sigma \prec _\alpha x \right \}$
.
That is, there are infinitely many
![]() $\alpha $
-true initial segments of x, and as they get longer, they give us more and more information about
$\alpha $
-true initial segments of x, and as they get longer, they give us more and more information about
![]() $x^{(\alpha )}$
. Suppose that (
$x^{(\alpha )}$
. Suppose that (
![]() $*$
) is known for some
$*$
) is known for some
![]() $\alpha $
. To ensure that (
$\alpha $
. To ensure that (
![]() $*$
) also holds for
$*$
) also holds for
![]() $\alpha +1$
, we need to define
$\alpha +1$
, we need to define
![]() $p_\alpha (\sigma )$
wisely. The main idea is that of the “non-deficiency stages” of Dekker, in his construction of a hypersimple set in every c.e. degree [Reference Dekker11]. We fix an enumeration of the jump sets
$p_\alpha (\sigma )$
wisely. The main idea is that of the “non-deficiency stages” of Dekker, in his construction of a hypersimple set in every c.e. degree [Reference Dekker11]. We fix an enumeration of the jump sets
![]() $\sigma '$
so that if
$\sigma '$
so that if
![]() $\sigma \preceq \tau $
then the enumeration of
$\sigma \preceq \tau $
then the enumeration of
![]() $\tau '$
extends that of
$\tau '$
extends that of
![]() $\sigma '$
; we let
$\sigma '$
; we let
![]() $p_\alpha (\sigma )$
be the last number enumerated into
$p_\alpha (\sigma )$
be the last number enumerated into
![]() $(\sigma ^{(\alpha )})'$
. So
$(\sigma ^{(\alpha )})'$
. So
![]() $\sigma $
observes that the number
$\sigma $
observes that the number
![]() $p = p_\alpha (\sigma )$
has just entered
$p = p_\alpha (\sigma )$
has just entered
![]() $(\sigma ^{(\alpha )})'$
; it thinks that no smaller numbers will enter the jump later, but is not willing to give an opinion about larger ones. To verify (
$(\sigma ^{(\alpha )})'$
; it thinks that no smaller numbers will enter the jump later, but is not willing to give an opinion about larger ones. To verify (
![]() $*$
), for any
$*$
), for any
![]() $\sigma \prec _\alpha x$
, let k be the least element of
$\sigma \prec _\alpha x$
, let k be the least element of
![]() $(x^{(\alpha )})'\setminus (\sigma ^{(\alpha )})'$
. By (
$(x^{(\alpha )})'\setminus (\sigma ^{(\alpha )})'$
. By (
![]() $*$
) for
$*$
) for
![]() $\alpha $
, for sufficiently long
$\alpha $
, for sufficiently long
![]() $\tau \prec _\alpha x$
we have
$\tau \prec _\alpha x$
we have
![]() $k\in (\tau ^{(\alpha )})'$
; the least such
$k\in (\tau ^{(\alpha )})'$
; the least such
![]() $\tau $
will have
$\tau $
will have
![]() $k = p_\alpha (\tau )$
and so
$k = p_\alpha (\tau )$
and so
![]() $\tau \prec _{\alpha +1}x$
.
$\tau \prec _{\alpha +1}x$
.
While the actual details are a little different, we can now state another important property of the true stages machinery:
-
TSP(7): There are functions
 $p_\alpha \colon \omega ^{<\omega }\to \mathbb N$
such that for all
$p_\alpha \colon \omega ^{<\omega }\to \mathbb N$
such that for all
 $\sigma ,\tau \in \omega ^{<\omega }$
,
$\sigma ,\tau \in \omega ^{<\omega }$
,
 $\sigma \prec _{\alpha +1}\tau $
if and only if
$\sigma \prec _{\alpha +1}\tau $
if and only if
 $\sigma \prec _\alpha \tau $
and for all finite
$\sigma \prec _\alpha \tau $
and for all finite
 $\rho $
satisfying
$\rho $
satisfying
 $\sigma \prec _\alpha \rho \preceq _{\alpha }\tau $
we have
$\sigma \prec _\alpha \rho \preceq _{\alpha }\tau $
we have
 $p_\alpha (\rho )\geqslant p_\alpha (\sigma )$
.
$p_\alpha (\rho )\geqslant p_\alpha (\sigma )$
.
(
![]() $*$
) can also explain TSP(4); we give a sketch. We remark though that when developing the true stage relations in [Reference Day, Greenberg, Harrison-Trainor and Turetsky8], the property TSP(4) is derived directly from the definitions, without referring to iterated jumps, and in fact, (
$*$
) can also explain TSP(4); we give a sketch. We remark though that when developing the true stage relations in [Reference Day, Greenberg, Harrison-Trainor and Turetsky8], the property TSP(4) is derived directly from the definitions, without referring to iterated jumps, and in fact, (
![]() $*$
) can then be derived from TSP(4).
$*$
) can then be derived from TSP(4).
Sketch of derivation of TSP(4):
In one direction, let A be
![]() $\Sigma ^0_{1+\alpha }$
; let V be given by Proposition 2.3. There is a c.e. set of strings
$\Sigma ^0_{1+\alpha }$
; let V be given by Proposition 2.3. There is a c.e. set of strings
![]() $V_0$
, closed under taking extensions, that generates V as an open set. By (
$V_0$
, closed under taking extensions, that generates V as an open set. By (
![]() $*$
),
$*$
),
![]() ${U = \{ \sigma \in \omega ^{<\omega } \,:\, \sigma ^{(\alpha )}\in V_0 \}}$
is as required for TSP(4). In the other direction, for each x,
${U = \{ \sigma \in \omega ^{<\omega } \,:\, \sigma ^{(\alpha )}\in V_0 \}}$
is as required for TSP(4). In the other direction, for each x,
![]() $\left \{ \sigma \,:\, \sigma \prec _\alpha x \right \}$
is
$\left \{ \sigma \,:\, \sigma \prec _\alpha x \right \}$
is
![]() $x^{(\alpha )}$
-computable, uniformly in x. That is, there is some
$x^{(\alpha )}$
-computable, uniformly in x. That is, there is some
![]() $\Delta ^0_1$
set
$\Delta ^0_1$
set
![]() $W\subset \omega ^{<\omega }\times \mathcal {N}$
such that
$W\subset \omega ^{<\omega }\times \mathcal {N}$
such that
![]() ${\sigma \prec _\alpha x \,\,\Longleftrightarrow \,\, (\sigma ,x^{(\alpha )})\in W}$
. Proposition 2.3 then implies that
${\sigma \prec _\alpha x \,\,\Longleftrightarrow \,\, (\sigma ,x^{(\alpha )})\in W}$
. Proposition 2.3 then implies that
![]() $[\sigma ]^\prec _\alpha $
is
$[\sigma ]^\prec _\alpha $
is
![]() $\Delta ^0_{1+\alpha }$
, uniformly in
$\Delta ^0_{1+\alpha }$
, uniformly in
![]() $\sigma $
. We mention that we have implicitly used TSP(8), stated below. We also remark that TSP(4) is uniform: we can effectively pass from
$\sigma $
. We mention that we have implicitly used TSP(8), stated below. We also remark that TSP(4) is uniform: we can effectively pass from
![]() $\Sigma ^0_{1+\alpha }$
indices of A to c.e. indices of U.
$\Sigma ^0_{1+\alpha }$
indices of A to c.e. indices of U.
What we have not discussed so far is how to ensure that (
![]() $*$
) holds for limit ordinals
$*$
) holds for limit ordinals
![]() $\alpha $
. This is, in fact, the most difficult aspect of the construction of the true stages machinery. In [Reference Greenberg and Turetsky16], this is solved by the particular encoding of the iterated jumps into
$\alpha $
. This is, in fact, the most difficult aspect of the construction of the true stages machinery. In [Reference Greenberg and Turetsky16], this is solved by the particular encoding of the iterated jumps into
![]() $\sigma ^{(\alpha )}$
; a kind of diagonal intersection argument is used. We will further discuss limit levels in the next section.
$\sigma ^{(\alpha )}$
; a kind of diagonal intersection argument is used. We will further discuss limit levels in the next section.
For a final remark, we observe that like the set
![]() $x^{(\alpha )}$
(and unlike its Turing degree), the partial orderings
$x^{(\alpha )}$
(and unlike its Turing degree), the partial orderings
![]() $\preceq _\alpha $
actually depend on the choice of a computable well-ordering of
$\preceq _\alpha $
actually depend on the choice of a computable well-ordering of
![]() $\mathbb N$
of order-type
$\mathbb N$
of order-type
![]() $\alpha $
. For this reason, we cannot define
$\alpha $
. For this reason, we cannot define
![]() $\preceq _\alpha $
in a way that will satisfy TSP(5), TSP(6), and other nice properties for all computable ordinals at once. In [Reference Greenberg and Turetsky16], this obstacle is overcome by an overspill argument, in which the true stages machinery is applied to a pseudo-ordinal
$\preceq _\alpha $
in a way that will satisfy TSP(5), TSP(6), and other nice properties for all computable ordinals at once. In [Reference Greenberg and Turetsky16], this obstacle is overcome by an overspill argument, in which the true stages machinery is applied to a pseudo-ordinal
![]() $\delta ^*>\omega _1^{\text {ck}}$
. The price to pay then is having to ensure that these pseudo-ordinals do not interfere with the intended construction.
$\delta ^*>\omega _1^{\text {ck}}$
. The price to pay then is having to ensure that these pseudo-ordinals do not interfere with the intended construction.
2.1.2 Iterated priority arguments
In order to apply true stages to iterated priority arguments, which are computable constructions, we require:
-
TSP(8): The restriction of the relation
 $\preceq _\alpha $
to
$\preceq _\alpha $
to
 $\omega ^{<\omega }$
(i.e., to finite sequences) is computable. So is the map
$\omega ^{<\omega }$
(i.e., to finite sequences) is computable. So is the map
 $\sigma \mapsto \sigma ^{(\alpha )}$
for finite
$\sigma \mapsto \sigma ^{(\alpha )}$
for finite
 $\sigma $
, and the function
$\sigma $
, and the function
 $p_\alpha $
of TSP(7).
$p_\alpha $
of TSP(7).
Note that in contrast, for each infinite x, the relation
![]() $\sigma \prec _\alpha x$
is
$\sigma \prec _\alpha x$
is
![]() $\Delta ^0_{1+\alpha }(x)$
, and cannot be any simpler.
$\Delta ^0_{1+\alpha }(x)$
, and cannot be any simpler.
TSP(8) allows us to use the guesses
![]() $\sigma ^{(\alpha )}$
during a computable construction, and also observe, at every stage
$\sigma ^{(\alpha )}$
during a computable construction, and also observe, at every stage
![]() $t<\omega $
, the opinion at stage t about the
$t<\omega $
, the opinion at stage t about the
![]() $\alpha $
-truth of previous stages.
$\alpha $
-truth of previous stages.
Let us sketch how this is used in computable structure theory. As was our description of the development of the true stages machinery, this will be a very rough sketch, and it will not be essential for the remainder of the paper. Here we construct a single computable structure, so we apply the true stages machinery (as it was originally devised) to
![]() $x = 0^\infty $
. For
$x = 0^\infty $
. For
![]() $s,t\leqslant \omega $
, we write
$s,t\leqslant \omega $
, we write
![]() $s\leqslant _\alpha t$
to denote
$s\leqslant _\alpha t$
to denote
![]() $0^s\preceq _\alpha 0^t$
, and say that s appears to be
$0^s\preceq _\alpha 0^t$
, and say that s appears to be
![]() $\alpha $
-true at t; when
$\alpha $
-true at t; when
![]() $t = \omega $
, we say that s is
$t = \omega $
, we say that s is
![]() $\alpha $
-true.
$\alpha $
-true.
Let
![]() $\delta $
be a computable ordinal. Suppose that we wish to construct a computable structure
$\delta $
be a computable ordinal. Suppose that we wish to construct a computable structure
![]() $\mathcal {M}$
and at the same time encode some
$\mathcal {M}$
and at the same time encode some
![]() $\emptyset ^{(\delta )}$
-computable information into the computable
$\emptyset ^{(\delta )}$
-computable information into the computable
![]() $\Pi ^0_\delta $
-diagram of
$\Pi ^0_\delta $
-diagram of
![]() $\mathcal {M}$
(the relations on
$\mathcal {M}$
(the relations on
![]() $\mathcal {M}$
defined by the computable
$\mathcal {M}$
defined by the computable
![]() $\forall _\delta $
-fragment of
$\forall _\delta $
-fragment of
![]() $\mathcal {L}_{\omega _1,\omega }$
in the language of
$\mathcal {L}_{\omega _1,\omega }$
in the language of
![]() $\mathcal {M}$
). For example, in the Ash–Watnick theorem mentioned above, we are given a
$\mathcal {M}$
). For example, in the Ash–Watnick theorem mentioned above, we are given a
![]() $\emptyset ^{(2\delta )}$
-computable linear ordering
$\emptyset ^{(2\delta )}$
-computable linear ordering
![]() $\mathcal {L}$
, and we need to construct a linear ordering
$\mathcal {L}$
, and we need to construct a linear ordering
![]() $\mathcal {M}$
of order-type
$\mathcal {M}$
of order-type
![]() $\mathbb Z^\delta \cdot \mathcal {L}$
; the
$\mathbb Z^\delta \cdot \mathcal {L}$
; the
![]() $\Pi ^0_{2\delta }$
relation that interests us is whether two elements of
$\Pi ^0_{2\delta }$
relation that interests us is whether two elements of
![]() $\mathcal {M}$
are in the same copy of
$\mathcal {M}$
are in the same copy of
![]() $\mathbb Z^\delta $
, i.e., whether they are identified after applying the Hausdorff derivative (identify points which are finitely far apart)
$\mathbb Z^\delta $
, i.e., whether they are identified after applying the Hausdorff derivative (identify points which are finitely far apart)
![]() $\delta $
many times.Footnote
1
$\delta $
many times.Footnote
1
During the construction, at each stage
![]() $s<\omega $
, we construct not only a finite substructure
$s<\omega $
, we construct not only a finite substructure
![]() $\mathcal {M}_s$
of the intended computable structure
$\mathcal {M}_s$
of the intended computable structure
![]() $\mathcal {M} = \mathcal {M}_\omega $
, but also an approximation
$\mathcal {M} = \mathcal {M}_\omega $
, but also an approximation
![]() $\mathcal {D}^\delta _s$
of the
$\mathcal {D}^\delta _s$
of the
![]() $\Pi ^0_\delta $
diagram of
$\Pi ^0_\delta $
diagram of
![]() $\mathcal {M}$
. We use our guess
$\mathcal {M}$
. We use our guess
![]() $\emptyset _s^{(\delta )} = (0^s)^{(\delta )}$
of
$\emptyset _s^{(\delta )} = (0^s)^{(\delta )}$
of
![]() $\emptyset ^{(\delta )}$
to determine which statements to include in
$\emptyset ^{(\delta )}$
to determine which statements to include in
![]() $\mathcal {D}_s^\delta $
.
$\mathcal {D}_s^\delta $
.
We require that
![]() $\mathcal {M}_s\subseteq \mathcal {M}_t$
when
$\mathcal {M}_s\subseteq \mathcal {M}_t$
when
![]() $s\leqslant t$
. Since the construction is computable, the sequence
$s\leqslant t$
. Since the construction is computable, the sequence
![]() $\langle {\mathcal {M}_s}\rangle $
is computable, and so
$\langle {\mathcal {M}_s}\rangle $
is computable, and so
![]() $\mathcal {M} = \mathcal {M}_\omega = \bigcup _s \mathcal {M}_s$
is a computable structure, as required. Further, and this is the key point, we ensure that for
$\mathcal {M} = \mathcal {M}_\omega = \bigcup _s \mathcal {M}_s$
is a computable structure, as required. Further, and this is the key point, we ensure that for
![]() $s \leqslant _\delta t$
,
$s \leqslant _\delta t$
,
![]() $\mathcal {D}^\delta _s \subseteq \mathcal {D}^\delta _t$
. What is useful to us at the end is that when
$\mathcal {D}^\delta _s \subseteq \mathcal {D}^\delta _t$
. What is useful to us at the end is that when
![]() $s<_\delta \omega $
(s is a
$s<_\delta \omega $
(s is a
![]() $\delta $
-true stage),
$\delta $
-true stage),
![]() $\mathcal {D}^\delta _s \subset \mathcal {D}^\delta _\omega $
, the latter being the true
$\mathcal {D}^\delta _s \subset \mathcal {D}^\delta _\omega $
, the latter being the true
![]() $\Pi ^0_\delta $
-diagram of
$\Pi ^0_\delta $
-diagram of
![]() $\mathcal {M} = \mathcal {M}_\omega $
. For such s, the choices we make for
$\mathcal {M} = \mathcal {M}_\omega $
. For such s, the choices we make for
![]() $\mathcal {D}^\delta _s$
are correct, since our guess
$\mathcal {D}^\delta _s$
are correct, since our guess
![]() $\emptyset ^{(\delta )}_s$
about
$\emptyset ^{(\delta )}_s$
about
![]() $\emptyset ^{(\delta )}$
is correct. Further, since
$\emptyset ^{(\delta )}$
is correct. Further, since
![]() $\emptyset ^{(\delta )} = \bigcup \{\emptyset ^{(\delta )}_s\,:\, s<_\delta \omega \}$
(every
$\emptyset ^{(\delta )} = \bigcup \{\emptyset ^{(\delta )}_s\,:\, s<_\delta \omega \}$
(every
![]() $\delta $
-correct piece of information is eventually revealed at
$\delta $
-correct piece of information is eventually revealed at
![]() $\delta $
-true stages), we get
$\delta $
-true stages), we get
![]() $\mathcal {D}^\delta _\omega = \bigcup \{ \mathcal {D}^\delta _s \,:\, s<_\delta \omega \}$
. That is, every
$\mathcal {D}^\delta _\omega = \bigcup \{ \mathcal {D}^\delta _s \,:\, s<_\delta \omega \}$
. That is, every
![]() $\Pi ^0_\delta $
fact is eventually correctly decided on the
$\Pi ^0_\delta $
fact is eventually correctly decided on the
![]() $\delta $
-true stages. Note that the entire construction is computable: the map
$\delta $
-true stages. Note that the entire construction is computable: the map
![]() $s\mapsto \emptyset ^{(\delta )}_s$
, and so the map
$s\mapsto \emptyset ^{(\delta )}_s$
, and so the map
![]() $s\mapsto \mathcal {D}^\delta _s$
, are computable. The reason that
$s\mapsto \mathcal {D}^\delta _s$
, are computable. The reason that
![]() $\mathcal {D}^\delta _\omega $
is not computable is that
$\mathcal {D}^\delta _\omega $
is not computable is that
![]() $\{s\,:\, s<_\delta \omega \}$
is not computable; the complexity is encoded in the set of
$\{s\,:\, s<_\delta \omega \}$
is not computable; the complexity is encoded in the set of
![]() $\delta $
-true stages. Since that set is not computable, we need to ensure that
$\delta $
-true stages. Since that set is not computable, we need to ensure that
![]() $\mathcal {D}^\delta _s\subseteq \mathcal {D}^\delta _t$
when
$\mathcal {D}^\delta _s\subseteq \mathcal {D}^\delta _t$
when
![]() $s\leqslant _\delta t$
, even if s is not
$s\leqslant _\delta t$
, even if s is not
![]() $\delta $
-true.
$\delta $
-true.
One might wonder how we ensure that
![]() $\bigcup \left \{ \mathcal {D}^\delta _s \,:\, s<_\delta \omega \right \}$
is in fact the
$\bigcup \left \{ \mathcal {D}^\delta _s \,:\, s<_\delta \omega \right \}$
is in fact the
![]() $\Pi ^0_\delta $
-diagram of
$\Pi ^0_\delta $
-diagram of
![]() $\mathcal {M}$
. For example, at
$\mathcal {M}$
. For example, at
![]() $\delta $
-true stages of the Ash–Watnick construction, we may declare that two elements a and b of
$\delta $
-true stages of the Ash–Watnick construction, we may declare that two elements a and b of
![]() $\mathcal {M}$
are in the same copy of
$\mathcal {M}$
are in the same copy of
![]() $\mathbb Z^\delta $
(or not). How do we ensure that this declaration is in fact correct in the structure
$\mathbb Z^\delta $
(or not). How do we ensure that this declaration is in fact correct in the structure
![]() $\mathcal {M}$
? Note that at each stage s,
$\mathcal {M}$
? Note that at each stage s,
![]() $\mathcal {M}_s$
is a finite linear ordering, so the declaration at that stage is just that: a declaration of intention, a promise about how the structure will be built from now on. For this purpose, we in fact not only make promises about the
$\mathcal {M}_s$
is a finite linear ordering, so the declaration at that stage is just that: a declaration of intention, a promise about how the structure will be built from now on. For this purpose, we in fact not only make promises about the
![]() $\Pi ^0_\delta $
-diagram, but for all
$\Pi ^0_\delta $
-diagram, but for all
![]() $\alpha \leqslant \delta $
, we give an approximation
$\alpha \leqslant \delta $
, we give an approximation
![]() $\mathcal {D}^\alpha _s$
of the
$\mathcal {D}^\alpha _s$
of the
![]() $\Pi ^0_\alpha $
-diagram of
$\Pi ^0_\alpha $
-diagram of
![]() $\mathcal {M}$
. In the Ash–Watnick example, at level
$\mathcal {M}$
. In the Ash–Watnick example, at level
![]() $2\alpha $
we declare which points are identified after
$2\alpha $
we declare which points are identified after
![]() $\alpha $
many iterations of the Hausdorff derivative; at level
$\alpha $
many iterations of the Hausdorff derivative; at level
![]() $2\alpha +1$
we decide the successor relation on the
$2\alpha +1$
we decide the successor relation on the
![]() $\alpha {}^{\text {th}}$
-derivative ordering. Each
$\alpha {}^{\text {th}}$
-derivative ordering. Each
![]() $\mathcal {D}^\alpha _s$
is decided based on the approximation
$\mathcal {D}^\alpha _s$
is decided based on the approximation
![]() $\emptyset ^{(\alpha )}_s$
of
$\emptyset ^{(\alpha )}_s$
of
![]() $\emptyset ^{(\alpha )}$
. The
$\emptyset ^{(\alpha )}$
. The
![]() $\Pi ^0_{\alpha +1}$
-diagram of a structure can be recovered from the
$\Pi ^0_{\alpha +1}$
-diagram of a structure can be recovered from the
![]() $\Pi ^0_\alpha $
-diagram; at every stage s, we build
$\Pi ^0_\alpha $
-diagram; at every stage s, we build
![]() $\mathcal {D}^\alpha _s$
so that
$\mathcal {D}^\alpha _s$
so that
![]() $\mathcal {D}^{\alpha +1}_s$
is consistent with the diagram recovered in this fashion from
$\mathcal {D}^{\alpha +1}_s$
is consistent with the diagram recovered in this fashion from
![]() $\mathcal {D}^\alpha _s$
. We then let
$\mathcal {D}^\alpha _s$
. We then let
![]() $\mathcal {D}^\alpha _\omega = \bigcup \left \{ \mathcal {D}^\alpha _s \,:\, s<_\alpha \omega \right \}$
, and inductively show that
$\mathcal {D}^\alpha _\omega = \bigcup \left \{ \mathcal {D}^\alpha _s \,:\, s<_\alpha \omega \right \}$
, and inductively show that
![]() $\mathcal {D}^\alpha _\omega $
is indeed the correct diagram at its level. (We are eliding how limit levels are dealt with.)
$\mathcal {D}^\alpha _\omega $
is indeed the correct diagram at its level. (We are eliding how limit levels are dealt with.)
The overall resulting requirement for the construction is: for all
![]() $\alpha \leqslant \delta $
, if
$\alpha \leqslant \delta $
, if
![]() $s\leqslant _\alpha t$
then
$s\leqslant _\alpha t$
then
![]() $\mathcal {D}^\alpha _s \subseteq \mathcal {D}^\alpha _t$
. (The requirement
$\mathcal {D}^\alpha _s \subseteq \mathcal {D}^\alpha _t$
. (The requirement
![]() $\mathcal {M}_s\subseteq \mathcal {M}_t$
is incorporated into this, as
$\mathcal {M}_s\subseteq \mathcal {M}_t$
is incorporated into this, as
![]() $\mathcal {D}^0_s$
is essentially the atomic diagram of
$\mathcal {D}^0_s$
is essentially the atomic diagram of
![]() $\mathcal {M}_s$
; and
$\mathcal {M}_s$
; and
![]() $s\leqslant _0 t$
iff
$s\leqslant _0 t$
iff
![]() $s\leqslant t$
.) As
$s\leqslant t$
.) As
![]() $\leqslant _{\alpha +1}$
branches more than
$\leqslant _{\alpha +1}$
branches more than
![]() $\leqslant _\alpha $
, we will sometimes have the following scenario:
$\leqslant _\alpha $
, we will sometimes have the following scenario:
![]() $r <_\alpha s <_\alpha t$
with
$r <_\alpha s <_\alpha t$
with
![]() $r <_{\alpha +1} t$
and
$r <_{\alpha +1} t$
and
![]() $s \not <_{\alpha +1} t$
. Then we must have
$s \not <_{\alpha +1} t$
. Then we must have
![]() $\mathcal {D}^\alpha _r \subseteq \mathcal {D}^\alpha _s \subseteq \mathcal {D}^\alpha _t$
; however,
$\mathcal {D}^\alpha _r \subseteq \mathcal {D}^\alpha _s \subseteq \mathcal {D}^\alpha _t$
; however,
![]() $\mathcal {D}^\alpha _s$
was built to support
$\mathcal {D}^\alpha _s$
was built to support
![]() $\mathcal {D}^{\alpha +1}_s$
, and it may be that
$\mathcal {D}^{\alpha +1}_s$
, and it may be that
![]() $\mathcal {D}^{\alpha +1}_s \not \subseteq \mathcal {D}^{\alpha +1}_t$
. So our construction must be such that our work for level
$\mathcal {D}^{\alpha +1}_s \not \subseteq \mathcal {D}^{\alpha +1}_t$
. So our construction must be such that our work for level
![]() $\alpha $
at stage s can be folded into our work at stage t. Arguing this is generally the main labor for a true stages priority argument. One advantage we have is the following property, denoted
$\alpha $
at stage s can be folded into our work at stage t. Arguing this is generally the main labor for a true stages priority argument. One advantage we have is the following property, denoted
![]() $(\clubsuit )$
by Montalbán:
$(\clubsuit )$
by Montalbán:
-
(♣) If
 $\sigma _0 \preceq _{\alpha } \sigma _1 \preceq _\alpha \sigma _2$
and
$\sigma _0 \preceq _{\alpha } \sigma _1 \preceq _\alpha \sigma _2$
and
 $\sigma _0 \preceq _{\alpha +1} \sigma _2$
, then
$\sigma _0 \preceq _{\alpha +1} \sigma _2$
, then
 $\sigma _0 \preceq _{\alpha +1} \sigma _1$
.
$\sigma _0 \preceq _{\alpha +1} \sigma _1$
.
In our scenario, it follows that
![]() $r <_{\alpha +1} s$
, and so
$r <_{\alpha +1} s$
, and so
![]() $\mathcal {D}_r^{\alpha +1} \subseteq \mathcal {D}_s^{\alpha +1}$
, so the work for
$\mathcal {D}_r^{\alpha +1} \subseteq \mathcal {D}_s^{\alpha +1}$
, so the work for
![]() $\alpha $
at stage s at least was not violating
$\alpha $
at stage s at least was not violating
![]() $\mathcal {D}_r^{\alpha +1}$
. The property (♣) follows immediately from TSP(7). Informally, if
$\mathcal {D}_r^{\alpha +1}$
. The property (♣) follows immediately from TSP(7). Informally, if
![]() $\sigma _0^{(\alpha )}\preceq \sigma _1^{(\alpha )} \preceq \sigma _2^{(\alpha )}$
, and
$\sigma _0^{(\alpha )}\preceq \sigma _1^{(\alpha )} \preceq \sigma _2^{(\alpha )}$
, and
![]() $\sigma _2$
has no evidence that
$\sigma _2$
has no evidence that
![]() $\sigma _0$
was wrong about
$\sigma _0$
was wrong about
![]() $(\sigma _0^{(\alpha )})^{\prime }$
, then
$(\sigma _0^{(\alpha )})^{\prime }$
, then
![]() $\sigma _1$
cannot have any such evidence either.
$\sigma _1$
cannot have any such evidence either.
Remark 2.5. As mentioned above, in [Reference Debs and Raymond10], Debs and Saint Raymond developed a representation machinery for Borel sets that shares features with the true stages method. In particular, they use (♣) as a fundamental concept, from which they derive other properties of their iterated tree representations.
3 Analysis of the ambiguous Borel classes
In this section we show how the true stages machinery allows us to give intuitive proofs of two theorems analysing the structure of the classes
![]() $\boldsymbol {\Delta }^0_\xi $
, in terms of how they are built from lower-level classes. For successor
$\boldsymbol {\Delta }^0_\xi $
, in terms of how they are built from lower-level classes. For successor
![]() $\xi $
, the Hausdorff–Kuratowski theorem gives an answer in terms of the Hausdorff difference hierarchy. For limit
$\xi $
, the Hausdorff–Kuratowski theorem gives an answer in terms of the Hausdorff difference hierarchy. For limit
![]() $\xi $
, Wadge gave an answer involving iterated partitioned unions.
$\xi $
, Wadge gave an answer involving iterated partitioned unions.
3.1 The Hausdorff–Kuratowski theorem
The Hausdorff difference hierarchy (sometimes also named after Lavrentiev) is a transfinite extension of a hierarchy of finite Boolean operations.
Definition 3.1. Let
![]() $\boldsymbol {\Gamma }$
be a boldface pointclass and let
$\boldsymbol {\Gamma }$
be a boldface pointclass and let
![]() $\eta \geqslant 1$
be a countable ordinal. We let
$\eta \geqslant 1$
be a countable ordinal. We let
![]() $D_\eta (\boldsymbol {\Gamma })$
be the class of all sets of the form
$D_\eta (\boldsymbol {\Gamma })$
be the class of all sets of the form
 $$\begin{align*}A = \bigcup \Big\{ (A_i \setminus \bigcup_{j < i} A_j) \, : \, i < \eta \,\,\,\&\,\,\, \text{parity}(i) \neq \text{parity}(\eta)\Big\}, \end{align*}$$
$$\begin{align*}A = \bigcup \Big\{ (A_i \setminus \bigcup_{j < i} A_j) \, : \, i < \eta \,\,\,\&\,\,\, \text{parity}(i) \neq \text{parity}(\eta)\Big\}, \end{align*}$$
where
![]() ${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
is an increasing sequence of sets from
${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
is an increasing sequence of sets from
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
Thus,
![]() $D_1(\boldsymbol {\Gamma }) = \boldsymbol {\Gamma }$
,
$D_1(\boldsymbol {\Gamma }) = \boldsymbol {\Gamma }$
,
![]() $D_{\eta +1}(\boldsymbol {\Gamma })$
is the collection of sets of the form
$D_{\eta +1}(\boldsymbol {\Gamma })$
is the collection of sets of the form
![]() $A\setminus B$
where
$A\setminus B$
where
![]() $A\in \boldsymbol {\Gamma }$
and
$A\in \boldsymbol {\Gamma }$
and
![]() $B\in D_\eta (\boldsymbol {\Gamma })$
, and for limit
$B\in D_\eta (\boldsymbol {\Gamma })$
, and for limit
![]() $\eta $
,
$\eta $
,
![]() $D_\eta (\boldsymbol {\Gamma })$
is the collection of sets of the form
$D_\eta (\boldsymbol {\Gamma })$
is the collection of sets of the form
![]() $\bigcup _{i<\eta } (A_{2i+1}\setminus A_{2i})$
where
$\bigcup _{i<\eta } (A_{2i+1}\setminus A_{2i})$
where
![]() ${\left \langle {A_i}\right \rangle }_{\alpha <\eta }$
is as in the definition.
${\left \langle {A_i}\right \rangle }_{\alpha <\eta }$
is as in the definition.
We similarly define
![]() $D_\eta (\Gamma )$
for lightface pointclasses; here we require that the sequence
$D_\eta (\Gamma )$
for lightface pointclasses; here we require that the sequence
![]() ${\left \langle {A_i}\right \rangle }$
be uniformly in
${\left \langle {A_i}\right \rangle }$
be uniformly in
![]() $\Gamma $
. As with the relations
$\Gamma $
. As with the relations
![]() $\prec _\alpha $
, the class will actually depend on the choice of a computable copy of
$\prec _\alpha $
, the class will actually depend on the choice of a computable copy of
![]() $\eta $
. The computability-theoretic analogue of the Hausdorff difference hierarchy is the Ershov hierarchy [Reference Ershov13], which has the same definition, where
$\eta $
. The computability-theoretic analogue of the Hausdorff difference hierarchy is the Ershov hierarchy [Reference Ershov13], which has the same definition, where
![]() $\Gamma $
is the class of c.e. subsets of
$\Gamma $
is the class of c.e. subsets of
![]() $\mathbb N$
. Ershov used the notation
$\mathbb N$
. Ershov used the notation
![]() $\Sigma ^{-1}_{\eta }$
for
$\Sigma ^{-1}_{\eta }$
for
![]() $D_\eta (\Sigma ^0_1(\mathbb N))$
.
$D_\eta (\Sigma ^0_1(\mathbb N))$
.
Hausdorff [Reference Hausdorff20, Chapter 8, Section 4] showed that
![]() $\boldsymbol {\Delta }^0_2 = \bigcup _{\eta <\omega _1} D_\eta (\boldsymbol {\Sigma }^0_1)$
; Kuratowski [Reference Kuratowski31, Chapter 37, Section 3] then used Proposition 2.2 to prove:
$\boldsymbol {\Delta }^0_2 = \bigcup _{\eta <\omega _1} D_\eta (\boldsymbol {\Sigma }^0_1)$
; Kuratowski [Reference Kuratowski31, Chapter 37, Section 3] then used Proposition 2.2 to prove:
Theorem 3.2 (Hausdorff–Kuratowski).
For all
![]() $1\leqslant \xi <\omega _1$
,
$1\leqslant \xi <\omega _1$
,
 $$\begin{align*}\boldsymbol{\Delta}^0_{\xi+1} = \bigcup_{\eta<\omega_1}D_\eta(\boldsymbol{\Sigma}^0_\xi). \end{align*}$$
$$\begin{align*}\boldsymbol{\Delta}^0_{\xi+1} = \bigcup_{\eta<\omega_1}D_\eta(\boldsymbol{\Sigma}^0_\xi). \end{align*}$$
See also [Reference Kechris22, Theorem 22.27]. The following effective version of the Hausdorff–Kuratowski theorem implies Theorem 3.2 by relativising to an oracle.
Theorem 3.3. For all computable
![]() $\xi \geqslant 1$
,
$\xi \geqslant 1$
,
 $$\begin{align*}\Delta^0_{\xi+1} = \bigcup_{\eta<\omega_1^{\text{ck}}}D_\eta(\Sigma^0_\xi). \end{align*}$$
$$\begin{align*}\Delta^0_{\xi+1} = \bigcup_{\eta<\omega_1^{\text{ck}}}D_\eta(\Sigma^0_\xi). \end{align*}$$
Remark 3.4. The effective version of Hausdorff’s theorem (Theorem 3.3 for
![]() $\xi = 1$
) was proved by Ershov for subsets of
$\xi = 1$
) was proved by Ershov for subsets of
![]() $\mathbb N$
and by Selivanov [Reference Selivanov50] for subsets of
$\mathbb N$
and by Selivanov [Reference Selivanov50] for subsets of
![]() $\mathcal {N}$
; see also [Reference Pauly47]. We remark again, however, that the lightface class
$\mathcal {N}$
; see also [Reference Pauly47]. We remark again, however, that the lightface class
![]() $D_\eta (\Gamma )$
heavily depends on the particular choice of computable copy of
$D_\eta (\Gamma )$
heavily depends on the particular choice of computable copy of
![]() $\eta $
. The theorem says that for every
$\eta $
. The theorem says that for every
![]() $\Delta ^0_{\xi +1}$
set A there is some computable well-ordering R such that
$\Delta ^0_{\xi +1}$
set A there is some computable well-ordering R such that
![]() $A\in D_R(\Sigma ^0_\xi )$
.
$A\in D_R(\Sigma ^0_\xi )$
.
For subsets of
![]() $\mathbb N$
, the situation is particularly dire; Ershov showed that every
$\mathbb N$
, the situation is particularly dire; Ershov showed that every
![]() $\Delta ^0_2$
subset of
$\Delta ^0_2$
subset of
![]() $\mathbb N$
is in
$\mathbb N$
is in
![]() $D_R(\Sigma ^0_1)$
for some computable copy R of
$D_R(\Sigma ^0_1)$
for some computable copy R of
![]() $\omega $
. The complexity of a set
$\omega $
. The complexity of a set
![]() $A\in \Delta ^0_2$
is coded into this copy of
$A\in \Delta ^0_2$
is coded into this copy of
![]() $\omega $
, rather than the sequence of sets
$\omega $
, rather than the sequence of sets
![]() ${\left \langle {A_i}\right \rangle }_{i<\omega }$
; the copy of
${\left \langle {A_i}\right \rangle }_{i<\omega }$
; the copy of
![]() $\omega $
may be a “bad copy,” in which the successor relation is not computable.
$\omega $
may be a “bad copy,” in which the successor relation is not computable.
For subsets of Baire space, topological considerations preclude such an anomaly, as the hierarchy of classes
![]() $D_\eta (\boldsymbol {\Sigma }^0_\xi )$
is proper, and this is witnessed by lightface sets. Still, the classes
$D_\eta (\boldsymbol {\Sigma }^0_\xi )$
is proper, and this is witnessed by lightface sets. Still, the classes
![]() $D_\eta (\Sigma ^0_\xi )$
are not as robust as the boldface ones. Louveau and Saint Raymond’s work in [Reference Louveau and Saint Raymond37] implies a weakening of Theorem 3.3 which is robust:
$D_\eta (\Sigma ^0_\xi )$
are not as robust as the boldface ones. Louveau and Saint Raymond’s work in [Reference Louveau and Saint Raymond37] implies a weakening of Theorem 3.3 which is robust:
 $$\begin{align*}\Delta^0_{\xi+1}(\Delta^1_1) = \bigcup_{\eta<\omega_1^{\text{ck}}} D_\eta(\Sigma^0_\xi)(\Delta^1_1), \end{align*}$$
$$\begin{align*}\Delta^0_{\xi+1}(\Delta^1_1) = \bigcup_{\eta<\omega_1^{\text{ck}}} D_\eta(\Sigma^0_\xi)(\Delta^1_1), \end{align*}$$
where for a class
![]() $\Gamma $
we let
$\Gamma $
we let
![]() $\Gamma (\Delta ^1_1) = \bigcup _{z\in \Delta ^1_1} \Gamma (z)$
. The class
$\Gamma (\Delta ^1_1) = \bigcup _{z\in \Delta ^1_1} \Gamma (z)$
. The class
![]() $D_\eta (\Sigma ^0_\xi )(\Delta ^1_1)$
depends only on the ordinal
$D_\eta (\Sigma ^0_\xi )(\Delta ^1_1)$
depends only on the ordinal
![]() $\eta $
and not on the choice of a
$\eta $
and not on the choice of a
![]() $\Delta ^1_1$
copy of
$\Delta ^1_1$
copy of
![]() $\eta $
; this is because any two
$\eta $
; this is because any two
![]() $\Delta ^1_1$
copies of
$\Delta ^1_1$
copies of
![]() $\eta $
are isomorphic by a
$\eta $
are isomorphic by a
![]() $\Delta ^1_1$
isomorphism.
$\Delta ^1_1$
isomorphism.
The standard definitions of the Borel classes
![]() $\boldsymbol {\Sigma }^0_\xi $
and
$\boldsymbol {\Sigma }^0_\xi $
and
![]() $\boldsymbol {\Delta }^0_\xi $
, as well as Definition 3.1, are, in the parlance of computability theory, static: sets in these classes are characterised by Boolean operations. Property TSP(4) of the true stages machinery allows us to view membership in a
$\boldsymbol {\Delta }^0_\xi $
, as well as Definition 3.1, are, in the parlance of computability theory, static: sets in these classes are characterised by Boolean operations. Property TSP(4) of the true stages machinery allows us to view membership in a
![]() $\Sigma ^0_{1+\alpha }$
set as the result of a dynamic process: to determine whether
$\Sigma ^0_{1+\alpha }$
set as the result of a dynamic process: to determine whether
![]() $x\in A$
, we search over the finite sequences
$x\in A$
, we search over the finite sequences
![]() $\sigma \prec _\alpha x$
, and we declare “yes” when we find such
$\sigma \prec _\alpha x$
, and we declare “yes” when we find such
![]() $\sigma $
enumerated into U.
$\sigma $
enumerated into U.
For the ambiguous classes, the prototypical dynamic decision process is given by Shoenfield’s “limit lemma” [Reference Shoenfield51], which states that a function
![]() $F\colon \mathbb N\to \mathbb N$
is
$F\colon \mathbb N\to \mathbb N$
is
![]() $\Delta ^0_2$
(equivalently, computable from the halting problem
$\Delta ^0_2$
(equivalently, computable from the halting problem
![]() $\emptyset '$
) if and only if it has a computable approximation: a computable function
$\emptyset '$
) if and only if it has a computable approximation: a computable function
![]() $f\colon \mathbb N^2\to \mathbb N$
such that for all n,
$f\colon \mathbb N^2\to \mathbb N$
such that for all n,
![]() $F(n)= \lim _s f(n,s)$
, the limit taken with respect to the discrete topology on
$F(n)= \lim _s f(n,s)$
, the limit taken with respect to the discrete topology on
![]() $\mathbb N$
. That is, for all n, for all but finitely many s,
$\mathbb N$
. That is, for all n, for all but finitely many s,
![]() $F(n) = f(n,s)$
. Each function
$F(n) = f(n,s)$
. Each function
![]() $n \mapsto f(n,s)$
is the “stage s guess” of the values of F.
$n \mapsto f(n,s)$
is the “stage s guess” of the values of F.
This can be extended to subsets of Baire space: a computable approximation of a function
![]() $F\colon \mathcal {N}\to \mathbb N$
is a computable function
$F\colon \mathcal {N}\to \mathbb N$
is a computable function
![]() $f\colon \omega ^{<\omega }\to \mathbb N$
such that for all
$f\colon \omega ^{<\omega }\to \mathbb N$
such that for all
![]() $x\in \mathcal {N}$
, for all but finitely many
$x\in \mathcal {N}$
, for all but finitely many
![]() $\sigma \prec x$
, we have
$\sigma \prec x$
, we have
![]() $F(x) = f(\sigma )$
. That is, the sequence
$F(x) = f(\sigma )$
. That is, the sequence
![]() $f(x\! \upharpoonright \!{0})$
,
$f(x\! \upharpoonright \!{0})$
,
![]() $f(x\! \upharpoonright \!{1}),\dots $
approximates
$f(x\! \upharpoonright \!{1}),\dots $
approximates
![]() $F(x)$
in the sense of Shoenfield. Shoenfield’s limit lemma relativises uniformly, and so it shows that a function
$F(x)$
in the sense of Shoenfield. Shoenfield’s limit lemma relativises uniformly, and so it shows that a function
![]() $F\colon \mathcal {N}\to \mathbb N$
has a computable approximation if and only if it is
$F\colon \mathcal {N}\to \mathbb N$
has a computable approximation if and only if it is
![]() $\Delta ^0_2$
-measurable. Using true stages, we can extend this further up the Borel hierarchy.
$\Delta ^0_2$
-measurable. Using true stages, we can extend this further up the Borel hierarchy.
Definition 3.5. Let
![]() $F\colon \mathcal {N}\to \mathbb N$
and let
$F\colon \mathcal {N}\to \mathbb N$
and let
![]() $\alpha <\omega _1^{\text {ck}}$
. An
$\alpha <\omega _1^{\text {ck}}$
. An
![]() $\alpha $
-approximation of F is a function
$\alpha $
-approximation of F is a function
![]() $f\colon \omega ^{<\omega }\to \mathbb N$
such that for all
$f\colon \omega ^{<\omega }\to \mathbb N$
such that for all
![]() $x\in \mathcal {N}$
,
$x\in \mathcal {N}$
,
(in the sense that for all but finitely many
![]() $\sigma \prec _\alpha x$
we have
$\sigma \prec _\alpha x$
we have
![]() $F(x) = f(\sigma )$
).
$F(x) = f(\sigma )$
).
The
![]() $\alpha $
-analogue of Shoenfield’s limit lemma is the following. Recall that for a lightface class
$\alpha $
-analogue of Shoenfield’s limit lemma is the following. Recall that for a lightface class
![]() $\Gamma $
, a function
$\Gamma $
, a function
![]() $F\colon \mathcal {N}\to \mathbb N$
is
$F\colon \mathcal {N}\to \mathbb N$
is
![]() $\Gamma $
-measurable if the sets
$\Gamma $
-measurable if the sets
![]() $F^{-1}\{n\}$
are in
$F^{-1}\{n\}$
are in
![]() $\Gamma $
, uniformly in n.
$\Gamma $
, uniformly in n.
Proposition 3.6. A function
![]() $F\colon \mathcal {N}\to \mathbb N$
is
$F\colon \mathcal {N}\to \mathbb N$
is
![]() $\Delta ^0_{1+\alpha +1}$
-measurable if and only if it has a computable
$\Delta ^0_{1+\alpha +1}$
-measurable if and only if it has a computable
![]() $\alpha $
-approximation.
$\alpha $
-approximation.
Proof In one direction, let f be a computable
![]() $\alpha $
-approximation of F. For
$\alpha $
-approximation of F. For
![]() $\sigma \in \omega ^{<\omega }$
, let
$\sigma \in \omega ^{<\omega }$
, let
![]() $|\sigma |_\alpha $
denote the height of
$|\sigma |_\alpha $
denote the height of
![]() $\sigma $
in the tree
$\sigma $
in the tree
![]() $(\omega ^{<\omega }, \preceq _{\alpha +1})$
. For
$(\omega ^{<\omega }, \preceq _{\alpha +1})$
. For
![]() $n,k<\omega $
, let
$n,k<\omega $
, let
These sets are uniformly
![]() $\Sigma ^0_{1+\alpha }$
. For each k,
$\Sigma ^0_{1+\alpha }$
. For each k,
![]() $\{A_{n,k}\,:\, n<\omega \}$
partitions
$\{A_{n,k}\,:\, n<\omega \}$
partitions
![]() $\mathcal {N}$
, so the sets
$\mathcal {N}$
, so the sets
![]() $A_{n,k}$
are in fact uniformly
$A_{n,k}$
are in fact uniformly
![]() $\Delta ^0_{1+\alpha }$
, so for all m,
$\Delta ^0_{1+\alpha }$
, so for all m,
![]() $\bigcap _{k\geqslant m} A_{n,k}$
is
$\bigcap _{k\geqslant m} A_{n,k}$
is
![]() $\Pi ^0_{1+\alpha }$
(again, uniformly). Now for all n,
$\Pi ^0_{1+\alpha }$
(again, uniformly). Now for all n,
![]() $F(x)=n$
if and only if
$F(x)=n$
if and only if
![]() $x\in A_{n,k}$
for all but finitely many k, so F is
$x\in A_{n,k}$
for all but finitely many k, so F is
![]() $\Sigma ^0_{1+\alpha +1}$
-measurable, which implies that it is
$\Sigma ^0_{1+\alpha +1}$
-measurable, which implies that it is
![]() $\Delta ^0_{1+\alpha +1}$
-measurable.
$\Delta ^0_{1+\alpha +1}$
-measurable.
In the other direction, suppose that
![]() $F\colon \mathcal {N}\to \mathbb N$
is
$F\colon \mathcal {N}\to \mathbb N$
is
![]() $\Delta ^0_{1+\alpha +1}$
-measurable. By TSP(4), which applies uniformly, there are uniformly c.e. sets
$\Delta ^0_{1+\alpha +1}$
-measurable. By TSP(4), which applies uniformly, there are uniformly c.e. sets
![]() $U_n\subseteq \omega ^{<\omega }$
such that for all
$U_n\subseteq \omega ^{<\omega }$
such that for all
![]() $x\in \mathcal {N}$
,
$x\in \mathcal {N}$
,
![]() $F(x)=n$
if and only if
$F(x)=n$
if and only if
![]() $x\in [U_n]^\prec _{\alpha +1}$
.
$x\in [U_n]^\prec _{\alpha +1}$
.
We may assume that:
-
(a) the sets
 $U_n$
are upwards closed in
$U_n$
are upwards closed in
 $(\omega ^{<\omega }, \preceq _{\alpha +1})$
;
$(\omega ^{<\omega }, \preceq _{\alpha +1})$
; -
(b) the sets
 $U_n$
are uniformly computable (rather than uniformly c.e.), and their union
$U_n$
are uniformly computable (rather than uniformly c.e.), and their union
 $\bigcup _n U_n$
is computable as well; and
$\bigcup _n U_n$
is computable as well; and -
(c) the sets
 $U_n$
are pairwise disjoint.
$U_n$
are pairwise disjoint.
This is a standard trick from computability theory, relying on the fact that the upwards closure of
![]() $U_n$
in
$U_n$
in
![]() $(\omega ^{<\omega },\preceq _{\alpha +1})$
generates the same
$(\omega ^{<\omega },\preceq _{\alpha +1})$
generates the same
![]() $\Sigma ^0_{1+\alpha +1}$
set. For each
$\Sigma ^0_{1+\alpha +1}$
set. For each
![]() $\tau \in \omega ^{<\omega }$
, we let
$\tau \in \omega ^{<\omega }$
, we let
![]() $s=|\tau |_{\alpha +1}$
be the height of
$s=|\tau |_{\alpha +1}$
be the height of
![]() $\tau $
in the tree
$\tau $
in the tree
![]() $(\omega ^{<\omega }, \preceq _{\alpha +1})$
. We then declare that
$(\omega ^{<\omega }, \preceq _{\alpha +1})$
. We then declare that
![]() $\tau $
belongs to the modified
$\tau $
belongs to the modified
![]() $U_n$
if
$U_n$
if
![]() $n<s$
, some
$n<s$
, some
![]() $\sigma \preceq _{\alpha +1}\tau $
is enumerated into
$\sigma \preceq _{\alpha +1}\tau $
is enumerated into
![]() $U_n$
by stage s, and this does not hold for any
$U_n$
by stage s, and this does not hold for any
![]() $m<n$
.Footnote
2
$m<n$
.Footnote
2
Having guaranteed properties (a)–(c) above, we define
![]() $f(\sigma )=n$
for all
$f(\sigma )=n$
for all
![]() $\sigma \in U_n$
, and
$\sigma \in U_n$
, and
![]() $f(\sigma )=0$
if
$f(\sigma )=0$
if
![]() $\sigma \notin \bigcup _n U_n$
. Property (b) implies that f is computable. We show that f is an
$\sigma \notin \bigcup _n U_n$
. Property (b) implies that f is computable. We show that f is an
![]() $\alpha $
-approximation of F. Let
$\alpha $
-approximation of F. Let
![]() $x\in \mathcal {N}$
; let
$x\in \mathcal {N}$
; let
![]() $n = F(x)$
. There is some
$n = F(x)$
. There is some
![]() $\sigma \prec _{\alpha +1} x$
in
$\sigma \prec _{\alpha +1} x$
in
![]() $U_n$
. Let
$U_n$
. Let
![]() $\tau $
be such that
$\tau $
be such that
![]() $\sigma \preceq _\alpha \tau \prec _\alpha x$
. By (♣),
$\sigma \preceq _\alpha \tau \prec _\alpha x$
. By (♣),
![]() $\sigma \preceq _{\alpha +1} \tau $
. Since
$\sigma \preceq _{\alpha +1} \tau $
. Since
![]() $U_n$
is
$U_n$
is
![]() $\preceq _{\alpha +1}$
-upwards closed,
$\preceq _{\alpha +1}$
-upwards closed,
![]() $\tau \in U_n$
, so
$\tau \in U_n$
, so
![]() $f(\tau )=n$
.
$f(\tau )=n$
.
Remark 3.7. Proposition 3.6 is inherently effective. In the language of effective topology, it says that a function
![]() $F\colon \mathcal {N}\to \mathbb N$
has a computable
$F\colon \mathcal {N}\to \mathbb N$
has a computable
![]() $\alpha $
-approximation if and only if it is effectively continuous with respect to the
$\alpha $
-approximation if and only if it is effectively continuous with respect to the
![]() $(\emptyset ,\alpha +1)$
-topology. One could imagine that this is just the effective version of the following: a function
$(\emptyset ,\alpha +1)$
-topology. One could imagine that this is just the effective version of the following: a function
![]() $F\colon \mathcal {N}\to \mathbb N$
has an
$F\colon \mathcal {N}\to \mathbb N$
has an
![]() $\alpha $
-approximation if and only if it is continuous with respect to the
$\alpha $
-approximation if and only if it is continuous with respect to the
![]() $(\emptyset ,\alpha +1)$
-topology. The proof above gives the right-to-left implication. However, the “easier” direction may fail: if f is an
$(\emptyset ,\alpha +1)$
-topology. The proof above gives the right-to-left implication. However, the “easier” direction may fail: if f is an
![]() $\alpha $
-approximation of F, then F is
$\alpha $
-approximation of F, then F is
![]() $\Delta ^0_{1+\alpha +1}(f)$
-measurable; this does not imply
$\Delta ^0_{1+\alpha +1}(f)$
-measurable; this does not imply
![]() $(\emptyset ,\alpha +1)$
-continuity.
$(\emptyset ,\alpha +1)$
-continuity.
We note, though, that the proof of Theorem 3.3 only uses the “harder” direction. Thus, we could use the machinery to give a direct proof of Theorem 3.2 without passing through Theorem 3.3. This is the path we take with Wadge’s theorem below.
Toward a proof of Theorem 3.3, we give a dynamic description of the class
![]() $D_\eta (\Sigma ^0_{1+\alpha })$
. Let A be the
$D_\eta (\Sigma ^0_{1+\alpha })$
. Let A be the
![]() $D_\eta (\Sigma ^0_{1+\alpha })$
set defined from the increasing sequence
$D_\eta (\Sigma ^0_{1+\alpha })$
set defined from the increasing sequence
![]() ${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
. After taking
${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
. After taking
![]() $\alpha $
jumps, the sets
$\alpha $
jumps, the sets
![]() $A_i$
can be thought of as being “c.e.” (TSP(4)). The dynamic process we envision for deciding if
$A_i$
can be thought of as being “c.e.” (TSP(4)). The dynamic process we envision for deciding if
![]() $x\in A$
is the following. We start by guessing that
$x\in A$
is the following. We start by guessing that
![]() $x\notin A$
. Once we see that
$x\notin A$
. Once we see that
![]() $x\in \bigcup _{i<\eta } A_{i}$
, at each stage s, we find the least
$x\in \bigcup _{i<\eta } A_{i}$
, at each stage s, we find the least
![]() $i<\eta $
for which
$i<\eta $
for which
![]() $x\in A_i$
, and we guess that
$x\in A_i$
, and we guess that
![]() $x\in A$
if and only if the parity
$x\in A$
if and only if the parity
![]() $(i)\ne $
parity
$(i)\ne $
parity
![]() $(\eta )$
. In fact, this is a particular kind of an
$(\eta )$
. In fact, this is a particular kind of an
![]() $\alpha $
-approximation.
$\alpha $
-approximation.
Proposition 3.8. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\eta \geqslant 1$
be computable ordinals. A set
$\eta \geqslant 1$
be computable ordinals. A set
![]() $A\subseteq \mathcal {N}$
is in
$A\subseteq \mathcal {N}$
is in
![]() $D_\eta (\Sigma ^0_{1+\alpha })$
if and only if its characteristic function
$D_\eta (\Sigma ^0_{1+\alpha })$
if and only if its characteristic function
![]() $1_A$
has a computable
$1_A$
has a computable
![]() $\alpha $
-approximation f for which is there is a computable “witness” function
$\alpha $
-approximation f for which is there is a computable “witness” function
![]() $o\colon \omega ^{<\omega }\to \eta +1$
satisfying:
$o\colon \omega ^{<\omega }\to \eta +1$
satisfying:
-
(i) If
 $\sigma \preceq _\alpha \tau $
then
$\sigma \preceq _\alpha \tau $
then
 $o(\tau )\leqslant o(\sigma )$
.
$o(\tau )\leqslant o(\sigma )$
. -
(ii) If
 $\sigma \preceq _\alpha \tau $
and
$\sigma \preceq _\alpha \tau $
and
 $f(\tau )\ne f(\sigma )$
then
$f(\tau )\ne f(\sigma )$
then
 $o(\tau )< o(\sigma )$
.
$o(\tau )< o(\sigma )$
. -
(iii) If
 $o(\sigma )=\eta $
then
$o(\sigma )=\eta $
then
 $f(\sigma )=0$
.
$f(\sigma )=0$
.
This notion of a “witness” for the convergence of an approximation is widely used for computable approximations of functions
![]() $F\colon \mathbb N\to \mathbb N$
(see, for example, [Reference Downey and Greenberg12, Chapter 2]). The idea is that the well-foundedness of
$F\colon \mathbb N\to \mathbb N$
(see, for example, [Reference Downey and Greenberg12, Chapter 2]). The idea is that the well-foundedness of
![]() $\eta +1$
guarantees that the sequence
$\eta +1$
guarantees that the sequence
![]() ${\left \langle {f(\sigma )}\right \rangle }_{\sigma \prec _\alpha x}$
eventually stabilises, i.e., that
${\left \langle {f(\sigma )}\right \rangle }_{\sigma \prec _\alpha x}$
eventually stabilises, i.e., that
![]() ${f}$
indeed
${f}$
indeed
![]() $\alpha $
-converges to a limit F. In general, the more “mind-changes” the approximation has, the more complicated the function F can be. The longer
$\alpha $
-converges to a limit F. In general, the more “mind-changes” the approximation has, the more complicated the function F can be. The longer
![]() $\eta $
is, the “more room” we have for mind-changes.
$\eta $
is, the “more room” we have for mind-changes.
Proof In one direction, let A be a
![]() $D_\eta (\Sigma ^0_{1+\alpha })$
set; let
$D_\eta (\Sigma ^0_{1+\alpha })$
set; let
![]() ${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
be the sequence of uniformly
${\left \langle {A_{i}}\right \rangle }_{i<\eta }$
be the sequence of uniformly
![]() $\Sigma ^0_{1+\alpha }$
sets used to define A. For uniformity of notation, let
$\Sigma ^0_{1+\alpha }$
sets used to define A. For uniformity of notation, let
![]() $A_\eta = \mathcal {N}$
. Then
$A_\eta = \mathcal {N}$
. Then
![]() ${\left \langle {A_i}\right \rangle }_{i\leqslant \eta }$
is increasing and uniformly
${\left \langle {A_i}\right \rangle }_{i\leqslant \eta }$
is increasing and uniformly
![]() $\Sigma ^0_{1+\alpha }$
, and
$\Sigma ^0_{1+\alpha }$
, and
![]() $x\in A$
if and only if parity
$x\in A$
if and only if parity
![]() $(i)\ne $
parity
$(i)\ne $
parity
![]() $(\eta )$
for the least i such that
$(\eta )$
for the least i such that
![]() $x\in A_i$
.
$x\in A_i$
.
By TSP(4), let
![]() $U_i$
be a sequence of uniformly c.e. subsets of
$U_i$
be a sequence of uniformly c.e. subsets of
![]() $\omega ^{<\omega }$
such that
$\omega ^{<\omega }$
such that
![]() $A_i = [U_i]^\prec _\alpha $
. As in the proof of Proposition 3.6, we may assume that the sets
$A_i = [U_i]^\prec _\alpha $
. As in the proof of Proposition 3.6, we may assume that the sets
![]() $U_i$
are uniformly computable, and each is upwards closed in
$U_i$
are uniformly computable, and each is upwards closed in
![]() $(\omega ^{<\omega },\preceq _\alpha )$
. We may take
$(\omega ^{<\omega },\preceq _\alpha )$
. We may take
![]() $U_\eta = \omega ^{<\omega }$
.
$U_\eta = \omega ^{<\omega }$
.
Recall that we are working with a computable copy of
![]() $\eta $
, i.e., a computable well-ordering
$\eta $
, i.e., a computable well-ordering
![]() $<^*$
of
$<^*$
of
![]() $\mathbb N$
such that
$\mathbb N$
such that
![]() $(\mathbb N, <^*)\cong \eta $
. Let
$(\mathbb N, <^*)\cong \eta $
. Let
![]() $n\mapsto i_n$
be the isomorphism. For each
$n\mapsto i_n$
be the isomorphism. For each
![]() $\sigma \in \omega ^{<\omega }$
, let
$\sigma \in \omega ^{<\omega }$
, let
![]() $O(\sigma ) = \{\eta \}\cup \left \{ i_n \,:\, n<|\sigma | \right \}$
(more thematically, we should take
$O(\sigma ) = \{\eta \}\cup \left \{ i_n \,:\, n<|\sigma | \right \}$
(more thematically, we should take
![]() $n<|\sigma |_\alpha $
, where as above
$n<|\sigma |_\alpha $
, where as above
![]() $|\sigma |_\alpha $
is the height of
$|\sigma |_\alpha $
is the height of
![]() $\sigma $
in the tree
$\sigma $
in the tree
![]() $(\omega ^{<\omega },\preceq _\alpha )$
). So
$(\omega ^{<\omega },\preceq _\alpha )$
). So
![]() $O(\sigma )$
is a finite subset of
$O(\sigma )$
is a finite subset of
![]() $\eta +1$
, the map
$\eta +1$
, the map
![]() $\sigma \mapsto O(\sigma )$
is computable,
$\sigma \mapsto O(\sigma )$
is computable,
![]() $O(\sigma )\subseteq O(\tau )$
if
$O(\sigma )\subseteq O(\tau )$
if
![]() $\sigma \preceq _\alpha \tau $
,
$\sigma \preceq _\alpha \tau $
,
![]() $\bigcup _{\sigma \prec _\alpha x} O(\sigma ) = \eta +1$
for all
$\bigcup _{\sigma \prec _\alpha x} O(\sigma ) = \eta +1$
for all
![]() $x\in \mathcal {N}$
, and
$x\in \mathcal {N}$
, and
![]() $\eta \in O(\sigma )$
for all
$\eta \in O(\sigma )$
for all
![]() $\sigma $
.
$\sigma $
.
Define
![]() $f\colon \omega ^{<\omega }\to \{0,1\}$
and
$f\colon \omega ^{<\omega }\to \{0,1\}$
and
![]() $o\colon \omega ^{<\omega }\to \eta +1$
as follows. Given
$o\colon \omega ^{<\omega }\to \eta +1$
as follows. Given
![]() $\sigma \in \omega ^{<\omega }$
, let
$\sigma \in \omega ^{<\omega }$
, let
![]() $o(\sigma )$
be the least
$o(\sigma )$
be the least
![]() $i\in O(\sigma )$
(in the ordering of
$i\in O(\sigma )$
(in the ordering of
![]() $\eta $
) such that
$\eta $
) such that
![]() $\sigma \in U_i$
; let
$\sigma \in U_i$
; let
![]() $f(\sigma )=1$
if parity
$f(\sigma )=1$
if parity
![]() $(o(\sigma ))\ne $
parity
$(o(\sigma ))\ne $
parity
![]() $(\eta )$
,
$(\eta )$
,
![]() $0$
otherwise.
$0$
otherwise.
Since we arranged for the sequences
![]() ${\left \langle {U_i}\right \rangle }$
to be computable, the functions o and f are computable. We verify that the required conditions hold. For (i), let
${\left \langle {U_i}\right \rangle }$
to be computable, the functions o and f are computable. We verify that the required conditions hold. For (i), let
![]() $\sigma \preceq _\alpha \tau $
. Since each
$\sigma \preceq _\alpha \tau $
. Since each
![]() $U_i$
is upwards closed in
$U_i$
is upwards closed in
![]() $\preceq _\alpha $
, we have
$\preceq _\alpha $
, we have
![]() $\tau \in U_{o(\sigma )}$
; since
$\tau \in U_{o(\sigma )}$
; since
![]() $o(\sigma )\in O(\tau )$
, (i) holds. (ii) holds since
$o(\sigma )\in O(\tau )$
, (i) holds. (ii) holds since
![]() $f(\sigma )$
is determined by
$f(\sigma )$
is determined by
![]() $o(\sigma )$
, and similarly for (iii). Finally, for each
$o(\sigma )$
, and similarly for (iii). Finally, for each
![]() $x\in \mathcal {N}$
,
$x\in \mathcal {N}$
,
![]() $1_A(x) = \lim _{\sigma \prec _\alpha x} f(\sigma )$
because for almost all
$1_A(x) = \lim _{\sigma \prec _\alpha x} f(\sigma )$
because for almost all
![]() $\sigma \prec _\alpha x$
we have
$\sigma \prec _\alpha x$
we have
![]() $o(\sigma ) = o(x) = \min \{i<\eta \,:\, x\in A_i\}$
.
$o(\sigma ) = o(x) = \min \{i<\eta \,:\, x\in A_i\}$
.
In the other direction, let f be an
![]() $\alpha $
-computable approximation of the characteristic function
$\alpha $
-computable approximation of the characteristic function
![]() $1_A$
of A, with a witnessing function o as described. We would like to let
$1_A$
of A, with a witnessing function o as described. We would like to let
![]() $U_i = \left \{ \sigma \in \omega ^{<\omega } \,:\, o(\sigma )\leqslant i \right \}$
and
$U_i = \left \{ \sigma \in \omega ^{<\omega } \,:\, o(\sigma )\leqslant i \right \}$
and
![]() $A_i = [U]^\prec _\alpha $
. This would work if
$A_i = [U]^\prec _\alpha $
. This would work if
![]() $f(\sigma )=1$
if and only if parity
$f(\sigma )=1$
if and only if parity
![]() $(o(\sigma ))\ne $
parity
$(o(\sigma ))\ne $
parity
![]() $(\eta )$
. This, however, is only guaranteed when
$(\eta )$
. This, however, is only guaranteed when
![]() $o(\sigma )=\eta $
(this is condition (iii)). So it remains to show that we can modify o to get a witness
$o(\sigma )=\eta $
(this is condition (iii)). So it remains to show that we can modify o to get a witness
![]() $\tilde o\colon \omega ^{<\omega }\to \eta +1$
satisfying (i)–(iii) and also satisfying
$\tilde o\colon \omega ^{<\omega }\to \eta +1$
satisfying (i)–(iii) and also satisfying
![]() $f(\sigma )=1$
if and only if parity
$f(\sigma )=1$
if and only if parity
![]() $(\tilde o(\sigma ))\ne $
parity
$(\tilde o(\sigma ))\ne $
parity
![]() $(\eta )$
.
$(\eta )$
.
This is easily done by setting
![]() $\tilde o(\sigma )$
to be either
$\tilde o(\sigma )$
to be either
![]() $o(\sigma )$
or
$o(\sigma )$
or
![]() $o(\sigma )+1$
, the choice determined by
$o(\sigma )+1$
, the choice determined by
![]() $f(\sigma )$
and the parity of the ordinals. As mentioned, (iii) for o shows that if
$f(\sigma )$
and the parity of the ordinals. As mentioned, (iii) for o shows that if
![]() $o(\sigma ) = \eta $
then
$o(\sigma ) = \eta $
then
![]() $\tilde o(\sigma )=\eta $
as well; we never need to choose the value
$\tilde o(\sigma )=\eta $
as well; we never need to choose the value
![]() $\eta +1$
. We need to verify (i) for
$\eta +1$
. We need to verify (i) for
![]() $\tilde o$
(and then (ii) follows). Suppose that
$\tilde o$
(and then (ii) follows). Suppose that
![]() $\sigma \preceq _\alpha \tau $
. Since
$\sigma \preceq _\alpha \tau $
. Since
![]() $o(\tau )\leqslant o(\sigma )$
, we would only have a problem if
$o(\tau )\leqslant o(\sigma )$
, we would only have a problem if
![]() $o(\tau ) = o(\sigma ) = i$
but
$o(\tau ) = o(\sigma ) = i$
but
![]() $\tilde o(\sigma ) = i+1$
while
$\tilde o(\sigma ) = i+1$
while
![]() $\tilde o(\tau ) = i$
. But this implies that
$\tilde o(\tau ) = i$
. But this implies that
![]() $f(\sigma )\ne f(\tau )$
, which is impossible since o satisfies (ii).
$f(\sigma )\ne f(\tau )$
, which is impossible since o satisfies (ii).
Remark 3.9. Ershov showed that a function
![]() $F\colon \mathbb N\to \mathbb N$
is
$F\colon \mathbb N\to \mathbb N$
is
![]() $D_\eta (\Sigma ^0_1)$
-measurable if and only if it has a computable approximation f with a
$D_\eta (\Sigma ^0_1)$
-measurable if and only if it has a computable approximation f with a
![]() $<\eta $
-witness: a computable function
$<\eta $
-witness: a computable function
![]() $o\colon \mathbb N^2\to \eta $
such that
$o\colon \mathbb N^2\to \eta $
such that
![]() $o(n,s)\geqslant o(n,t)$
when
$o(n,s)\geqslant o(n,t)$
when
![]() $t\geqslant s$
and
$t\geqslant s$
and
![]() $o(n,s)>o(n,t)$
when in addition
$o(n,s)>o(n,t)$
when in addition
![]() $f(n,s)\ne f(n,t)$
. Such functions are called
$f(n,s)\ne f(n,t)$
. Such functions are called
![]() $\eta $
-computably approximable in [Reference Downey and Greenberg12]. In particular, a set
$\eta $
-computably approximable in [Reference Downey and Greenberg12]. In particular, a set
![]() $A\subseteq \mathbb N$
is in Ershov’s ambiguous class
$A\subseteq \mathbb N$
is in Ershov’s ambiguous class
![]() $\Delta ^{-1}_\eta $
(i.e., it is both
$\Delta ^{-1}_\eta $
(i.e., it is both
![]() $D_\eta (\Sigma ^0_1)$
and co-
$D_\eta (\Sigma ^0_1)$
and co-
![]() $D_\eta (\Sigma ^0_1)$
) if and only if its characteristic function is
$D_\eta (\Sigma ^0_1)$
) if and only if its characteristic function is
![]() $\eta $
-c.a. The idea is that for each n, since we know that
$\eta $
-c.a. The idea is that for each n, since we know that
![]() $f(n)$
is defined, we can wait for an approximation of one the sets
$f(n)$
is defined, we can wait for an approximation of one the sets
![]() $F^{-1}\{m\}$
to give us an ordinal below
$F^{-1}\{m\}$
to give us an ordinal below
![]() $\eta $
, and then start our approximation from that point.
$\eta $
, and then start our approximation from that point.
We can similarly define a notion of an
![]() $<\eta $
-witness for a computable
$<\eta $
-witness for a computable
![]() $\alpha $
-approximation of a
$\alpha $
-approximation of a
![]() $\Delta ^0_{1+\alpha +1}$
-measurable function
$\Delta ^0_{1+\alpha +1}$
-measurable function
![]() $F\colon \mathcal {N}\to \mathbb N$
: a function o as in Proposition 3.8 but which takes values below
$F\colon \mathcal {N}\to \mathbb N$
: a function o as in Proposition 3.8 but which takes values below
![]() $\eta $
; the value
$\eta $
; the value
![]() $\eta $
is not allowed, and so condition (iii) is removed.
$\eta $
is not allowed, and so condition (iii) is removed.
We would then hope that every
![]() $D_\eta (\Sigma ^0_1)$
-measurable function
$D_\eta (\Sigma ^0_1)$
-measurable function
![]() $F\colon \mathcal {N}\to \mathbb N$
has a computable
$F\colon \mathcal {N}\to \mathbb N$
has a computable
![]() $\alpha $
-approximation with such a witness o. This is almost the case; since we have to wait until we see an ordinal drop, the function o will not be defined on all of
$\alpha $
-approximation with such a witness o. This is almost the case; since we have to wait until we see an ordinal drop, the function o will not be defined on all of
![]() $\omega ^{<\omega }$
but rather on a computable subset of
$\omega ^{<\omega }$
but rather on a computable subset of
![]() $\omega ^{<\omega }$
which is dense and upwards-closed in
$\omega ^{<\omega }$
which is dense and upwards-closed in
![]() $(\omega ^{<\omega },\prec _\alpha )$
. We study such functions in greater detail in [Reference Day, Greenberg, Harrison-Trainor and Turetsky8].
$(\omega ^{<\omega },\prec _\alpha )$
. We study such functions in greater detail in [Reference Day, Greenberg, Harrison-Trainor and Turetsky8].
We can now prove the effective Hausdorff–Kuratowski theorem.
Proof of Theorem 3.3
By Propositions 3.6 and 3.8, it suffices to show: if
![]() $f\colon \omega ^{<\omega }\to \mathbb N$
is a computable
$f\colon \omega ^{<\omega }\to \mathbb N$
is a computable
![]() $\alpha $
-approximation of a function
$\alpha $
-approximation of a function
![]() $F\colon \mathcal {N}\to \mathbb N$
, then there is some computable well-ordering
$F\colon \mathcal {N}\to \mathbb N$
, then there is some computable well-ordering
![]() $\eta $
and some computable witness function
$\eta $
and some computable witness function
![]() $o\colon \omega ^{<\omega }\to \eta $
satisfying (i) and (ii) of Proposition 3.8. By applying this to
$o\colon \omega ^{<\omega }\to \eta $
satisfying (i) and (ii) of Proposition 3.8. By applying this to
![]() $F = 1_A$
, it will follow that A is
$F = 1_A$
, it will follow that A is
![]() $D_{\eta +1}(\Sigma ^0_\alpha )$
(since o never takes value
$D_{\eta +1}(\Sigma ^0_\alpha )$
(since o never takes value
![]() $\eta $
, property (iii) is irrelevant).
$\eta $
, property (iii) is irrelevant).
Let
![]() $T\subset \omega ^{<\omega }$
consist of the empty sequence, together with the finite sequences
$T\subset \omega ^{<\omega }$
consist of the empty sequence, together with the finite sequences
![]() $\sigma $
for which
$\sigma $
for which
![]() $f(\sigma )\ne f(\sigma ^-)$
, where
$f(\sigma )\ne f(\sigma ^-)$
, where
![]() $\sigma ^-$
is the immediate predecessor of
$\sigma ^-$
is the immediate predecessor of
![]() $\sigma $
on the tree
$\sigma $
on the tree
![]() $(\omega ^{<\omega },\preceq _\alpha )$
. As a subset of that tree,
$(\omega ^{<\omega },\preceq _\alpha )$
. As a subset of that tree,
![]() $(T,\preceq _\alpha )$
is a tree as well. It is well-founded: if
$(T,\preceq _\alpha )$
is a tree as well. It is well-founded: if
![]() ${\left \langle {\sigma _i}\right \rangle }_{i<\omega }$
is an infinite path in T, then by TSP(1) and TSP(3),
${\left \langle {\sigma _i}\right \rangle }_{i<\omega }$
is an infinite path in T, then by TSP(1) and TSP(3),
![]() $x= \bigcup _i \sigma _i$
is an element of Baire space and
$x= \bigcup _i \sigma _i$
is an element of Baire space and
![]() $\sigma _i\prec _\alpha x$
for all i; but then
$\sigma _i\prec _\alpha x$
for all i; but then
![]() ${\left \langle {f(\sigma )}\right \rangle }_{\sigma \prec _\alpha x}$
does not stabilise to
${\left \langle {f(\sigma )}\right \rangle }_{\sigma \prec _\alpha x}$
does not stabilise to
![]() $F(x)$
, contrary to the assumption that f is an
$F(x)$
, contrary to the assumption that f is an
![]() $\alpha $
-approximation of F.
$\alpha $
-approximation of F.
Now let
![]() $\eta $
be the Kleene–Brouwer ordering of T (also known as the Lusin–Sierpiński ordering [Reference Brouwer5, Reference Kleene26, Reference Lusin and Sierpiński39]; see [Reference Moschovakis44, Theorem 4A.4]). The identity function is a computable rank function
$\eta $
be the Kleene–Brouwer ordering of T (also known as the Lusin–Sierpiński ordering [Reference Brouwer5, Reference Kleene26, Reference Lusin and Sierpiński39]; see [Reference Moschovakis44, Theorem 4A.4]). The identity function is a computable rank function
![]() $r\colon T\to \eta $
. Extend r to a function
$r\colon T\to \eta $
. Extend r to a function
![]() $o\colon \omega ^{<\omega }\to \eta $
by letting
$o\colon \omega ^{<\omega }\to \eta $
by letting
![]() $o(\tau ) = r(\sigma )$
where
$o(\tau ) = r(\sigma )$
where
![]() $\sigma $
is the longest
$\sigma $
is the longest
![]() $\preceq _\alpha $
-predecessor of
$\preceq _\alpha $
-predecessor of
![]() $\tau $
which is on T.
$\tau $
which is on T.
3.2 Wadge’s theorem
Let
![]() $\lambda $
be a countable limit ordinal. Wadge described how to construct all sets in the class
$\lambda $
be a countable limit ordinal. Wadge described how to construct all sets in the class
![]() $\boldsymbol {\Delta }^0_\lambda $
starting from the sets in
$\boldsymbol {\Delta }^0_\lambda $
starting from the sets in
![]() $\boldsymbol {\Delta }^0_{<\lambda }$
and closing under the operation of taking separated unions.
$\boldsymbol {\Delta }^0_{<\lambda }$
and closing under the operation of taking separated unions.
Definition 3.10. A countable sequence of sets
![]() $(A_n)_{n \in \omega }$
is
$(A_n)_{n \in \omega }$
is
![]() $\boldsymbol {\Sigma }^0_\xi $
-separated if there is a sequence
$\boldsymbol {\Sigma }^0_\xi $
-separated if there is a sequence
![]() $(U_n)_{n \in \omega }$
of pairwise disjoint
$(U_n)_{n \in \omega }$
of pairwise disjoint
![]() $\boldsymbol {\Sigma }^0_\xi $
sets with
$\boldsymbol {\Sigma }^0_\xi $
sets with
![]() $A_n \subseteq U_n$
for all n.
$A_n \subseteq U_n$
for all n.
Theorem 3.11 (Wadge).
Let
![]() $\lambda $
be a countable limit ordinal. The class
$\lambda $
be a countable limit ordinal. The class
![]() $\boldsymbol {\Delta }^0_\lambda $
is the smallest collection of sets which:
$\boldsymbol {\Delta }^0_\lambda $
is the smallest collection of sets which:
-
• contains
 $\boldsymbol {\Sigma }^0_\xi $
, for all
$\boldsymbol {\Sigma }^0_\xi $
, for all
 $\xi < \lambda $
; and
$\xi < \lambda $
; and -
• is closed under unions of
 $\boldsymbol {\Sigma }^0_\xi $
-separated sequences, for all
$\boldsymbol {\Sigma }^0_\xi $
-separated sequences, for all
 $\xi < \lambda $
.
$\xi < \lambda $
.
Remark 3.12. Wadge stated his theorem in terms of partitioned unions, in which the pairwise disjoint
![]() $\boldsymbol {\Sigma }^0_\xi $
sets of Definition 3.10 are required to form a partition of
$\boldsymbol {\Sigma }^0_\xi $
sets of Definition 3.10 are required to form a partition of
![]() $\mathcal {N}$
. Every
$\mathcal {N}$
. Every
![]() $\boldsymbol {\Sigma }^0_\xi $
-separated union is of course a
$\boldsymbol {\Sigma }^0_\xi $
-separated union is of course a
![]() $\boldsymbol {\Sigma }^0_{\xi +1}$
-partitioned union, so for Wadge’s theorem we may use either notion. The difference between separated and partitioned unions is important in the analysis of all Borel Wadge classes.
$\boldsymbol {\Sigma }^0_{\xi +1}$
-partitioned union, so for Wadge’s theorem we may use either notion. The difference between separated and partitioned unions is important in the analysis of all Borel Wadge classes.
For our proof of Theorem 3.11, we require one last property of the true stages machinery. As observed above, this property is a special feature of the development of the machinery in [Reference Greenberg and Turetsky16]. As with TSP(6), it reflects the fact that for limit
![]() $\lambda $
,
$\lambda $
,
![]() $x^{(\lambda )}\equiv _{\mathrm{T}} \bigoplus _{\alpha <\lambda }x^{(\alpha )}$
. Recall the notation introduced in the proof of Proposition 3.6:
$x^{(\lambda )}\equiv _{\mathrm{T}} \bigoplus _{\alpha <\lambda }x^{(\alpha )}$
. Recall the notation introduced in the proof of Proposition 3.6:
![]() $|\sigma |_\alpha $
is the height of
$|\sigma |_\alpha $
is the height of
![]() $\sigma $
in the tree
$\sigma $
in the tree
![]() $(\omega ^{<\omega },\preceq _\alpha )$
.
$(\omega ^{<\omega },\preceq _\alpha )$
.
-
TSP(9): Let
 $\lambda < \omega _1^{\text {ck}}$
be computable and limit. There is a computable and increasing sequence
$\lambda < \omega _1^{\text {ck}}$
be computable and limit. There is a computable and increasing sequence
 ${\left \langle {\lambda _k}\right \rangle }$
, cofinal in
${\left \langle {\lambda _k}\right \rangle }$
, cofinal in
 $\lambda $
, such that for all
$\lambda $
, such that for all
 $\sigma \in \omega ^{<\omega }$
, letting
$\sigma \in \omega ^{<\omega }$
, letting
 $k = |\sigma |_\lambda $
, then
$k = |\sigma |_\lambda $
, then
 $|\sigma |_{\lambda _k} = k$
, and for all
$|\sigma |_{\lambda _k} = k$
, and for all
 $\tau \in \omega ^{\leqslant \omega }$
,
$\tau \in \omega ^{\leqslant \omega }$
,  $$\begin{align*}\sigma\preceq_\lambda \tau \,\,\,\Longleftrightarrow\,\,\, \sigma\preceq_{\lambda_k} \tau. \end{align*}$$
$$\begin{align*}\sigma\preceq_\lambda \tau \,\,\,\Longleftrightarrow\,\,\, \sigma\preceq_{\lambda_k} \tau. \end{align*}$$
Proof of Theorem 3.11
Let
![]() $\mathcal {C}$
be the smallest collection of sets with the above closure properties. An induction shows that
$\mathcal {C}$
be the smallest collection of sets with the above closure properties. An induction shows that
![]() $\mathcal {C}\subseteq \boldsymbol {\Delta }^0_\lambda $
, so we will show the converse: given an
$\mathcal {C}\subseteq \boldsymbol {\Delta }^0_\lambda $
, so we will show the converse: given an
![]() $A \in \boldsymbol {\Delta }^0_\lambda $
, we will demonstrate that
$A \in \boldsymbol {\Delta }^0_\lambda $
, we will demonstrate that
![]() $A \in \mathcal {C}$
. By working relative to an appropriate oracle, we may assume that
$A \in \mathcal {C}$
. By working relative to an appropriate oracle, we may assume that
![]() $\lambda < \omega _1^{\text {ck}}$
and
$\lambda < \omega _1^{\text {ck}}$
and
![]() $A \in \Delta ^0_\lambda $
.
$A \in \Delta ^0_\lambda $
.
Since
![]() $\lambda = 1+\lambda $
, TSP(4) gives us two c.e. sets
$\lambda = 1+\lambda $
, TSP(4) gives us two c.e. sets
![]() $W_0$
and
$W_0$
and
![]() $W_1$
such that
$W_1$
such that
![]() ${A = [W_1]^\prec _\lambda }$
and
${A = [W_1]^\prec _\lambda }$
and
![]() $A^\complement = \mathcal {N}\setminus A = [W_0]^\prec _\lambda $
. As in previous proofs, we may assume that
$A^\complement = \mathcal {N}\setminus A = [W_0]^\prec _\lambda $
. As in previous proofs, we may assume that
![]() $W_0$
and
$W_0$
and
![]() $W_1$
are disjoint and upwards closed in
$W_1$
are disjoint and upwards closed in
![]() $(\omega ^{<\omega },\preceq _\lambda )$
.
$(\omega ^{<\omega },\preceq _\lambda )$
.
Let
![]() $T = \omega ^{<\omega }\setminus (W_0 \cup W_1)$
. Then
$T = \omega ^{<\omega }\setminus (W_0 \cup W_1)$
. Then
![]() $(T,\preceq _\lambda )$
is a subtree of
$(T,\preceq _\lambda )$
is a subtree of
![]() $(\omega ^{<\omega },\preceq _\lambda )$
. Further, since
$(\omega ^{<\omega },\preceq _\lambda )$
. Further, since
![]() $[W_0]^\prec _\lambda \cup [W_1]^\prec _\lambda = \mathcal {N}$
, T is well-founded (as in the proof of Theorem 3.3, this uses TSP(1) and TSP(3)). Let
$[W_0]^\prec _\lambda \cup [W_1]^\prec _\lambda = \mathcal {N}$
, T is well-founded (as in the proof of Theorem 3.3, this uses TSP(1) and TSP(3)). Let
![]() $r\colon T\to \omega _1$
be a rank function for T.
$r\colon T\to \omega _1$
be a rank function for T.
We modify r to obtain a function
![]() $s\colon \omega ^{<\omega }\to \omega _1$
as follows:
$s\colon \omega ^{<\omega }\to \omega _1$
as follows:
 $$\begin{align*}s(\sigma) = \begin{cases} r(\sigma)+1, & \text{if } {\sigma \in T}, \\ 0, & \text{if } {\sigma \not \in T}. \end{cases} \end{align*}$$
$$\begin{align*}s(\sigma) = \begin{cases} r(\sigma)+1, & \text{if } {\sigma \in T}, \\ 0, & \text{if } {\sigma \not \in T}. \end{cases} \end{align*}$$
For each
![]() $\sigma \in \omega ^{<\omega }$
let
$\sigma \in \omega ^{<\omega }$
let
![]() $A_\sigma = A\cap [\sigma ]^\prec _\lambda $
. By induction on
$A_\sigma = A\cap [\sigma ]^\prec _\lambda $
. By induction on
![]() $s(\sigma )$
, we will show that
$s(\sigma )$
, we will show that
![]() $A_\sigma \in \mathcal {C}$
. The result will then follow since
$A_\sigma \in \mathcal {C}$
. The result will then follow since
![]() $A = A_{{\left \langle {}\right \rangle }}$
. Let
$A = A_{{\left \langle {}\right \rangle }}$
. Let
![]() ${\left \langle {\lambda _k}\right \rangle }$
be the sequence given by TSP(9).
${\left \langle {\lambda _k}\right \rangle }$
be the sequence given by TSP(9).
Suppose that
![]() $s(\sigma )=0$
. If
$s(\sigma )=0$
. If
![]() $\sigma \in W_0$
, then
$\sigma \in W_0$
, then
![]() $A_\sigma = \emptyset $
; if
$A_\sigma = \emptyset $
; if
![]() $\sigma \in W_1$
, then
$\sigma \in W_1$
, then
![]() ${A_\sigma = [\sigma ]^\prec _\lambda }$
. In either case, by TSP(9) and TSP(4),
${A_\sigma = [\sigma ]^\prec _\lambda }$
. In either case, by TSP(9) and TSP(4),
![]() $A_\sigma $
is
$A_\sigma $
is
![]() $\boldsymbol {\Sigma }^0_{1+\lambda _k}$
where
$\boldsymbol {\Sigma }^0_{1+\lambda _k}$
where
![]() $k = |\sigma |_\lambda $
, and so is in
$k = |\sigma |_\lambda $
, and so is in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Suppose that
![]() $s(\sigma )> 0$
, and thus
$s(\sigma )> 0$
, and thus
![]() $\sigma \in T$
. Let R be the collection of immediate
$\sigma \in T$
. Let R be the collection of immediate
![]() $\prec _\lambda $
-extensions of
$\prec _\lambda $
-extensions of
![]() $\sigma $
. By the inductive hypothesis,
$\sigma $
. By the inductive hypothesis,
![]() $A_\tau \in \mathcal {C}$
for every
$A_\tau \in \mathcal {C}$
for every
![]() $\tau \in R$
. Let
$\tau \in R$
. Let
![]() $k = |\sigma |_\lambda +1$
, so
$k = |\sigma |_\lambda +1$
, so
![]() $k = |\tau |_\lambda $
for all
$k = |\tau |_\lambda $
for all
![]() $\tau \in R$
. By TSP(9) (and TSP(4)), the sequence
$\tau \in R$
. By TSP(9) (and TSP(4)), the sequence
![]() $\langle {[\tau ]^\prec _\lambda }\rangle _{\tau \in R}$
shows that
$\langle {[\tau ]^\prec _\lambda }\rangle _{\tau \in R}$
shows that
![]() $\langle {A_\tau }\rangle _{\tau \in R}$
is
$\langle {A_\tau }\rangle _{\tau \in R}$
is
![]() $\boldsymbol {\Sigma }^0_{1+\lambda _k}$
-separated. Hence
$\boldsymbol {\Sigma }^0_{1+\lambda _k}$
-separated. Hence
![]() $A_\sigma = \bigcup _{\tau \in R} A_\tau $
is in
$A_\sigma = \bigcup _{\tau \in R} A_\tau $
is in
![]() $\mathcal {C}$
as well.
$\mathcal {C}$
as well.
Note that we did not actually need the sets
![]() $W_0$
and
$W_0$
and
![]() $W_1$
to be c.e. In other words, it was enough that A is
$W_1$
to be c.e. In other words, it was enough that A is
![]() $(z,\lambda )$
-clopen for some parameter z; we didn’t use the fact that it is effectively
$(z,\lambda )$
-clopen for some parameter z; we didn’t use the fact that it is effectively
![]() $(z,\lambda )$
-clopen, i.e.,
$(z,\lambda )$
-clopen, i.e.,
![]() $\Delta ^0_\lambda (z)$
. Nevertheless, the proof can be made entirely effective, and an effective version of Wadge’s theorem is true.
$\Delta ^0_\lambda (z)$
. Nevertheless, the proof can be made entirely effective, and an effective version of Wadge’s theorem is true.
To state it, for a lightface class
![]() $\Gamma $
and a computable ordinal
$\Gamma $
and a computable ordinal
![]() $\xi $
, let
$\xi $
, let
![]() $\text {SU}_{\xi }(\Gamma )$
be the collection of unions of all sequences of sets which are uniformly in
$\text {SU}_{\xi }(\Gamma )$
be the collection of unions of all sequences of sets which are uniformly in
![]() $\Gamma $
and uniformly
$\Gamma $
and uniformly
![]() $\Sigma ^0_\xi $
-separated. For a computable limit ordinal
$\Sigma ^0_\xi $
-separated. For a computable limit ordinal
![]() $\lambda $
define by induction on
$\lambda $
define by induction on
![]() $\beta <\omega _1^{\text {ck}}$
the lightface classes
$\beta <\omega _1^{\text {ck}}$
the lightface classes
![]() $\text {ISU}^{(\beta )}_{\lambda }$
(iterated separated unions):
$\text {ISU}^{(\beta )}_{\lambda }$
(iterated separated unions):
-
•
 $\text {ISU}^{(<0)}_{\lambda } = \Sigma ^0_{<\lambda } = \bigcup _{\xi <\lambda }\Sigma ^0_\xi $
.
$\text {ISU}^{(<0)}_{\lambda } = \Sigma ^0_{<\lambda } = \bigcup _{\xi <\lambda }\Sigma ^0_\xi $
. -
• For
 $\beta>0$
,
$\beta>0$
,
 $\text {ISU}^{(<\beta )}_{\lambda } = \bigcup _{\gamma <\beta } \text {ISU}^{(\gamma )}_{\lambda }$
.
$\text {ISU}^{(<\beta )}_{\lambda } = \bigcup _{\gamma <\beta } \text {ISU}^{(\gamma )}_{\lambda }$
. -
•
 $\text {ISU}^{(\beta )}_{\lambda } = \text {SU}_{<\lambda }(\text {ISU}^{(<\beta )}_{\lambda }) = \bigcup _{\xi <\lambda }\text {SU}_{\xi }(\text {ISU}^{(<\beta )}_{\lambda })$
.
$\text {ISU}^{(\beta )}_{\lambda } = \text {SU}_{<\lambda }(\text {ISU}^{(<\beta )}_{\lambda }) = \bigcup _{\xi <\lambda }\text {SU}_{\xi }(\text {ISU}^{(<\beta )}_{\lambda })$
.
Each class
![]() $\text {ISU}^{(\beta )}_{\lambda }$
depends on a choice of computable copy of
$\text {ISU}^{(\beta )}_{\lambda }$
depends on a choice of computable copy of
![]() $\beta $
; given such a copy, we can give an effective enumeration of the class
$\beta $
; given such a copy, we can give an effective enumeration of the class
![]() $\text {ISU}^{(<\beta )}_{\lambda }$
, so we can indeed speak of a sequence of sets being uniformly in this class. The effective version of Wadge’s theorem is:
$\text {ISU}^{(<\beta )}_{\lambda }$
, so we can indeed speak of a sequence of sets being uniformly in this class. The effective version of Wadge’s theorem is:
Theorem 3.13. Let
![]() $\lambda <\omega _1^{\text {ck}}$
be a limit ordinal. Then
$\lambda <\omega _1^{\text {ck}}$
be a limit ordinal. Then
The proof above effectivises; as in the proof of Theorem 3.3, we can make r a computable ranking function into a computable ordinal (by taking the Kleene–Brouwer ordering on T). Then, by effective transfinite recursion on T (from the leaves to the root), we show that
![]() $A_\sigma \in \text {ISU}^{(s(\sigma ))}_{\lambda }$
, uniformly so.
$A_\sigma \in \text {ISU}^{(s(\sigma ))}_{\lambda }$
, uniformly so.
4 Louveau and Saint Raymond’s separation theorem
We begin by recalling Louveau and Saint Raymond’s separation theorem.
Theorem 4.1 (Louveau and Saint Raymond [Reference Louveau and Saint Raymond36]).
Suppose that
![]() $A \in \boldsymbol {\Sigma }^0_{1+\xi }$
and that
$A \in \boldsymbol {\Sigma }^0_{1+\xi }$
and that
![]() $B_0$
and
$B_0$
and
![]() $B_1$
are disjoint
$B_1$
are disjoint
![]() $\boldsymbol {\Sigma }^1_1$
sets. Then at least one of the following holds:
$\boldsymbol {\Sigma }^1_1$
sets. Then at least one of the following holds:
-
• There is a continuous function f such that
 $A = f^{-1}(B_1)$
and
$A = f^{-1}(B_1)$
and
 ${A^\complement = f^{-1}(B_0)}$
.
${A^\complement = f^{-1}(B_0)}$
. -
• There is a
 $\mathbf {\Sigma }^0_{1+\xi }$
set U with
$\mathbf {\Sigma }^0_{1+\xi }$
set U with
 $B_0 \subseteq U$
and
$B_0 \subseteq U$
and
 $B_1 \cap U = \emptyset $
.
$B_1 \cap U = \emptyset $
.
In [Reference Louveau and Saint Raymond37], Louveau and Saint Raymond extend this theorem by considering all non-self-dual Borel Wadge class. Further, in that paper, the authors note that their proof is sufficiently effective to yield the following:
Theorem 4.2. Fix
![]() $\xi < \omega _1^{\text {ck}}$
. Suppose that
$\xi < \omega _1^{\text {ck}}$
. Suppose that
![]() $A \in \Sigma ^0_{1+\xi }$
and that
$A \in \Sigma ^0_{1+\xi }$
and that
![]() $B_0$
and
$B_0$
and
![]() $B_1$
are disjoint
$B_1$
are disjoint
![]() $\Sigma ^1_1$
sets. Then at least one of the following holds:
$\Sigma ^1_1$
sets. Then at least one of the following holds:
-
• There is a continuous function f such that
 $A = f^{-1}(B_1)$
and
$A = f^{-1}(B_1)$
and
 ${A^\complement = f^{-1}(B_0)}$
.
${A^\complement = f^{-1}(B_0)}$
. -
• There is a
 $\Sigma ^0_{1+\xi }(\Delta ^1_1)$
set U with
$\Sigma ^0_{1+\xi }(\Delta ^1_1)$
set U with
 $B_0 \subseteq U$
and
$B_0 \subseteq U$
and
 $B_1 \cap U = \emptyset $
.
$B_1 \cap U = \emptyset $
.
(Recall the notation
![]() $\Gamma (\Delta ^1_1)$
from Section 3.1.)
$\Gamma (\Delta ^1_1)$
from Section 3.1.)
As usual, Theorem 4.2 implies Theorem 4.1 by relativisation. By taking A to be a
![]() $\Sigma ^0_{1+\xi }$
-complete set (which is therefore not
$\Sigma ^0_{1+\xi }$
-complete set (which is therefore not
![]() $\boldsymbol {\Pi }^0_{1+\xi }$
), Theorem 4.2 implies Louveau’s celebrated separation theorem:
$\boldsymbol {\Pi }^0_{1+\xi }$
), Theorem 4.2 implies Louveau’s celebrated separation theorem:
Theorem 4.3 [Reference Louveau35].
Let
![]() $\xi <\omega _1^{\text {ck}}$
. If
$\xi <\omega _1^{\text {ck}}$
. If
![]() $B_0$
and
$B_0$
and
![]() $B_1$
are disjoint
$B_1$
are disjoint
![]() $\Sigma ^1_1$
sets and are separated by some
$\Sigma ^1_1$
sets and are separated by some
![]() $\boldsymbol {\Sigma }^0_{1+\xi }$
set, then they have a
$\boldsymbol {\Sigma }^0_{1+\xi }$
set, then they have a
![]() $\Sigma ^0_{1+\xi }(\Delta ^1_1)$
separator.
$\Sigma ^0_{1+\xi }(\Delta ^1_1)$
separator.
The proof of Theorem 4.2 in [Reference Louveau and Saint Raymond37] relies on a technique of unravelling complicated games into simpler ones. In [Reference Louveau and Saint Raymond36], before they introduce the technique, the authors present a simpler proof of Theorem 4.2 for
![]() $\xi = 1$
and
$\xi = 1$
and
![]() $\xi =2$
in which a closed game is directly defined without the need for unravelling. The proof we give is a generalisation of this simpler technique to all countable ordinals
$\xi =2$
in which a closed game is directly defined without the need for unravelling. The proof we give is a generalisation of this simpler technique to all countable ordinals
![]() $\xi $
. We remark that in [Reference Debs and Raymond10], Debs and Saint Raymond give another proof of Theorem 4.1, using their tree representations of Borel sets.
$\xi $
. We remark that in [Reference Debs and Raymond10], Debs and Saint Raymond give another proof of Theorem 4.1, using their tree representations of Borel sets.
Proof of Theorem 4.2
Fix computable trees
![]() $T_0$
,
$T_0$
,
![]() $T_1$
such that for
$T_1$
such that for
![]() $i=0,1$
,
$i=0,1$
,
![]() $B_i$
is the projection of
$B_i$
is the projection of
![]() $[T_i]$
:
$[T_i]$
:
![]() $B_i = \{ y \,:\, (\exists z)\,\, (y,z) \in [T_i]\}$
. By TSP(4), fix a computable, upwards-closed
$B_i = \{ y \,:\, (\exists z)\,\, (y,z) \in [T_i]\}$
. By TSP(4), fix a computable, upwards-closed
![]() $W\subseteq \omega ^{<\omega }$
such that
$W\subseteq \omega ^{<\omega }$
such that
![]() $[W]^\prec _\xi = A$
.
$[W]^\prec _\xi = A$
.
We define a two player game, in which players I and II alternate turns. On player I’s
![]() $i{}^{\text {th}}$
turn, they play
$i{}^{\text {th}}$
turn, they play
![]() $x_i \in \omega $
. On player II’s
$x_i \in \omega $
. On player II’s
![]() $i{}^{\text {th}}$
turn, they play
$i{}^{\text {th}}$
turn, they play
![]() $(y_i, z_i) \in \omega \times \omega $
. For our game, the set of runs in which player I wins will be an open set, so we will explain how to determine partway through the game if player I has already won.
$(y_i, z_i) \in \omega \times \omega $
. For our game, the set of runs in which player I wins will be an open set, so we will explain how to determine partway through the game if player I has already won.
Suppose that
![]() $n>0$
, player I has played
$n>0$
, player I has played
![]() $x_0, \dots , x_{n-1}$
, while player II has played
$x_0, \dots , x_{n-1}$
, while player II has played
![]() $(y_1, z_1)$
,
$(y_1, z_1)$
,
![]() $\dots $
,
$\dots $
,
![]() $(y_{n}, z_{n})$
(it is convenient to begin the indexing for player II at 1 rather than 0, so
$(y_{n}, z_{n})$
(it is convenient to begin the indexing for player II at 1 rather than 0, so
![]() $(y_n,z_n)$
is player II’s response after player I has played a sequence of length n). Before letting player I’s take another turn, we will determine if they have already won. Let
$(y_n,z_n)$
is player II’s response after player I has played a sequence of length n). Before letting player I’s take another turn, we will determine if they have already won. Let
![]() $\overline {x} = (x_0, \dots , x_{n-1}) \in \omega ^{<\omega }$
. Then
$\overline {x} = (x_0, \dots , x_{n-1}) \in \omega ^{<\omega }$
. Then
![]() $\overline {x}$
has an opinion as to whether the real x which player I is building will be in A: the opinion is determined by whether
$\overline {x}$
has an opinion as to whether the real x which player I is building will be in A: the opinion is determined by whether
![]() $\overline {x} \in W$
or not. Whichever it is, player II is responsible for building a real y in
$\overline {x} \in W$
or not. Whichever it is, player II is responsible for building a real y in
![]() $B_0$
or
$B_0$
or
![]() $B_1$
, as appropriate, and also a z which witnesses y’s membership. However, we will only ask player II to make progress on constructing z at those stages which appear
$B_1$
, as appropriate, and also a z which witnesses y’s membership. However, we will only ask player II to make progress on constructing z at those stages which appear
![]() $\xi $
-true at the current stage and which share this opinion about x. This is made precise in the following.
$\xi $
-true at the current stage and which share this opinion about x. This is made precise in the following.
Define a set of indices F as follows:
-
• If
 $\overline {x} \in W$
, let
$\overline {x} \in W$
, let
 $F = \{ i \in \{1,\dots , n\} : \overline {x}\! \upharpoonright \!{i} \preceq _\xi \overline {x} \,\,\,\&\,\,\, \overline {x}\! \upharpoonright \!{i} \in W\}$
.
$F = \{ i \in \{1,\dots , n\} : \overline {x}\! \upharpoonright \!{i} \preceq _\xi \overline {x} \,\,\,\&\,\,\, \overline {x}\! \upharpoonright \!{i} \in W\}$
. -
• If
 $\overline {x} \notin W$
, let
$\overline {x} \notin W$
, let
 $F = \{ i \in \{1,\dots , n\} : \overline {x}\! \upharpoonright \!{i} \preceq _\xi \overline {x} \}$
.
$F = \{ i \in \{1,\dots , n\} : \overline {x}\! \upharpoonright \!{i} \preceq _\xi \overline {x} \}$
.
Note that
![]() $n \in F$
. Also note that since W is upwards-closed in
$n \in F$
. Also note that since W is upwards-closed in
![]() $(\omega ^{<\omega }, \preceq _\xi )$
, if
$(\omega ^{<\omega }, \preceq _\xi )$
, if
![]() $\overline {x}\notin W$
then
$\overline {x}\notin W$
then
![]() $\overline {x}\! \upharpoonright \!{i}\notin W$
for all
$\overline {x}\! \upharpoonright \!{i}\notin W$
for all
![]() $i\in F$
.
$i\in F$
.
Enumerate F as
![]() $F = \{ a_0 < \dots < a_{k-1}\}$
, so
$F = \{ a_0 < \dots < a_{k-1}\}$
, so
![]() $k \geqslant 1$
. Let
$k \geqslant 1$
. Let
![]() $\overline {y} = (y_1, \dots , y_k)$
and
$\overline {y} = (y_1, \dots , y_k)$
and
![]() $\overline {z} = (z_{a_0}, \dots , z_{a_{k-1}})$
, observing the difference in the subscripts: for
$\overline {z} = (z_{a_0}, \dots , z_{a_{k-1}})$
, observing the difference in the subscripts: for
![]() $\overline {z}$
, we only collect the numbers played by player II in response to initial segments of
$\overline {z}$
, we only collect the numbers played by player II in response to initial segments of
![]() $\overline {x}$
which appear to be correct, whereas for
$\overline {x}$
which appear to be correct, whereas for
![]() $\overline {(y)}$
, we take the initial segment of length k of the
$\overline {(y)}$
, we take the initial segment of length k of the
![]() $y_i$
’s played so far.
$y_i$
’s played so far.
We declare that player I wins if:
-
•
 $\overline {x} \in W$
and
$\overline {x} \in W$
and
 $(\overline {y}, \overline {z}) \not \in T_1$
; or
$(\overline {y}, \overline {z}) \not \in T_1$
; or -
•
 $\overline {x} \not \in W$
and
$\overline {x} \not \in W$
and
 $(\overline {y}, \overline {z}) \not \in T_0$
.
$(\overline {y}, \overline {z}) \not \in T_0$
.
Otherwise, the game continues. If the game continues for
![]() $\omega $
many turns, then player II wins.
$\omega $
many turns, then player II wins.
As this is an open/closed game, it is determined.
Claim 4.2.1. If player II has a winning strategy in the game, then there is a continuous function reducing
![]() $(A^\complement ,A)$
to
$(A^\complement ,A)$
to
![]() $(B_0,B_1)$
.
$(B_0,B_1)$
.
Proof Suppose that S is a winning strategy for player II. For
![]() $x \in \mathcal {N}$
, let
$x \in \mathcal {N}$
, let
![]() $y, z \in \mathcal {N}$
be the sequences generated by player II when player I plays x and player II plays according to S. We claim that
$y, z \in \mathcal {N}$
be the sequences generated by player II when player I plays x and player II plays according to S. We claim that
![]() $x \mapsto y$
is our desired continuous reduction.
$x \mapsto y$
is our desired continuous reduction.
If
![]() $x \in A$
, let
$x \in A$
, let
![]() $a_0 < a_1 < \cdots $
enumerate those
$a_0 < a_1 < \cdots $
enumerate those
![]() $a < \omega $
with
$a < \omega $
with
![]() $x\! \upharpoonright \!{a} \preceq _\xi x$
and
$x\! \upharpoonright \!{a} \preceq _\xi x$
and
![]() $x\! \upharpoonright \!{a} \in W$
. Let
$x\! \upharpoonright \!{a} \in W$
. Let
![]() $v = (z_{a_0}, z_{a_1}, \dots )$
. Then for each k, since player II had not lost after round
$v = (z_{a_0}, z_{a_1}, \dots )$
. Then for each k, since player II had not lost after round
![]() $a_k{}^{\text {th}}$
of the game,
$a_k{}^{\text {th}}$
of the game,
![]() $(y\! \upharpoonright \!{k}, v\! \upharpoonright \!{k}) \in T_1$
. So
$(y\! \upharpoonright \!{k}, v\! \upharpoonright \!{k}) \in T_1$
. So
![]() $(y, v) \in [T_1]$
, and thus
$(y, v) \in [T_1]$
, and thus
![]() $y \in B_1$
as desired.
$y \in B_1$
as desired.
If
![]() $x \not \in A$
, let
$x \not \in A$
, let
![]() $a_0 < a_1 < \cdots $
enumerate those
$a_0 < a_1 < \cdots $
enumerate those
![]() $a < \omega $
with
$a < \omega $
with
![]() $x\! \upharpoonright \!{a} \preceq _\xi x$
; note that
$x\! \upharpoonright \!{a} \preceq _\xi x$
; note that
![]() $x\! \upharpoonright \!{a} \not \in W$
for such a. The same argument shows that
$x\! \upharpoonright \!{a} \not \in W$
for such a. The same argument shows that
![]() $y \in B_0$
, as desired.
$y \in B_0$
, as desired.
Now suppose instead that player I has a winning strategy S in the game. In the rest of the proof, we show how to use S to construct a
![]() $\Sigma ^0_{1+\xi }(S)$
separator between
$\Sigma ^0_{1+\xi }(S)$
separator between
![]() $B_0$
and
$B_0$
and
![]() $B_1$
. Since the game is open for player I, there is a hyperarithmetic winning strategy S, so the separator can be taken to be
$B_1$
. Since the game is open for player I, there is a hyperarithmetic winning strategy S, so the separator can be taken to be
![]() $\Sigma ^0_{1+\xi }(\Delta ^1_1)$
as required.
$\Sigma ^0_{1+\xi }(\Delta ^1_1)$
as required.
For
![]() $y \in \mathcal {N}$
and
$y \in \mathcal {N}$
and
![]() $\sigma \in \omega ^{<\omega }$
, let
$\sigma \in \omega ^{<\omega }$
, let
![]() $S(y, \sigma )$
be the sequence
$S(y, \sigma )$
be the sequence
![]() $(x_0, \dots , x_n)$
which results from player I playing according to S and player II playing
$(x_0, \dots , x_n)$
which results from player I playing according to S and player II playing
![]() $(y\! \upharpoonright \!{|\sigma |}, \sigma )$
. Note that
$(y\! \upharpoonright \!{|\sigma |}, \sigma )$
. Note that
![]() $|S(y,\sigma )|= |\sigma |+1$
. It will be notationally convenient to posit the existence of a string
$|S(y,\sigma )|= |\sigma |+1$
. It will be notationally convenient to posit the existence of a string
![]() $\pi $
with
$\pi $
with
![]() $|\pi | = -1$
and
$|\pi | = -1$
and
![]() $S(y, \pi ) = {\left \langle {}\right \rangle }$
.
$S(y, \pi ) = {\left \langle {}\right \rangle }$
.
Roughly, the idea is the following. Given y, we need to decide whether to put it into the separator U or not. We put it into U (the side that will contain
![]() $B_0$
) if there is some “credible”
$B_0$
) if there is some “credible”
![]() $\sigma $
for which
$\sigma $
for which
![]() $S(y,\sigma )\in W$
. We need to ensure that if there is such
$S(y,\sigma )\in W$
. We need to ensure that if there is such
![]() $\sigma $
then
$\sigma $
then
![]() $y\notin B_1$
(and similarly, if there is no such
$y\notin B_1$
(and similarly, if there is no such
![]() $\sigma $
, then
$\sigma $
, then
![]() $y\notin B_0$
). The argument for contradiction will be that if
$y\notin B_0$
). The argument for contradiction will be that if
![]() $y\in B_1$
, say
$y\in B_1$
, say
![]() $(y,z)\in [T_1]$
, then we can start from
$(y,z)\in [T_1]$
, then we can start from
![]() $\sigma $
and use z to defeat S. To do this, we will define a sequence
$\sigma $
and use z to defeat S. To do this, we will define a sequence
![]() $\sigma _0,\sigma _1,\dots $
such that for each i, after player I’s response to our play of
$\sigma _0,\sigma _1,\dots $
such that for each i, after player I’s response to our play of
![]() $(y,\sigma _i)$
, we can play
$(y,\sigma _i)$
, we can play
![]() $z_i$
and continue to the next
$z_i$
and continue to the next
![]() $\sigma _{i+1}$
. The notion of credibility of a sequence, which also allows us to continue the inductive construction, is that of a “strongly
$\sigma _{i+1}$
. The notion of credibility of a sequence, which also allows us to continue the inductive construction, is that of a “strongly
![]() $\xi $
-correct” sequence (Definition 4.2.3). The complexity of the separator depends on the complexity of this notion of correctness, which is computed in Claim 4.2.5. The heart of the argument is Claim 4.2.6, which ensures that we can take another step in the construction we outlined.
$\xi $
-correct” sequence (Definition 4.2.3). The complexity of the separator depends on the complexity of this notion of correctness, which is computed in Claim 4.2.5. The heart of the argument is Claim 4.2.6, which ensures that we can take another step in the construction we outlined.
We will use the strategy S to pull back the true stage relations onto strings
![]() $\sigma $
, which we think of as potential second coordinates for player II to play along a given real y.
$\sigma $
, which we think of as potential second coordinates for player II to play along a given real y.
Definition 4.2.2. Let
![]() $\alpha \leqslant \xi $
and
$\alpha \leqslant \xi $
and
![]() $y \in \mathcal {N}$
. For
$y \in \mathcal {N}$
. For
![]() $\sigma , \tau \in \omega ^{<\omega }\cup \{\pi \}$
, we write
$\sigma , \tau \in \omega ^{<\omega }\cup \{\pi \}$
, we write
![]() $\sigma \trianglelefteq _\alpha ^y \tau $
when
$\sigma \trianglelefteq _\alpha ^y \tau $
when
![]() $\sigma \preceq \tau $
and
$\sigma \preceq \tau $
and
![]() $S(y, \sigma ) \preceq _\alpha S(y, \tau )$
.
$S(y, \sigma ) \preceq _\alpha S(y, \tau )$
.
We will now define a sort of absolutely true stage for these new relations, moderated by the need to avoid letting player I win.
Definition 4.2.3. For
![]() $y \in \omega ^\omega $
,
$y \in \omega ^\omega $
,
![]() $\sigma \in \omega ^{<\omega } \cup \{\pi \}$
, and
$\sigma \in \omega ^{<\omega } \cup \{\pi \}$
, and
![]() $\alpha \leqslant \xi $
, we define what it means for
$\alpha \leqslant \xi $
, we define what it means for
![]() $\sigma $
to be
$\sigma $
to be
![]() $\alpha $
-correct or strongly
$\alpha $
-correct or strongly
![]() $\alpha $
-correct for y.
$\alpha $
-correct for y.
-
•
 $\sigma $
is 0-correct for y if in the partial play of the game where player II plays
$\sigma $
is 0-correct for y if in the partial play of the game where player II plays
 $(y\! \upharpoonright \!{|\sigma |}, \sigma )$
and player I plays according to S, player I has not yet won.
$(y\! \upharpoonright \!{|\sigma |}, \sigma )$
and player I plays according to S, player I has not yet won. -
•
 $\sigma $
is
$\sigma $
is
 $(\alpha +1)$
-correct for y if it is strongly
$(\alpha +1)$
-correct for y if it is strongly
 $\alpha $
-correct for y, and for every
$\alpha $
-correct for y, and for every
 $\tau \trianglerighteq ^{y}_{\alpha } \sigma $
which is strongly
$\tau \trianglerighteq ^{y}_{\alpha } \sigma $
which is strongly
 $\alpha $
-correct for y,
$\alpha $
-correct for y,
 $\tau \trianglerighteq ^{y}_{\alpha +1} \sigma $
.
$\tau \trianglerighteq ^{y}_{\alpha +1} \sigma $
. -
• For
 $\lambda $
a limit,
$\lambda $
a limit,
 $\sigma $
is
$\sigma $
is
 $\lambda $
-correct for y if it is
$\lambda $
-correct for y if it is
 $\beta $
-correct for y for all
$\beta $
-correct for y for all
 $\beta < \lambda $
.
$\beta < \lambda $
. -
•
 $\sigma $
is strongly
$\sigma $
is strongly
 $\alpha $
-correct for y if for every
$\alpha $
-correct for y if for every
 $\tau \trianglelefteq _\alpha ^y \sigma $
,
$\tau \trianglelefteq _\alpha ^y \sigma $
,
 $\tau $
is
$\tau $
is
 $\alpha $
-correct for y.
$\alpha $
-correct for y.
Claim 4.2.4. Let
![]() $y\in \mathcal {N}$
,
$y\in \mathcal {N}$
,
![]() $\alpha \leqslant \xi $
, and
$\alpha \leqslant \xi $
, and
![]() $\sigma \in \omega ^{<\omega }\cup \{\pi \}$
.
$\sigma \in \omega ^{<\omega }\cup \{\pi \}$
.
-
(a) If
 $\sigma $
is strongly
$\sigma $
is strongly
 $\alpha $
-correct for y, then it is
$\alpha $
-correct for y, then it is
 $\alpha $
-correct for y.
$\alpha $
-correct for y. -
(b)
 $\sigma $
is strongly 0-correct for y if and only if it is 0-correct for y.
$\sigma $
is strongly 0-correct for y if and only if it is 0-correct for y. -
(c) If
 $\sigma $
is
$\sigma $
is
 $\alpha $
-correct for y, then it is strongly
$\alpha $
-correct for y, then it is strongly
 $\beta $
-correct for y for every
$\beta $
-correct for y for every
 $\beta < \alpha $
.
$\beta < \alpha $
. -
(d) If
 $\sigma $
is strongly
$\sigma $
is strongly
 $\alpha $
-correct for y, then every
$\alpha $
-correct for y, then every
 $\rho \trianglelefteq _\alpha ^y \sigma $
is strongly
$\rho \trianglelefteq _\alpha ^y \sigma $
is strongly
 $\alpha $
-correct for y.
$\alpha $
-correct for y. -
(e) If
 $\sigma \preceq \tau $
and both
$\sigma \preceq \tau $
and both
 $\sigma $
and
$\sigma $
and
 $\tau $
are
$\tau $
are
 $\alpha $
-correct for y, then
$\alpha $
-correct for y, then
 $\sigma \trianglelefteq ^y_\alpha \tau $
.
$\sigma \trianglelefteq ^y_\alpha \tau $
. -
(f)
 $\pi $
is strongly
$\pi $
is strongly
 $\alpha $
-correct for y.
$\alpha $
-correct for y.
Proof (a) follows from the relations
![]() $\preceq _\alpha $
(and thus
$\preceq _\alpha $
(and thus
![]() $\trianglelefteq ^y_\alpha $
) being reflexive. (b) holds because once player I wins, the game ends. (c) is by induction on
$\trianglelefteq ^y_\alpha $
) being reflexive. (b) holds because once player I wins, the game ends. (c) is by induction on
![]() $\alpha $
. (d) follows from the transitivity of
$\alpha $
. (d) follows from the transitivity of
![]() $\preceq _\alpha $
(and thus of
$\preceq _\alpha $
(and thus of
![]() $\trianglelefteq _\alpha ^y$
). (e) is proved by induction on
$\trianglelefteq _\alpha ^y$
). (e) is proved by induction on
![]() $\alpha $
. (f) follows from
$\alpha $
. (f) follows from
![]() ${\left \langle {}\right \rangle }\preceq _\alpha \sigma $
for all
${\left \langle {}\right \rangle }\preceq _\alpha \sigma $
for all
![]() $\sigma $
(TSP(2)).
$\sigma $
(TSP(2)).
Note that (d) and (e) of Claim 4.2.4 together imply that if
![]() $\sigma $
is strongly
$\sigma $
is strongly
![]() $\alpha $
-correct for y, then for all
$\alpha $
-correct for y, then for all
![]() $\rho \preceq \sigma $
,
$\rho \preceq \sigma $
,
![]() $\rho \trianglelefteq _\alpha ^y \sigma $
if and only if
$\rho \trianglelefteq _\alpha ^y \sigma $
if and only if
![]() $\rho $
is strongly
$\rho $
is strongly
![]() $\alpha $
-correct for y if and only if
$\alpha $
-correct for y if and only if
![]() $\rho $
is
$\rho $
is
![]() $\alpha $
-correct for y.
$\alpha $
-correct for y.
Claim 4.2.5. Let
![]() $\alpha \leqslant \xi $
. The relations “
$\alpha \leqslant \xi $
. The relations “
![]() $\sigma $
is
$\sigma $
is
![]() $\alpha $
-correct for y” and “
$\alpha $
-correct for y” and “
![]() $\sigma $
is strongly
$\sigma $
is strongly
![]() $\alpha $
-correct for y” are:
$\alpha $
-correct for y” are:
-
(i)
 $\Delta ^0_1(S)$
if
$\Delta ^0_1(S)$
if
 $\alpha =0$
;
$\alpha =0$
; -
(ii)
 $\Pi ^0_\alpha (S)$
if
$\Pi ^0_\alpha (S)$
if
 $0<\alpha <\omega $
;
$0<\alpha <\omega $
; -
(iii)
 $\Delta ^0_\alpha (S)$
for limit
$\Delta ^0_\alpha (S)$
for limit
 $\alpha $
; and
$\alpha $
; and -
(iv)
 $\Pi ^0_{\alpha -1}(S)$
if
$\Pi ^0_{\alpha -1}(S)$
if
 $\alpha>\omega $
is a successor.
$\alpha>\omega $
is a successor.
Proof We prove this by induction on
![]() $\alpha $
. Technically, of course, this is an instance of effective transfinite recursion: for the limit case, we need the relations to be uniformly in their classes. For every
$\alpha $
. Technically, of course, this is an instance of effective transfinite recursion: for the limit case, we need the relations to be uniformly in their classes. For every
![]() $\alpha $
, the complexity of the strong relation follows from the complexity of “
$\alpha $
, the complexity of the strong relation follows from the complexity of “
![]() $\sigma $
is
$\sigma $
is
![]() $\alpha $
-correct for y” by the fact that the relations
$\alpha $
-correct for y” by the fact that the relations
![]() $\leqslant _\alpha $
are uniformly computable (TSP(8)).
$\leqslant _\alpha $
are uniformly computable (TSP(8)).
All cases are immediate, except for the limit case (iii). Suppose that
![]() $\lambda \leqslant \xi $
is a limit ordinal. We use TSP(9); let
$\lambda \leqslant \xi $
is a limit ordinal. We use TSP(9); let
![]() ${\left \langle {\lambda _k}\right \rangle }$
be given by that property.
${\left \langle {\lambda _k}\right \rangle }$
be given by that property.
Given y and
![]() $\sigma $
, let
$\sigma $
, let
![]() $k = |S(y,\sigma )|_\lambda $
. We claim that
$k = |S(y,\sigma )|_\lambda $
. We claim that
![]() $\sigma $
is
$\sigma $
is
![]() $\lambda $
-correct for y if and only if it is strongly
$\lambda $
-correct for y if and only if it is strongly
![]() $\lambda _k$
-correct for y. One direction follows from Claim 4.2.4(c). For the other direction, suppose that
$\lambda _k$
-correct for y. One direction follows from Claim 4.2.4(c). For the other direction, suppose that
![]() $\sigma $
is strongly
$\sigma $
is strongly
![]() $\lambda _k$
-correct for y. By induction on
$\lambda _k$
-correct for y. By induction on
![]() $\beta \in [\lambda _k,\lambda ]$
, we can show that every
$\beta \in [\lambda _k,\lambda ]$
, we can show that every
![]() $\rho \trianglelefteq ^y_{\lambda _k} \sigma $
is strongly
$\rho \trianglelefteq ^y_{\lambda _k} \sigma $
is strongly
![]() $\beta $
-correct for y.
$\beta $
-correct for y.
This is mostly chasing the definitions, using Claim 4.2.4. The main point is that for all
![]() $\rho \trianglelefteq ^y_{\lambda _k} \sigma $
we have
$\rho \trianglelefteq ^y_{\lambda _k} \sigma $
we have
![]() $|S(y,\rho )|_{\lambda _k} = |S(y,\rho )|_\lambda \leqslant k$
, and so for all
$|S(y,\rho )|_{\lambda _k} = |S(y,\rho )|_\lambda \leqslant k$
, and so for all
![]() $\tau $
, if
$\tau $
, if
![]() $\rho \trianglelefteq ^y_{\beta } \tau $
then
$\rho \trianglelefteq ^y_{\beta } \tau $
then
![]() $\rho \trianglelefteq ^y_\lambda \tau $
, and so
$\rho \trianglelefteq ^y_\lambda \tau $
, and so
![]() $\rho \trianglelefteq ^y_{\beta +1} \tau $
.
$\rho \trianglelefteq ^y_{\beta +1} \tau $
.
The following is the main part of the proof.
Claim 4.2.6. Let
![]() $y \in \mathcal {N}$
and
$y \in \mathcal {N}$
and
![]() $\alpha \leqslant \xi $
. Suppose that
$\alpha \leqslant \xi $
. Suppose that
![]() $\rho \in \omega ^{<\omega }\cup \{\pi \}$
is strongly
$\rho \in \omega ^{<\omega }\cup \{\pi \}$
is strongly
![]() $\alpha $
-correct for y. If
$\alpha $
-correct for y. If
![]() $\sigma $
is a one-element extension of
$\sigma $
is a one-element extension of
![]() $\rho $
which is 0-correct for y, then there exists a
$\rho $
which is 0-correct for y, then there exists a
![]() $\tau \succeq \sigma $
which is strongly
$\tau \succeq \sigma $
which is strongly
![]() $\alpha $
-correct for y.
$\alpha $
-correct for y.
For the purposes of this claim, the empty sequence is a one-element extension of
![]() $\pi $
.
$\pi $
.
The idea of the proof of Claim 4.2.6 can be buried by its technical details. To explain it better, it would be useful to show how the claim is used. We therefore give the rest of the proof of Theorem 4.2 first.
We define a separator:
By Claim 4.2.5, the set U is
![]() $\Sigma ^0_{1+\xi }(S)$
. We need to show that
$\Sigma ^0_{1+\xi }(S)$
. We need to show that
![]() $B_0\subseteq U$
and
$B_0\subseteq U$
and
![]() $B_1\subseteq U^\complement $
.
$B_1\subseteq U^\complement $
.
Suppose, for a contradiction, that there is some
![]() $y\in U\cap B_1$
. Fix
$y\in U\cap B_1$
. Fix
![]() ${v = (v_0, v_1, \dots ) \in \mathcal {N}}$
such that
${v = (v_0, v_1, \dots ) \in \mathcal {N}}$
such that
![]() $(y, v) \in [T_1]$
. We define a sequence
$(y, v) \in [T_1]$
. We define a sequence
![]() $\sigma _0\prec \sigma _1 \prec \cdots $
of sequences which together with y will give a play for II that defeats the strategy S. We ensure that:
$\sigma _0\prec \sigma _1 \prec \cdots $
of sequences which together with y will give a play for II that defeats the strategy S. We ensure that:
-
(i) each
 $\sigma _i$
is strongly
$\sigma _i$
is strongly
 $\xi $
-correct for y;
$\xi $
-correct for y; -
(ii)
 $\sigma _{i+1}(|\sigma _i|) = v_i$
; and
$\sigma _{i+1}(|\sigma _i|) = v_i$
; and -
(iii) for each i,
 $$\begin{align*}\{\rho \in \omega^{<\omega} \,:\, \rho \trianglelefteq^y_\xi \sigma_i \,\,\,\&\,\,\, S(y, \rho) \in W\} = \{ \sigma_j \,:\, j \leqslant i\}. \end{align*}$$
$$\begin{align*}\{\rho \in \omega^{<\omega} \,:\, \rho \trianglelefteq^y_\xi \sigma_i \,\,\,\&\,\,\, S(y, \rho) \in W\} = \{ \sigma_j \,:\, j \leqslant i\}. \end{align*}$$
For
![]() $\sigma _0$
, we choose some sequence witnessing that
$\sigma _0$
, we choose some sequence witnessing that
![]() $y\in U$
, minimal such; so for all
$y\in U$
, minimal such; so for all
![]() $\rho \triangleleft ^y_\xi \sigma _0$
in
$\rho \triangleleft ^y_\xi \sigma _0$
in
![]() $\omega ^{<\omega }$
we have
$\omega ^{<\omega }$
we have
![]() $S(y,\rho )\notin W$
. Note that
$S(y,\rho )\notin W$
. Note that
![]() $\sigma _0\ne \pi $
. Suppose that
$\sigma _0\ne \pi $
. Suppose that
![]() $\sigma _i$
has been chosen. We then consider
$\sigma _i$
has been chosen. We then consider
![]() $\tau = \sigma _i\hat {\,\,} v_i$
; we wish to show that
$\tau = \sigma _i\hat {\,\,} v_i$
; we wish to show that
![]() $\tau $
is 0-correct for y, i.e., that player I does not win in response to
$\tau $
is 0-correct for y, i.e., that player I does not win in response to
![]() $(y\! \upharpoonright \!{|\tau |},\tau )$
. Since
$(y\! \upharpoonright \!{|\tau |},\tau )$
. Since
![]() $\sigma _i$
is
$\sigma _i$
is
![]() $\xi $
-correct for y, it is 0-correct for y; player I has not won after we play
$\xi $
-correct for y, it is 0-correct for y; player I has not won after we play
![]() $(y\! \upharpoonright \!{|\sigma _i|},\sigma _i)$
. After playing
$(y\! \upharpoonright \!{|\sigma _i|},\sigma _i)$
. After playing
![]() $(y\! \upharpoonright \!{|\tau |},\tau )$
, by (iii) above, the set F of indices used to assess whether I wins is
$(y\! \upharpoonright \!{|\tau |},\tau )$
, by (iii) above, the set F of indices used to assess whether I wins is
![]() $\{|\sigma _j|+1\,:\, j \leqslant i\}$
and so the corresponding
$\{|\sigma _j|+1\,:\, j \leqslant i\}$
and so the corresponding
![]() $\overline {z}$
is
$\overline {z}$
is
![]() $v\! \upharpoonright \!{(i+1)}$
. Since
$v\! \upharpoonright \!{(i+1)}$
. Since
![]() $(y\! \upharpoonright \!{(i+1)},\overline {z})\in T_1$
,
$(y\! \upharpoonright \!{(i+1)},\overline {z})\in T_1$
,
![]() $\tau $
is 0-correct for y as required.
$\tau $
is 0-correct for y as required.
We can therefore appeal to Claim 4.2.6. We choose
![]() $\sigma _{i+1}$
as given by the claim, of minimal length. This ensures (iii) for
$\sigma _{i+1}$
as given by the claim, of minimal length. This ensures (iii) for
![]() $i+1$
(we use the fact that W is upwards-closed in
$i+1$
(we use the fact that W is upwards-closed in
![]() $(\omega ^{<\omega },\preceq _\xi )$
).
$(\omega ^{<\omega },\preceq _\xi )$
).
The other case, that
![]() $y\in B_0\setminus U$
, is almost identical. In this case we will have
$y\in B_0\setminus U$
, is almost identical. In this case we will have
The empty sequence is 0-correct for y, and so by Claim 4.2.6 and Claim 4.2.4(f), there is some
![]() $\sigma \in \omega ^{<\omega }$
which is strongly
$\sigma \in \omega ^{<\omega }$
which is strongly
![]() $\xi $
-correct for y. We start with
$\xi $
-correct for y. We start with
![]() $\sigma _0$
being such a string of minimal length (by its choice,
$\sigma _0$
being such a string of minimal length (by its choice,
![]() $\sigma _0\ne \pi $
).
$\sigma _0\ne \pi $
).
This completes the proof of Theorem 4.2, given Claim 4.2.6. Toward the proof of Claim 4.2.6, let us use the construction just given to motivate the definitions of “
![]() $\alpha $
-correct” and “strongly
$\alpha $
-correct” and “strongly
![]() $\alpha $
-correct,” and explain the main part of the proof, which is the successor step.
$\alpha $
-correct,” and explain the main part of the proof, which is the successor step.
First, we explain why we need the strong version of correctness. Suppose that
![]() $\sigma _i$
is defined, and we are searching for a suitable
$\sigma _i$
is defined, and we are searching for a suitable
![]() $\sigma _{i+1}$
. If we take
$\sigma _{i+1}$
. If we take
![]() $\sigma _{i+1}$
to just be a minimal
$\sigma _{i+1}$
to just be a minimal
![]() $\xi $
-correct extension, we could accidentally have some
$\xi $
-correct extension, we could accidentally have some
![]() $\nu $
strictly between
$\nu $
strictly between
![]() $\sigma _i$
and
$\sigma _i$
and
![]() $\sigma _{i+1}$
with
$\sigma _{i+1}$
with
![]() $\sigma _i\trianglelefteq ^y_{\xi }\nu \trianglelefteq ^y_\xi \sigma _{i+1}$
. Then in computing whether player I won after playing
$\sigma _i\trianglelefteq ^y_{\xi }\nu \trianglelefteq ^y_\xi \sigma _{i+1}$
. Then in computing whether player I won after playing
![]() $\sigma _{i+1}$
, the response that
$\sigma _{i+1}$
, the response that
![]() $\sigma _{i+1}$
gives at round
$\sigma _{i+1}$
gives at round
![]() $|\nu |$
must be taken in consideration—but we have no control over it, in particular, cannot ensure that it is the appropriate bit of v.
$|\nu |$
must be taken in consideration—but we have no control over it, in particular, cannot ensure that it is the appropriate bit of v.
Next, for the definition of
![]() $\alpha $
-correctness. Consider the case
$\alpha $
-correctness. Consider the case
![]() $\xi =1$
. We are given
$\xi =1$
. We are given
![]() $\rho = \sigma _i$
and
$\rho = \sigma _i$
and
![]() $\sigma = \sigma _i\hat {\,\,} v_i$
, which is 0-correct for y, and so strongly 0-correct for y (Claim 4.2.4(b)). We need to find some
$\sigma = \sigma _i\hat {\,\,} v_i$
, which is 0-correct for y, and so strongly 0-correct for y (Claim 4.2.4(b)). We need to find some
![]() $\tau \succeq \sigma $
to be
$\tau \succeq \sigma $
to be
![]() $\sigma _{i+1}$
. First of all, we need
$\sigma _{i+1}$
. First of all, we need
![]() $\tau $
to not have already lost—it needs to be 0-correct. Next, we need
$\tau $
to not have already lost—it needs to be 0-correct. Next, we need
![]() $S(y,\rho )\preceq _1 S(y, \tau )$
, i.e.,
$S(y,\rho )\preceq _1 S(y, \tau )$
, i.e.,
![]() $\rho \trianglelefteq ^y_1 \tau $
. The definition of 1-correct ensures that in fact, any 0-correct extension of
$\rho \trianglelefteq ^y_1 \tau $
. The definition of 1-correct ensures that in fact, any 0-correct extension of
![]() $\rho $
satisfies this requirement. But then we need the construction to keep going, so we need to choose a strongly 1-correct extension.
$\rho $
satisfies this requirement. But then we need the construction to keep going, so we need to choose a strongly 1-correct extension.
How do we do that? Recall the function
![]() $p_\alpha $
given by TSP(7) (for
$p_\alpha $
given by TSP(7) (for
![]() $\alpha =1$
this is, roughly, the function telling us the last element enumerated into the jump set). Now among all (strongly) 0-correct extensions of
$\alpha =1$
this is, roughly, the function telling us the last element enumerated into the jump set). Now among all (strongly) 0-correct extensions of
![]() $\sigma $
, we choose one with
$\sigma $
, we choose one with
![]() $p_1(S(y,\tau ))$
minimal. Such
$p_1(S(y,\tau ))$
minimal. Such
![]() $\tau $
must be 1-correct: suppose that
$\tau $
must be 1-correct: suppose that
![]() $\eta $
is some 0-correct extension of
$\eta $
is some 0-correct extension of
![]() $\tau $
; we need
$\tau $
; we need
![]() $S(y,\tau )\preceq _1 S(y,\eta )$
. The string
$S(y,\tau )\preceq _1 S(y,\eta )$
. The string
![]() $\eta $
was one of the extensions of
$\eta $
was one of the extensions of
![]() $\sigma $
that was considered when choosing
$\sigma $
that was considered when choosing
![]() $\tau $
, so
$\tau $
, so
![]() $p_1(S(y,\tau ))\leqslant p_1(S(y,\eta ))$
, and in fact, this is true for all
$p_1(S(y,\tau ))\leqslant p_1(S(y,\eta ))$
, and in fact, this is true for all
![]() $\eta '$
with
$\eta '$
with
![]() $\tau \preceq \eta '\preceq \eta $
, as they are all 0-correct. So no such
$\tau \preceq \eta '\preceq \eta $
, as they are all 0-correct. So no such
![]() $\eta '$
could have seen that
$\eta '$
could have seen that
![]() $S(y,\tau )$
was wrong about the commitment it made about its jump, so we indeed get
$S(y,\tau )$
was wrong about the commitment it made about its jump, so we indeed get
![]() $S(y,\tau )\preceq _1 S(y,\eta )$
as required; technically, this informal argument about the jump is what stands behind TSP(7), and the desired conclusion is given by that property.
$S(y,\tau )\preceq _1 S(y,\eta )$
as required; technically, this informal argument about the jump is what stands behind TSP(7), and the desired conclusion is given by that property.
For the proof below, for
![]() $\alpha +1> 1$
, we need to first restrict the argument to strongly
$\alpha +1> 1$
, we need to first restrict the argument to strongly
![]() $\alpha $
-correct strings
$\alpha $
-correct strings
![]() $\eta $
, but we also need to show that the chosen
$\eta $
, but we also need to show that the chosen
![]() $\tau $
is strongly
$\tau $
is strongly
![]() $(\alpha +1)$
-correct, so we need to consider
$(\alpha +1)$
-correct, so we need to consider
![]() $\nu \trianglelefteq ^y_{\alpha +1} \tau $
; the details get a bit messy, but the main idea is the same.
$\nu \trianglelefteq ^y_{\alpha +1} \tau $
; the details get a bit messy, but the main idea is the same.
Proof of Claim 4.2.6
The argument is by induction on
![]() $\alpha $
. For
$\alpha $
. For
![]() $\alpha =0$
we can take
$\alpha =0$
we can take
![]() $\tau =\sigma $
(Claim 4.2.4(b)).
$\tau =\sigma $
(Claim 4.2.4(b)).
For the successor case, we use TSP(7). Suppose that the lemma holds for
![]() $\alpha <\xi $
, and suppose that
$\alpha <\xi $
, and suppose that
![]() $\rho $
is strongly
$\rho $
is strongly
![]() $(\alpha +1)$
-correct for y. Let
$(\alpha +1)$
-correct for y. Let
![]() $p_\alpha $
be given by TSP(7). For brevity, we will write
$p_\alpha $
be given by TSP(7). For brevity, we will write
![]() $p(\eta )$
in place of
$p(\eta )$
in place of
![]() $p_\alpha (S(y,\eta ))$
. By induction, there are
$p_\alpha (S(y,\eta ))$
. By induction, there are
![]() $\tau \succeq \sigma $
which are strongly
$\tau \succeq \sigma $
which are strongly
![]() $\alpha $
-correct for y. Amongst those
$\alpha $
-correct for y. Amongst those
![]() $\tau $
, choose one to minimize
$\tau $
, choose one to minimize
![]() $p(\tau )$
. We claim that this
$p(\tau )$
. We claim that this
![]() $\tau $
is strongly
$\tau $
is strongly
![]() $(\alpha +1)$
-correct for y. Note that since
$(\alpha +1)$
-correct for y. Note that since
![]() $\rho $
is
$\rho $
is
![]() $(\alpha +1)$
-correct for y and
$(\alpha +1)$
-correct for y and
![]() $\tau $
is strongly
$\tau $
is strongly
![]() $\alpha $
-correct for y,
$\alpha $
-correct for y,
![]() $\rho \trianglelefteq ^y_\alpha \tau $
(by Claim 4.2.4(e)) and so
$\rho \trianglelefteq ^y_\alpha \tau $
(by Claim 4.2.4(e)) and so
![]() $\rho \trianglelefteq _{\alpha +1}^y \tau $
(by Definition 4.2.3).
$\rho \trianglelefteq _{\alpha +1}^y \tau $
(by Definition 4.2.3).
We must show that every
![]() $\nu \trianglelefteq _{\alpha +1}^y \tau $
is
$\nu \trianglelefteq _{\alpha +1}^y \tau $
is
![]() $(\alpha +1)$
-correct for y. If
$(\alpha +1)$
-correct for y. If
![]() $\nu \prec \sigma $
, then
$\nu \prec \sigma $
, then
![]() $\nu \preceq \rho $
; since
$\nu \preceq \rho $
; since
![]() $\preceq _{\alpha +1}$
is a tree (TSP(2)),
$\preceq _{\alpha +1}$
is a tree (TSP(2)),
![]() $\nu \trianglelefteq _{\alpha +1}^y \rho $
. As
$\nu \trianglelefteq _{\alpha +1}^y \rho $
. As
![]() $\rho $
is strongly
$\rho $
is strongly
![]() $(\alpha +1)$
-correct for y,
$(\alpha +1)$
-correct for y,
![]() $\nu $
is
$\nu $
is
![]() $(\alpha +1)$
-correct for y. So we may assume that
$(\alpha +1)$
-correct for y. So we may assume that
![]() $\sigma \preceq \nu $
.
$\sigma \preceq \nu $
.
We need to show that for every
![]() $\eta \trianglerighteq ^{y}_{\alpha } \nu $
which is strongly
$\eta \trianglerighteq ^{y}_{\alpha } \nu $
which is strongly
![]() $\alpha $
-correct for y, it is the case that
$\alpha $
-correct for y, it is the case that
![]() $\nu \trianglelefteq _{\alpha +1}^y \eta $
. By TSP(7), since
$\nu \trianglelefteq _{\alpha +1}^y \eta $
. By TSP(7), since
![]() $\nu \trianglelefteq ^{y}_{\alpha +1} \tau $
,
$\nu \trianglelefteq ^{y}_{\alpha +1} \tau $
,
![]() $p(\nu ) \leqslant p(\tau )$
. As
$p(\nu ) \leqslant p(\tau )$
. As
![]() $\eta $
is strongly
$\eta $
is strongly
![]() $\alpha $
-correct for y, for every
$\alpha $
-correct for y, for every
![]() $\eta '$
with
$\eta '$
with
![]() $\nu \trianglelefteq _\alpha ^y \eta ' \trianglelefteq _\alpha ^y \eta $
,
$\nu \trianglelefteq _\alpha ^y \eta ' \trianglelefteq _\alpha ^y \eta $
,
![]() $\eta '$
is strongly
$\eta '$
is strongly
![]() $\alpha $
-correct for y (Claim 4.2.4(d)). Thus such
$\alpha $
-correct for y (Claim 4.2.4(d)). Thus such
![]() $\eta '$
was a candidate for
$\eta '$
was a candidate for
![]() $\tau $
, so
$\tau $
, so
![]() $p(\tau ) \leqslant p(\eta ')$
, and thus
$p(\tau ) \leqslant p(\eta ')$
, and thus
![]() $p(\nu ) \leqslant p(\eta ')$
. By TSP(7) again,
$p(\nu ) \leqslant p(\eta ')$
. By TSP(7) again,
![]() $\nu \trianglelefteq _{\alpha +1}^y \eta $
.
$\nu \trianglelefteq _{\alpha +1}^y \eta $
.
For
![]() $\alpha $
a limit, we again use TSP(9). Let
$\alpha $
a limit, we again use TSP(9). Let
![]() ${\left \langle {\alpha _k}\right \rangle }$
be a cofinal sequence in
${\left \langle {\alpha _k}\right \rangle }$
be a cofinal sequence in
![]() $\alpha $
supplied by that property; let
$\alpha $
supplied by that property; let
![]() $k = |S(y,\rho )|_\alpha +1$
. By induction, there is some
$k = |S(y,\rho )|_\alpha +1$
. By induction, there is some
![]() $\tau \succeq \sigma $
which is strongly
$\tau \succeq \sigma $
which is strongly
![]() $\alpha _k$
-correct for y. Among such
$\alpha _k$
-correct for y. Among such
![]() $\tau $
, fix one minimal with respect to
$\tau $
, fix one minimal with respect to
![]() $\trianglelefteq ^y_{\alpha _k}$
. So
$\trianglelefteq ^y_{\alpha _k}$
. So
![]() $\nu \triangleleft ^y_{\alpha _k} \tau $
implies
$\nu \triangleleft ^y_{\alpha _k} \tau $
implies
![]() $\nu \trianglelefteq ^y_{\alpha _k} \rho $
. Since
$\nu \trianglelefteq ^y_{\alpha _k} \rho $
. Since
![]() $|S(y,\nu )|_{\alpha _k} = |S(y,\nu )|_\alpha $
for all
$|S(y,\nu )|_{\alpha _k} = |S(y,\nu )|_\alpha $
for all
![]() $\nu \trianglelefteq ^y_{\alpha _k} \rho $
, we conclude that
$\nu \trianglelefteq ^y_{\alpha _k} \rho $
, we conclude that
![]() $|S(y,\tau )|_\alpha = k$
. Hence, for all
$|S(y,\tau )|_\alpha = k$
. Hence, for all
![]() $\eta $
, if
$\eta $
, if
![]() $\tau \trianglelefteq ^y_{\alpha _k} \eta $
then
$\tau \trianglelefteq ^y_{\alpha _k} \eta $
then
![]() $\tau \trianglelefteq ^y_\alpha \eta $
. As
$\tau \trianglelefteq ^y_\alpha \eta $
. As
![]() $\rho $
is strongly
$\rho $
is strongly
![]() $\alpha $
-correct for y, this suffices to show, by induction, on
$\alpha $
-correct for y, this suffices to show, by induction, on
![]() $\beta \in [\alpha _k,\alpha ]$
, that
$\beta \in [\alpha _k,\alpha ]$
, that
![]() $\tau $
is strongly
$\tau $
is strongly
![]() $\beta $
-correct for y.
$\beta $
-correct for y.
This completes the proof of Theorem 4.2.
As mentioned, Theorem 4.2 holds not just for the classes
![]() $\Sigma ^0_{1+\xi }$
, but for any non-self-dual Borel Wadge class, and our methods can be used to show this. From that, as in [Reference Louveau and Saint Raymond37], we can obtain Louveau separation for all non-self-dual Borel Wadge classes. The requirement
$\Sigma ^0_{1+\xi }$
, but for any non-self-dual Borel Wadge class, and our methods can be used to show this. From that, as in [Reference Louveau and Saint Raymond37], we can obtain Louveau separation for all non-self-dual Borel Wadge classes. The requirement
![]() $\xi < \omega _1^{\text {ck}}$
is replaced by the requirement that the Wadge class must have a
$\xi < \omega _1^{\text {ck}}$
is replaced by the requirement that the Wadge class must have a
![]() $\Delta ^1_1$
name. Of course, some care must be taken in defining what a name for a Wadge class is, and what the corresponding lightface class is. See the companion paper [Reference Day, Greenberg, Harrison-Trainor and Turetsky8] for further details. We further remark that the new system of descriptions of Borel Wadge classes is further explored in [Reference Greenberg and Turetsky17], where the authors give a new characterisation of the reduction property for these classes.
$\Delta ^1_1$
name. Of course, some care must be taken in defining what a name for a Wadge class is, and what the corresponding lightface class is. See the companion paper [Reference Day, Greenberg, Harrison-Trainor and Turetsky8] for further details. We further remark that the new system of descriptions of Borel Wadge classes is further explored in [Reference Greenberg and Turetsky17], where the authors give a new characterisation of the reduction property for these classes.
4.1 Reverse mathematics
As mentioned in the introduction, the proofs we gave are sufficiently effective so that they can be made within the system
![]() $\mathsf {ATR}_0$
of reverse mathematics. This is in some sense the weakest system which allows a meaningful development of Borel sets [Reference Simpson53, Chapter V]. The main point is that the true stages machinery is effective, and so can be defined in
$\mathsf {ATR}_0$
of reverse mathematics. This is in some sense the weakest system which allows a meaningful development of Borel sets [Reference Simpson53, Chapter V]. The main point is that the true stages machinery is effective, and so can be defined in
![]() $\mathsf {ATR}_0$
and all of its properties are provable in
$\mathsf {ATR}_0$
and all of its properties are provable in
![]() $\mathsf {ATR}_0$
. Thus:
$\mathsf {ATR}_0$
. Thus:
Theorem 4.4. Louveau’s separation theorem (Theorem 4.3) is provable in
![]() $\mathsf {ATR}_0$
.
$\mathsf {ATR}_0$
.
We remark that in contrast, Louveau’s original proof in [Reference Louveau35], which is the proof which appears in standard texts such as [Reference Sacks49] or [Reference Miller42], appears to require the stronger system
![]() $\Pi ^1_1\text {-}\mathsf {CA}_0$
.
$\Pi ^1_1\text {-}\mathsf {CA}_0$
.