Michael Darwin Morley, aged 90, Emeritus Professor of Mathematics at Cornell University, passed away October 12, 2020. Morley’s groundbreaking 1965 paper Categoricity in Power was the beginning of modern model theory and laid the foundation for decades of future developments.
Morley was born September 29, 1930 in Youngstown, Ohio and received his B.S. degree in mathematics from Case Institute of Technology in 1951. In 1952, he began graduate work at the University of Chicago joining an energetic group of young logicians including William Howard, John Myhill, Anil Nerode, Raymond Smullyan, Stanley Tennenbaum, and the undergraduate Paul Cohen. While at the University of Chicago he met his future wife Vivienne Brenner, a fellow graduate student who finished her thesis on singular integrals under Antoni Zygmund in 1956. They were a devoted couple for over 50 years.
Saunders Mac Lane served as his formal advisor at the University of Chicago. Mac Lane refused to grant a Ph.D. for Morley’s early work on saturated models, but helped arrange for Morley’s employment from 1955 to 1961 at the University of Chicago’s Laboratory for Applied Sciences, where he considered military applications of mathematics.
Much of Morley’s work on saturated models was discovered independently by Robert Vaught and Morley left Chicago in 1961 to work with Vaught at Berkeley, first as a visiting graduate student and later as an Instructor. Together they published their independent development of saturated models in [Reference Morley and Vaught26]. This paper built on Barni Jónsson’s development of the notion of uncountable universal-homogeneous models in universal algebra. Its innovations included a) replacing substructure with elementary substructure, and thus universally axiomatizable theories with first order theories, b) introducing special models so as to avoid the reliance on using the GCH (introduced by Hausdorff) to study universal models, and c) the general proof of the uniqueness of saturated models in a given regular cardinality.
Categoricity in Power
While at Berkeley, Morley laid the foundation for modern model theory in his proof of Łos’ conjecture on categoricity in power for countable languages: a first order theory in a countable language is
![]() $\aleph _1$
-categorical if and only if it is
$\aleph _1$
-categorical if and only if it is
![]() $\kappa $
-categorical for all uncountable cardinals
$\kappa $
-categorical for all uncountable cardinals
![]() $\kappa $
. One of Morley’s key insights was the importance of the topology of type spaces in understanding the properties of theories. Inspired by his study at the University of Chicago with Marshall Stone, Morley introduced the notion of a totally transcendental theory, the first general stability theoretic condition with a wide range of consequences. A theory T is totally transcendental if the Cantor–Bendixson derivative of the Stone space of types over a saturated model vanishes at some stage
$\kappa $
. One of Morley’s key insights was the importance of the topology of type spaces in understanding the properties of theories. Inspired by his study at the University of Chicago with Marshall Stone, Morley introduced the notion of a totally transcendental theory, the first general stability theoretic condition with a wide range of consequences. A theory T is totally transcendental if the Cantor–Bendixson derivative of the Stone space of types over a saturated model vanishes at some stage
![]() $\alpha _T$
. That is, every complete type has an ordinal ‘Morley rank’. A second key insight was the importance and power of indiscernibles. His proof proceeds by an original application of Ehrenfeucht–Mostowski models to prove an
$\alpha _T$
. That is, every complete type has an ordinal ‘Morley rank’. A second key insight was the importance and power of indiscernibles. His proof proceeds by an original application of Ehrenfeucht–Mostowski models to prove an
![]() $\aleph _1$
-categorical theory is totally transcendental. By a, now familiar to model theorists, tree argument he showed that totally transcendental theories in a countable language are
$\aleph _1$
-categorical theory is totally transcendental. By a, now familiar to model theorists, tree argument he showed that totally transcendental theories in a countable language are
![]() $\kappa $
-stable for all cardinals
$\kappa $
-stable for all cardinals
![]() $\kappa $
and hence have saturated models of cardinality
$\kappa $
and hence have saturated models of cardinality
![]() $\kappa $
for all cardinals
$\kappa $
for all cardinals
![]() $\kappa $
.Footnote
1
He generalized Vaught’s work on prime models for a theory to ‘prime models over a set’ and proved a totally transcendental theory has prime models over every set. Moreover, if
$\kappa $
.Footnote
1
He generalized Vaught’s work on prime models for a theory to ‘prime models over a set’ and proved a totally transcendental theory has prime models over every set. Moreover, if
![]() $A_i$
for
$A_i$
for
![]() $i<\gamma $
is a continuous chain of subsets of a model and
$i<\gamma $
is a continuous chain of subsets of a model and
![]() $B_i$
is prime over
$B_i$
is prime over
![]() $A_i$
for
$A_i$
for
![]() $i<\delta $
, then for limit
$i<\delta $
, then for limit
![]() $\delta $
,
$\delta $
,
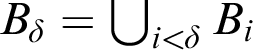 $B_{\delta } = \bigcup _{i<\delta } B_i$
. Considering extensions of types with minimal Morley rank, he showed any model of a totally transcendental theory contains an infinite set of indiscernibles over an arbitrary subset with smaller cardinality. Combining these last two methods, he concluded that if a totally transcendental theory has some uncountable model that is not saturated, it has a non-saturated model in any uncountable
$B_{\delta } = \bigcup _{i<\delta } B_i$
. Considering extensions of types with minimal Morley rank, he showed any model of a totally transcendental theory contains an infinite set of indiscernibles over an arbitrary subset with smaller cardinality. Combining these last two methods, he concluded that if a totally transcendental theory has some uncountable model that is not saturated, it has a non-saturated model in any uncountable
![]() $\kappa $
. The theorem then follows from the uniqueness of saturated models. This work was the core of his 1962 University of Chicago Ph.D. thesis. While Mac Lane remained his nominal thesis advisor, Morley would later say that his dissertation was ‘written under the supervision of Professor Robert Vaught’. The results of his thesis were announced in the Proceeding of the National Academy of Science [Reference Morley17] and published in the seminal paper Categoricity in Power [Reference Morley18].
$\kappa $
. The theorem then follows from the uniqueness of saturated models. This work was the core of his 1962 University of Chicago Ph.D. thesis. While Mac Lane remained his nominal thesis advisor, Morley would later say that his dissertation was ‘written under the supervision of Professor Robert Vaught’. The results of his thesis were announced in the Proceeding of the National Academy of Science [Reference Morley17] and published in the seminal paper Categoricity in Power [Reference Morley18].
Morley’s thesis closed with seven provocative questions that stimulated the subsequent development of model theory. The first two concern
![]() $\aleph _1$
but not
$\aleph _1$
but not
![]() $\aleph _0$
-categorical theories. Morley partially answers the first in [Reference Morley20] proving that the countable models can be arranged in a chain of length at most
$\aleph _0$
-categorical theories. Morley partially answers the first in [Reference Morley20] proving that the countable models can be arranged in a chain of length at most
![]() $\omega $
. Baldwin and Lachlan [Reference Baldwin and Lachlan2] showed non-trivial finite chains are impossible. Extensions of this result to superstable, supersimple, … have continued for more than half a century. Baldwin and Lachlan [Reference Baldwin and Lachlan2] also give an alternative proof of the categoricity theorem by showing that a theory in a countable language is
$\omega $
. Baldwin and Lachlan [Reference Baldwin and Lachlan2] showed non-trivial finite chains are impossible. Extensions of this result to superstable, supersimple, … have continued for more than half a century. Baldwin and Lachlan [Reference Baldwin and Lachlan2] also give an alternative proof of the categoricity theorem by showing that a theory in a countable language is
![]() $\kappa $
-categorical if and only if it is totally transcendental and has no Vaughtian pairs. Their proof focused attention on definable sets of Morley rank and degree 1, dubbed strongly minimal in [Reference Marsh16] (a Dartmouth thesis supervised informally by Morley). Morley’s genius was illustrated by the return to his proof to show categoricity transfer in continuous logic [Reference Baldwin and Lachlan3, Reference Shelah and Usvyatsov33] while the strongly minimal approach fails [Reference Hanson8, Reference Noquez27].
$\kappa $
-categorical if and only if it is totally transcendental and has no Vaughtian pairs. Their proof focused attention on definable sets of Morley rank and degree 1, dubbed strongly minimal in [Reference Marsh16] (a Dartmouth thesis supervised informally by Morley). Morley’s genius was illustrated by the return to his proof to show categoricity transfer in continuous logic [Reference Baldwin and Lachlan3, Reference Shelah and Usvyatsov33] while the strongly minimal approach fails [Reference Hanson8, Reference Noquez27].
The second question asked whether an
![]() $\aleph _1$
-but not
$\aleph _1$
-but not
![]() $\aleph _0$
categorical theory can be finitely axiomatizable. Peretyatkin [Reference Peretyatkin28] answered yes 15 years later.Footnote
2
Presciently, Morley did not raise in print the question for theories categorical in all infinite powers. The proof that no totally categorical theory is finitely axiomatizable [Reference Cherlin, Harrington and Lachlan7, Reference Zilber34, Reference Zilber35] led to the development of geometric stability theory.
$\aleph _0$
categorical theory can be finitely axiomatizable. Peretyatkin [Reference Peretyatkin28] answered yes 15 years later.Footnote
2
Presciently, Morley did not raise in print the question for theories categorical in all infinite powers. The proof that no totally categorical theory is finitely axiomatizable [Reference Cherlin, Harrington and Lachlan7, Reference Zilber34, Reference Zilber35] led to the development of geometric stability theory.
The third question was to generalize the Łos conjecture to uncountable languages. In order to solve this problem, Saharon Shelah began his deep development of stability theory and classification theory. In particular, Shelah showed that for an uncountable language L categoricity in a
![]() $\kappa>|L|$
implies superstability but not total transcendence.
$\kappa>|L|$
implies superstability but not total transcendence.
The fourth asked whether it was possible for a first order theory in an uncountable language to be
![]() $\kappa $
-categorial but only have models with cardinality
$\kappa $
-categorial but only have models with cardinality
![]() $\geq \kappa $
. This was shown impossible for various cases by Keisler and Shelah and in general [Reference Shelah31, IX.1.19]. Question 5 was a bit technical and answered by Jack Silver before publication.
$\geq \kappa $
. This was shown impossible for various cases by Keisler and Shelah and in general [Reference Shelah31, IX.1.19]. Question 5 was a bit technical and answered by Jack Silver before publication.
Questions 6 and 7 concerned the value of the bound
![]() $\alpha _T$
on Morley rank. Morley proved in the paper the bound was countable for countable totally transcendental theories and asked if it was finite for
$\alpha _T$
on Morley rank. Morley proved in the paper the bound was countable for countable totally transcendental theories and asked if it was finite for
![]() $\aleph _1$
-categorical theories. Using a slightly different rank Baldwin answered this positively in [Reference Baldwin1].
$\aleph _1$
-categorical theories. Using a slightly different rank Baldwin answered this positively in [Reference Baldwin1].
But perhaps the most influential of Morley’s conjectures is one he apparently didn’t publish: the number of models with power
![]() $\kappa $
of a first order theory is non-decreasing as a function of the cardinal
$\kappa $
of a first order theory is non-decreasing as a function of the cardinal
![]() $\kappa $
for uncountable
$\kappa $
for uncountable
![]() $\kappa $
. It was widely circulated as Morley’s conjecture by the late 1960s. Shelah solved this problem by listing the possible spectrum functions
$\kappa $
. It was widely circulated as Morley’s conjecture by the late 1960s. Shelah solved this problem by listing the possible spectrum functions
![]() $I_T(\kappa )$
, the number of models of T of cardinality
$I_T(\kappa )$
, the number of models of T of cardinality
![]() $\kappa $
, and noting that all were non-decreasing on uncountable cardinals. Morley and Keisler [Reference Keisler and Morley11] made progress on this question for homogenous models under GCH. Full clarification appeared in [Reference Hart, Hrushovski and Laskowski10, Reference Shelah31, Reference Shelah32]. The closest to sort of inductive proof that Morley probably envisioned is [Reference Hart9] but it also relies on Shelah’s case distinction.
$\kappa $
, and noting that all were non-decreasing on uncountable cardinals. Morley and Keisler [Reference Keisler and Morley11] made progress on this question for homogenous models under GCH. Full clarification appeared in [Reference Hart, Hrushovski and Laskowski10, Reference Shelah31, Reference Shelah32]. The closest to sort of inductive proof that Morley probably envisioned is [Reference Hart9] but it also relies on Shelah’s case distinction.
Although Morley was not motivated by applications, his work soon had an impact on model theoretic algebra. The significance of Morley’s topological approach to rank was emphasized when Berline [Reference Berline4] proved that for algebraically closed fields Morley ranks is the same as Krull dimension. Blum [Reference Blum5] gave a natural axiomatization of the theory of existentially closed differential fields of characteristic 0 and showed it is totally transcendental. Morley’s existence theorem for prime model extensions immediately implied the existence of differential closures and later analysis of Shelah [Reference Shelah30] implied uniqueness. Morley rank provides a useful notion of dimension in differential algebra though subtle but significant differences have arisen between model theoretic and algebraic ranks in the study of differential fields [Reference Pong29]. Macintyre [Reference Macintyre13, Reference Macintyre14] began the study of algebra under stability theoretic hypotheses by classifying
![]() $\aleph _1$
-categorical groups and fields; in particular proving that an infinite totally transcendental field is algebraically closed.
$\aleph _1$
-categorical groups and fields; in particular proving that an infinite totally transcendental field is algebraically closed.
After Categoricity in Power
In 1963 Morley left Berkeley to become an Assistant Professor at University of Wisconsin. Although Morley wrote fewer than a dozen further research papers, they include many of the formative results of the subject.
Morley continued his innovations in the use of indiscernibles. He pioneered the use of the partition calculus, particularly the Erdös–Rado Theorem, to build large models by stretching subtlety chosen sequences of indiscernibles establishing Löwenheim-Skolem properties for (pairs of) cardinals. As Morley made clear these methods could interpreted in terms of ‘Hanf numbers’ (If there is a model with property P of cardinality
![]() $H(P)$
, there are arbitrarily large such models.). These results [Reference Morley19, Reference Morley23] were rendered into a beautiful lecture series which was written up by Vivienne Morley [Reference Morley21, Reference Morley25]. These Hanf numbers have two interpretations: ‘a type can be omitted in a model of cardinality
$H(P)$
, there are arbitrarily large such models.). These results [Reference Morley19, Reference Morley23] were rendered into a beautiful lecture series which was written up by Vivienne Morley [Reference Morley21, Reference Morley25]. These Hanf numbers have two interpretations: ‘a type can be omitted in a model of cardinality
![]() $\kappa $
’ or ‘a sentence in an infinitary language has a model of cardinality
$\kappa $
’ or ‘a sentence in an infinitary language has a model of cardinality
![]() $\kappa $
’. This tool is fundamental in the contemporary study of infinitary logic and abstract elementary classes.
$\kappa $
’. This tool is fundamental in the contemporary study of infinitary logic and abstract elementary classes.
While at Wisconsin, he collaborated fruitfully with Keisler. In addition to the work on spectrum functions mentioned above, Keisler and Morley established the foundational results on nonstandard models of set theory. They [Reference Keisler and Morley12] proved that if N is a countable model of ZFC, for any regular cardinal
![]() $\kappa $
of N there is an elementary extension
$\kappa $
of N there is an elementary extension
![]() $N'$
of N which adds no new elements to
$N'$
of N which adds no new elements to
![]() $\kappa $
. Curiously, they observe that this theorem holds for Bernays–Morse set theory but not for Bernays–Gödel set theory.
$\kappa $
. Curiously, they observe that this theorem holds for Bernays–Morse set theory but not for Bernays–Gödel set theory.
Morley became an Associate Professor at Cornell University in 1967 and was promoted to Professor in 1970. Again exploiting the topology of type space and spaces of countable models, Morley [Reference Morley22] made what remains the strongest general progress toward Vaught’s conjecture that a countable complete first theory has either
![]() $\aleph _0$
or
$\aleph _0$
or
![]() $2^{\aleph _0}$
countable models. He proved that for a countable first order theory, or indeed an arbitrary sentences of
$2^{\aleph _0}$
countable models. He proved that for a countable first order theory, or indeed an arbitrary sentences of
![]() $L_{\omega _1,\omega }$
, if there are fewer than
$L_{\omega _1,\omega }$
, if there are fewer than
![]() $2^{\aleph _0}$
non-isomorphic countable models, then there are at most
$2^{\aleph _0}$
non-isomorphic countable models, then there are at most
![]() $\aleph _1$
. The key classical descriptive set theoretic fact Morley used in the proof is that an uncountable
$\aleph _1$
. The key classical descriptive set theoretic fact Morley used in the proof is that an uncountable
![]() $\boldsymbol {\Sigma }^1_1$
set has a nonempty perfect subset. Morley proved that the equivalence relation of isomorphism on the space of countable models has at most
$\boldsymbol {\Sigma }^1_1$
set has a nonempty perfect subset. Morley proved that the equivalence relation of isomorphism on the space of countable models has at most
![]() $\aleph _1$
or exactly
$\aleph _1$
or exactly
![]() $2^{\aleph _0}$
equivalence classes. This result foreshadowed John Burgess’ theorem [Reference Burgess6] that any
$2^{\aleph _0}$
equivalence classes. This result foreshadowed John Burgess’ theorem [Reference Burgess6] that any
![]() $\boldsymbol {\Sigma }^1_1$
equivalence relation with at least
$\boldsymbol {\Sigma }^1_1$
equivalence relation with at least
![]() $\aleph _2$
classes has a perfect set of inequivalent elements.
$\aleph _2$
classes has a perfect set of inequivalent elements.
Morley’s paper [Reference Morley24] stands as one of the founding papers of computable model theory. He characterized when a complete decidable theory T has a decidable saturated model, showing this happens exactly if there is a computable list of all types over
![]() $\emptyset $
. This is one of the first uses of a priority argument in a model theoretic setting.
$\emptyset $
. This is one of the first uses of a priority argument in a model theoretic setting.
Morley had four Ph.D. students, all of whom were women. His student Bonnie Gold reports, ‘I do know that Michael really admired and respected bright women in a way that was very unusual for the times (perhaps coming from his respect for his mother, originally, and then from his relationship with Vivienne)’. The four were: Charlotte Chell (1969) at the University of Wisconsin and Bonnie Gold (1976), Kay Wagner (1979) and Leena Reissell (1987) at Cornell.
Sometime during the flower-child years, Morley sent off for a mail-order minister’s license, and performed marriage ceremonies for a number of friends and colleagues – including his student Bonnie Gold with her second husband and his longtime friend and colleague Anil Nerode with his second wife. He was quite proud of the fact that no one whom he had married had gotten divorced. He was always willing to follow whatever ritual the celebrants wanted to have, as long as it didn”t require him to be a clergyman in a particular church. Although, when one couple married for tax purposes, Morley expressed his personal religious belief that paying extra taxes was a sin.
Morley retired from Cornell and became Professor Emeritus in 2003. Michael’s wife Vivienne was his constant companion from graduate school until her death in 2013. Morley was President of the Association for Symbolic Logic 1989–1991. During his more than 30 years at Cornell many students knew him as ‘Uncle Mike’, an empathetic adviser. His motto was ‘At Cornell, we like students’.
In 2003 Morley was awarded the Leroy P. Steele Prize of the American Mathematical Society for Seminal Contribution to Research for this paper. The citation says that he ‘…set in motion an extensive development of pure model theory by proving the first deep theorem in this subject and introducing in the process completely new tools to analyze theories and their models’. We have attempted to trace some the details of these tools and then their long term impact on mathematical logic. In addition to his trailblazing mathematical work, Morley was known for his generosity, kindness and an infectious sense of humor.



